某水电站辉绿岩卸围压三轴流变试验应力应变关系分析

杨代六，贺如平

(中国水电顾问集团成都勘测设计研究院 科学研究所，四川成都 610072)

岩石的流变特性是影响水电工程围岩稳定性的重要因素之一。众所周知，岩体工程一般处于复杂的应力状态中，仅由单一应力路径和简单受力状态下的流变研究不能全面反映实际工程的加、卸荷受力状态，因此，有必要开展复杂应力路径下的流变试验研究。限于种种原因，对于恒定轴向应力、逐级减小围压条件下的三轴蠕变试验研究目前还不多见。

在卸围压的试验中，所采用的加载方式一般描述为“采用恒定轴压分级卸除围压的加载方式”。此处的“围压”指最小主应力σ3。而“轴压”在不同的文献中有不同的定义，有的指轴向的最大主应力σ1;有的指试验机的轴向输出力P，即σ1-σ3［1］。

表面上看这两种方式都是保持“轴压”不变卸围压，但实际上两者规律并不相同。为此，笔者以大岗山水电工程为依托，采用以下两种应力路径进行了卸围压流变试验:①保持σ1-σ3不变，逐级卸围压;②保持σ1不变，逐级卸围压，以求找出其内在的规律。

1 试验方法

1.1 试验条件

试件为自然风干、加工精度满足试验规程要求的辉绿岩标准圆柱体。试验在岩石全自动流变仪上进行。

1.2 流变试验方案设计

(1)σ1恒定，分级卸围压。

1#岩样在轴向应力σ1为180 MPa，围压σ3为40 MPa 的条件下开始分级卸载。此次试验采用的应力路径见图1、表1。

图1 σ1恒定，卸围压试验应力路径示意图

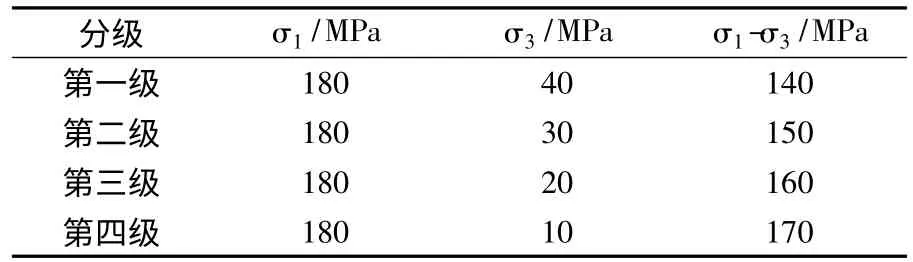
表1 σ1恒定，分级卸围压应力路径表

(2)σ1-σ3恒定，分级卸围压。

2#岩样在轴向应力σ1-σ3为140 MPa，围压σ3为40 MPa 的条件下开始分级卸载。此次试验采用的应力路径见图2、表2。

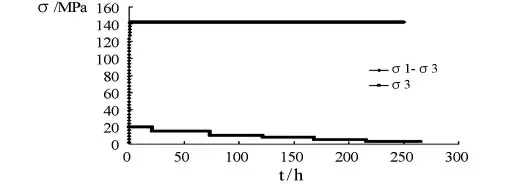
图2 σ1-σ3恒定，分级卸围压应力路径示意图

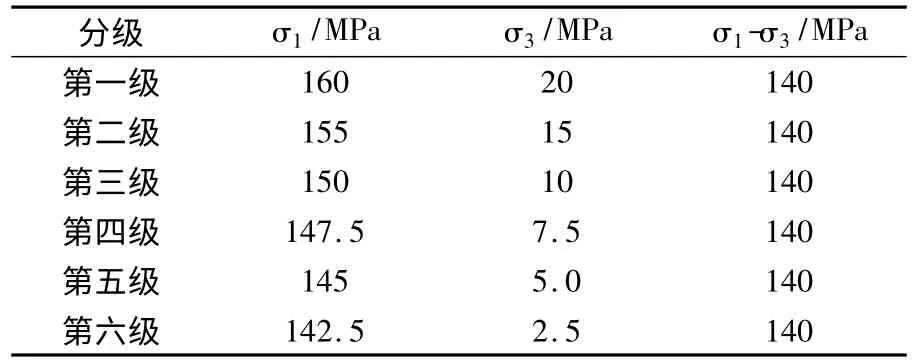
表2 σ1-σ3恒定，分级卸围压应力路径表

2 试验结果

2.1 σ1不变，分级卸围压

假设卸载初期的变形为弹性变形，用线弹性力学理论初步分析卸围压过程中轴向应变和横向应变的变化规律。

由广义胡克定律可知:

在试验中，保持σ1不变，且σ1=σ3，因此将式(1)、(2)表示为增量形式，则:

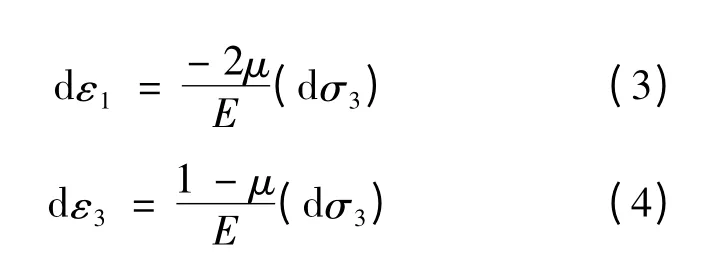
随着围压σ3的减小，轴向应变增大(压缩)，横向应变减小(膨胀)。

图3、4为轴向应变、横向应变～时间曲线。由图可见试验曲线与前面的分析结果一致:在卸围压过程中，轴向应变向轴向压缩方向变大，横向应变向侧向膨胀方向变大。

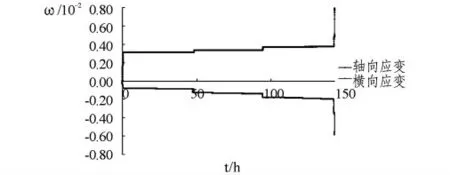
图3 σ1恒定，分级卸围压应变～时间曲线图

图5为σ1恒定，分级卸围压流变试验的偏应力～应变曲线。与围压不变、加载轴压的三轴流变试验不同，该卸围压试验从围压卸载开始就表现出明显的扩容。分析其原因，主要是因为卸围压情况下，相当于在原有应力之上叠加一个拉应力，极易造成沿σ1方向的张性裂隙张开，在长时间的流变损伤状态下裂纹会逐渐扩展，其宏观表现即为蠕变变形并以稳定速度增长。

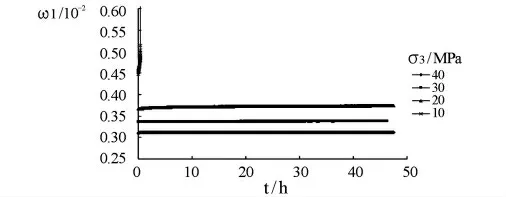
图4 σ1恒定，分级卸围压轴向应变～时间分级曲线示意图

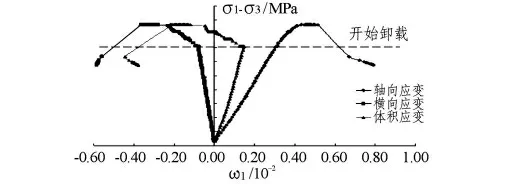
图5 σ1恒定，分级卸围压应力-应变曲线示意图

图6为σ1恒定，分级卸围压流变试验的围压～应变曲线。由其可以直观地看到:随着围压的减小，轴向应变逐步减小(压缩)，横向应变逐步减小(膨胀)。横向应变的变化速率大于轴向，从而导致宏观上岩样的扩容，当应变增大到一定值后，变形速率突然增大(曲线上的近似直线段)，变形急剧增加，试样产生破坏。

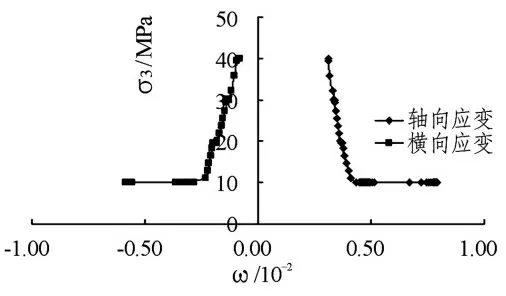
图6 σ1恒定，分级卸围压围压～应变曲线示意图

2.2 σ1-σ3不变，分级卸围压

同样假设卸载初期的变形为弹性变形，用线弹性力学理论初步分析卸围压过程中轴向应变和横向应变的变化规律。

由广义胡克定律可知:

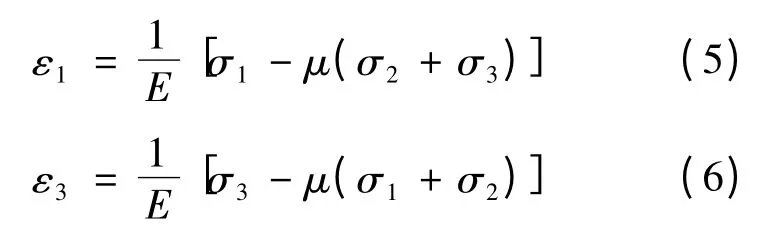
在试验中，保持σ1—σ3=△σ不变，且σ2+σ3。因此将式(5)、(6)表示为增量形式，则:

随着围压σ3的减小，轴向应变减小(伸长)，横向应变减小(膨胀)。

与σ1恒定，分级卸围压的结果不同，横向应变变化规律相同，都是横向膨胀，但轴向应变规律则完全相反。σ1恒定时，轴向应变压缩;而σ1-σ3恒定时，轴向应变则伸长。

由图7、8中的应变～时间曲线可知，卸围压初期横向应变就表现出明显的流变特征且横向膨胀，与前面的分析规律相同。而轴向应变在卸载初期变形量很小，在围压15 MPa 和10 MPa 时，轴向应变变小，即轴向伸长，这与前面基于线弹性理论的分析规律一致;而当围压小于7.5 MPa 时，轴向应变规律出现了变化，开始由轴向伸长变为轴向压缩，并且出现明显的蠕变现象，直至最终试件破裂。

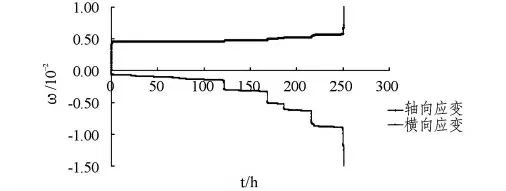
图7 σ1-σ3恒定，分级卸围压应变-时间曲线示意图

图8 σ1-σ3恒定，分级卸围压轴向应变-分级时间曲线示意图

分析其产生的原因可知:在卸围压前期，可以近似地认为岩样处于弹性变形的范畴，随着卸围压的进行，岩石内部微裂隙不断扩展贯通，当损伤发展到一定程度将出现不可逆的塑性变形，这时，弹性理论已经不适用，岩体变形逐渐由弹性变形转变为塑性变形。

图9为σ1-σ3恒定，分级卸围压流变的应力～应变曲线。在卸围压过程中，横向应变变化十分明显，而轴向应变则相对较小。在卸围压一开始岩样即产生体积扩容。

图9 σ1-σ3恒定，分级卸围压应力-应变曲线示意图

图10为σ1-σ3恒定，分级卸围压流变的围压～应变曲线。由图10可见，横向应变在卸围压过程中自始至终都是逐渐减小的，即表示岩样始终是横向膨胀的;而轴向应变开始先是有微小的减小，经过一定时间以后才转为增大，即表示岩样先是有微小伸长，随着围压降低到一定程度才转变为轴向压缩。当应变增大到一定程度后，既使围压保持不变，变形仍急剧增大，图10中表现为水平线，岩样宏观破坏。

图10 σ1-σ3恒定，分级卸围压围压-应变曲线示意图

3 比较分析

3.1 试验曲线分析

综上可知，σ1恒定和σ1-σ3恒定，卸围压的流变试验规律并不完全相同，其横向变形均表现为侧向膨胀，但轴向变形却比较复杂。σ1恒定卸围压时，轴向变形一直为轴向伸长;σ1-σ3恒定卸围压时，轴向变形先是有微小伸长，然后再逐渐转变为轴向压缩。

σ1恒定卸围压时，轴向变形一直增大，没有转折点，规律明显，比较适合于研究岩石的卸荷流变性质;σ1-σ3恒定卸围压时，轴向变形有转折点，可以以此区分其弹性变形和塑性变形的临界应力点。

3.2 屈服接近度分析

屈服接近度可以表述为:描述一点的现时状态与相对最安全状态的参量比YAIε［0，1］，YAI=0时应力点在屈服面上，发生屈服;YAI=1时应力点在等倾线上，处于相对最安全状态［2］。基于Mohr-Coulomb 准则的屈服接近度为:

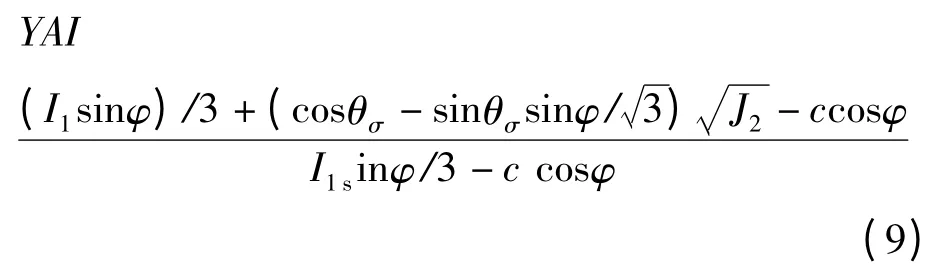
式中 I1为应力张量的第一不变量;J2为偏应力张量的第二不变量;θσ为应力洛德角;c 为凝聚力;φ为摩擦角。

图11为两种加载路径下的屈服接近度比较，由图可知:两种方式下，屈服接近度YAI 均随围压的减小而减小，即越来越接近于屈服面。而在同等围压情况下，σ1恒定卸围压的YAI 要小于σ1-σ3恒定的情况，说明σ1恒定卸围压路径的加载方式能更快的导致岩样破坏。

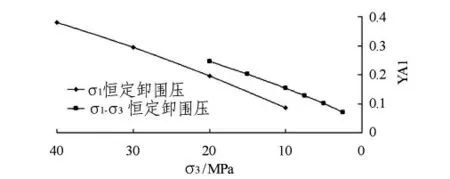
图11 两种应力路径下的试验数据屈服接近度比较示意图

为了更准确地说明这一点，可以假设对同一岩样进行两种加载方式下的YAI 分析，以消除不同岩样的差异性。表3为两种加载路径下的应力分级。由表3可见，两种工况的初始应力状态完全一样，一种保持σ1不变进行卸围压，另一种则保持σ1-σ3不变。

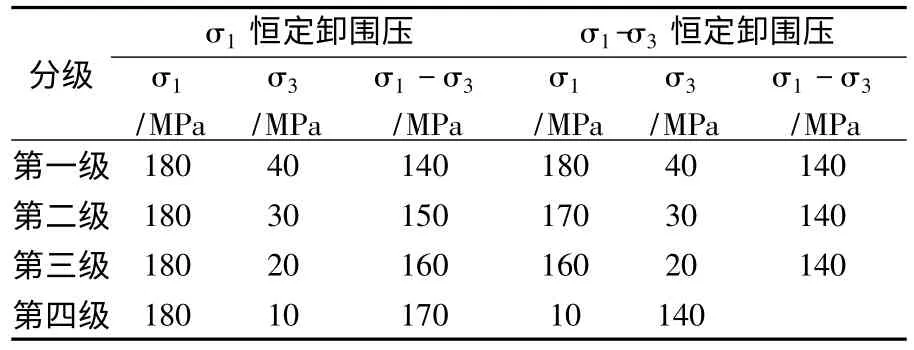
表3 σ1恒定，分级卸围压的应力路径表

图12 两种加载路径下的屈服接近度分析示意图

由图12可见，保持σ1不变情况的屈服接近度YAI 在卸围压过程中比保持σ1-σ3不变时下降更快，说明σ1恒定卸围压路径的加载方式能更快的导致岩样屈服破坏。

4 结语

(1)进行了σ1恒定卸围压和σ1-σ3恒定卸围压流变试验，分析了两种不同应力路径下辉绿岩的流变变形特征。两种方式下，在卸围压过程中，岩样的横向变形均表现为侧向膨胀，但轴向变形规律并不相同:σ1恒定时，轴向变形一直表现为轴向压缩，σ1-σ3恒定时，先是有微小伸长，再逐渐转变为轴向压缩。这与两种方式加载路径有关，同时也说明在卸围压过程中，岩体变形逐渐由弹性向塑性转变。

(2)与三轴压缩蠕变破坏方式不同，卸围压流变试验从卸载一开始，岩样就表现为体积扩容，这与卸围压试验更容易引起平行于轴向的裂纹扩展有关。

(3)通过屈服接近度的概念，可以很好的评价卸围压流变过程中岩样整体的应力强度和接近屈服破坏的程度。

［1］王芝银，李云鹏.岩体流变理论及其数值模拟［M］.北京:科学出版社，2008.

［2］周辉，张传庆，冯夏庭，等.隧道及地下工程围岩的屈服接近度分析［J］.岩石力学与工程学报，2005，24(17):3083-3087.