孤子精确求解方法浅论
新乡学院物理系 陈泽章
在线性理论日臻完善的今天,非线性科学已经成为了各个研究领域的研究焦点[1]。在非线性科学中,孤立子理论有着非常重要的位置。它在量子场论、粒子物理、凝聚态物理、流体物理、等离子体物理和非线性光学等物理学的各个分支及数学、生物学、化学,通信等各自然科学领域得到了广泛的应用,也极大地促进了一些相关数学理论的发展,因此引起了科研者对可积系统研究的极大兴趣。
1.孤立波和孤立子
1834年,从爱丁堡到格拉斯哥的运河里一只正在行驶的船突然停止了前进,这时英国科学家Russell恰好观察到运河中被船推动的水并没有停止,反而以汹涌翻腾的状态聚集在船头,接着便以巨大的速度滚滚向前,且保持着巨大的轮廓分明的光顺孤立的峰状外形。他骑着马跟踪了一至两英里,在运河的拐弯处,这种孤立行进的水峰才终于消失。Russell认识到这种水波现象是具有关键性质的新现象、新事物,随后进行了更加细致的研究,在实验室作了很多实验,用多种方法激发,也观察到了同样的现象。他称这种波为孤立波(Solitary wavc)。然而由于受限于当时的数学理论和科学水平,Russell未能从流体力学出发给孤立波以合理的理论解释。
直到1895年,两位荷兰科学家科学家Kortweg与de Vries用一波动方程对孤立波现象进行完整的理论分析后,在长波近似和小振幅的假定下,建立了单向运动浅水波的非线性浅水波方程,即著名的KdV方程:

他们从方程中求出了与Russell描述一致的,即具有形状不变的脉冲状的孤立波解,从而在理论上证明了孤立波解的存在,孤立波的形成原因才得到了合理的理论解释[2]。然而,这种波是否稳定,两个波碰撞后是否变形?这些问题却长期没有得到解答。以至于有些人怀疑,既然方程(1)是非线性偏微分方程,解的叠加原理不再成立,碰撞后解的形状很可能破坏。持这种观点的人认为这种波不稳定,因而研究它没有什么物理意义,于是关于孤立波现象的研究与KdV方程又被默默地遗忘了几十年。
直到1955年,在美国阿尔莫斯国家实验室,著名物理学家费米(E.Fermi)、帕斯塔(J.Pasta)和乌莱姆(U.Slam)发现在流体力学以外的其他的物理领域中也存在象Rusell描述的这种孤立波,才又掀起了这一领域研究热潮。
为了从数值实验上验证统计力学中的能量均分定理,他们数值计算了用非线性弹簧联结的64个质点组成的弦的振动。按照能量均分原理,如果只对少数质点进行激发,由于弱的非线性相互作用,经长时间以后,初始的激发能量应有涨落地均衡的分布到每个质点。然而计算结果却大大出乎人的意料,长时间以后能量几乎全部回到了初始集中在少数质点上的状态。这个结果预示着这个非线性系统可以出现孤立波。这就是著名的FPU问题。随后1965年,美国数学家采布斯基(Zabusky)与克鲁思卡尔(Kruskal),从连续统一体的观点来考虑把FPU的非线性振子系统的能量不均分问题与KdV方程联系了起来。他们还是采用数值模拟的方法,对KdV方程两个波速不同的孤波解进行了研究。设有同向行进的两个孤立波,波幅较高在后的孤立波,逐渐赶上前面幅度较低的孤立波,令人惊奇的是两个孤立波相遇后并没有湮没,反而很好地分离开来并且仍然保持着各自原来的形状和速度继续前进。这说明孤立波不仅非常的稳定而且还具有类似粒子碰撞的不变性质。据此Kruskal和Zabusky便引入了“孤立子(Soliton)”概念来描述一个非线性方程或非线性体系的任意解,着此解满足:①可表示成一个固定形式的波;②是局部的、衰变的或在无穷大时变为常数;③可与其它的孤子进行强烈的相互作用,在相互作用后即使叠加原理成立其形式亦不会改变。此后人们发现,KdV方程在许多物理体系中都存在,并且除KdV方程外,其它的一些偏微分方程也有孤立波解,进一步说明孤立波是一种普遍存在的物理现象。
2.孤子精确解求解方法
到目前为止,我们可以常见的几种典型孤波方程包括KdV方程、Sine-Gordon(SG)方程、Nonlinear-SchrSdinger(NLS)方程以及这些方程的各种修正形式。其中,KdV方程主要应用于浅水波中的表面波、等离子体中的电磁波与声波、非简谐的晶格振动等物理领域。SG方程主要应用于晶格位错的传播、铁磁体中畴壁的运动、超导约瑟夫森结等领域.NLS方程主要应用在深水中的非线性波、电介质中强激光的自聚焦、超导等领域[3]。
孤立子理论的基础便是求解上述各种非线性偏微分方程。近年来,非线性数学物理领域取得了很大的成就,其中之一就是发展了求非线性方程精确解,特别是精确孤子解的各种有效方法。接下来我们便以KdV方程(1)为例,简要介绍几种孤子精确求解的方法。
2.1 逆散射变换(inverse sacttering transformation)方法
这种方法被人们广泛用来求解各类非线性系统的问题。其主要思路如下:首先对某个非线性偏微分方程引入一对相容的线性方程(又称Lax方程)

其中方程(2)是L的本征值方程,λ和 Ψ =Ψ ( x, t,λ)分别是L的本征值和本征函数。如果λ独立于时间t,相应的一对线性算子L和M(Lax对)满足的相容条件为:

然后求解与Lax方程(2)和(3)相对应的逆散射问题,得到含有散射数据的逆散射方程。在无反射条件下,由方程的约斯特(Jost)解获得孤子解.对于KDV方程(1),Lax对被选为

不同的非线性方程有不同的Lax对,它们满足的相容性条件是相应非线性方程的等价形式。这种方法在数学上具有很高的严性谨。将它用于许多非线性方程,都可得到单孤子、双孤子和多孤子解,是较经典的孤子理论之一。然而,这种方法思路较迂回曲折,且Lax对本身就很难求得,寻找方法并无规律可循。
2.2 Hirota方法.
Hirota方法的关键在于引进双线性算子(bilinear operator),将非线性方程简化为双线性形式,然后结合其它简单变换就可得到孤子解.例如,对KdV方程(1)引入合适的因变量变换将其带到方程(1),就得到相应的双线性方程


其中双线性算子被定义为
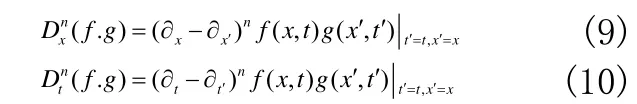
只要将φ按小量ε的幂级数展开,逐一求解各级方程,得到φ的级数解后,再代回(2.12)就可获得孤子解。Hirota方法思路清晰,数学方法相对简单,迄今为止,它已用于很多释非线性方程,获得各种孤子解,甚至包括一些特殊的孤子解。
这种方法是在寻找更多的非线性方程解的过程中发展来的.它主要包含两个方面的变换:不同方程之间的变换和同一方程不同解之间的变换。前者的关键是要找到非线性方程与相应的线性方程的backlund˙变换方程,再由已知线性方程的解求非线性方程的解;后者的关键是寻找非线性方程的两个解之间的backlund˙变换方程,由其中已知的解求未知的解。对于KdV方程(1),令xvψ=可将KdV方程化为:

若0v和v均是它的解,则可得到相应的backlund˙变换为:

[1]王明亮.非线性发展方程和孤立子[M].兰州:兰州大学出版社,1982.
[2]俞慧友.孤子理论及其在玻色爱因斯坦凝聚中的应用[D].长沙:湖南师范大学,2009.
[3]李彪.孤立子理论中若干精确求解方法的研究及应用[D].大连:大连理工大学,2004.

