WSN中基于RSSI的加权质心定位算法的改进

于慧霞

（南京邮电大学 南京 210046）

0 引言

在无线传感器网络中，按节点位置估测机制，根据是否依靠测量距离划分为基于测距(range-based)的算法和非基于测距(range-free)的算法。前者是利用测量得到的距离或角度信息来进行位置计算，而后者一般是利用节点的连通性和多跳路由信息交换等方法来估计节点间的距离或角度，并完成位置估算。

文献[6]提出了一种廉价实用的定位算法，该方法通过校正RSSI测距技术测量节点间的距离，并优选信标节点，最后用加权质心方法进行定位，该方法存在的缺点是在加权权重阶段没有对权值进行更好的选取；文献[7]提出了一种基于RSSI的修正加权质心定位算法，在该算法中采用测试距离倒数之和来代替距离和的倒数作为权重， 该算法对于质心算法的权值进行了很好的修正，但是在测距阶段没有充分考虑到信标节点的影响力，使得RSSI测距值存在着很大的误差。

本文融合文献[6]和文献[7]中算法的优点，并弥补两种算法中的不足，在基于校正RSSI测距的基础上，通过优选信标节点，最后采用修正加权权重的方法来对传统的质心定位算法进行改进。

1 算法模型

1.1 无线信号传播损耗模型

在基于接收信号强度指示RSSI的定位中，已知发射节点的发射信号强度，接收节点根据收到信号的强度，计算出信号的传播损耗，利用理论和经验模型将传输损耗转化为距离，再利用已有的算法计算出节点的位置。

一般地，在实际应用环境中，无线传感器网络模拟的传播模型我们考虑最多的就是综合性强并被广泛应用的Shadowing模型。

完整的Shadowing模型如下：

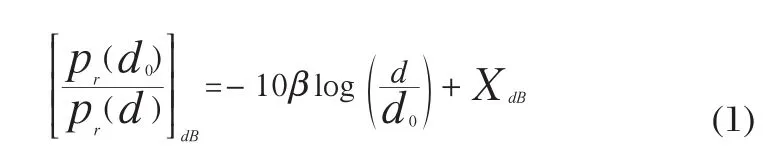
该模型包含两个部分，第一部分是路径损失模型（pass loss），它预测出当给定距离d0（一般取1 m）和接收信号强度pr(d0)作为参考时，距离d时的信号强度pr(d)。

其中，β是衰减指数，它通常是由场地测量得来的经验值，范围一般在2～6之间。障碍物越多相对数值越大。因此随着距离的增加接收到的平均能量下降的速度会越来越快。

Shadowing模型的第二部分XdB是一个对数正态的随机变量，它反映了当距离一定时，接收到能量变化。如果以dB作为计量单位时，它满足高斯分布。它是一个没有任何意义的高斯随机变量，它对Shadowing模型作了一个扩展，使之成为一个富有统计学的模型，本文出于环境复杂性的考虑，将使用Shadowing的完整模型，即将一个零均值高斯分布的随机噪声引入了无线电传播模型中，该噪声分布服从对数正态分布。

1.2 传统的质心定位算法模型

质心算法[3-4]是由南加州大学的Bulusu等人提出，在未知节点收到邻居信标节点的位置信息后，取这些邻居信标节点的质心作为该节点的估计位置。传统的质心算法（Centroid Algorithm）是一种基于连接性的，而无需距离信息的简单定位算法。传统的质心算法的基本原理如图1所示。

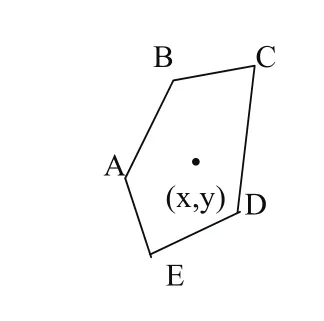
图1 质心定位算法的示意图

在质心算法中，信标节点周期性地向邻近节点广播信标分组，信标分组中包含信标节点的标识号和位置信息。当未知节点接收到来自不同信标节点的信标分组数量超过某一个门限或接收一定时间后，就确定自身位置为这些信标节点所组成的多边形的质心：为未知节点能够接收到其分组的信标节点坐标。

通过对无线电传播路径损耗模型的分析，可以发现普通质心算法没有反映出信标节点对节点位置的影响力大小，影响了定位精度。理论证明，利用节点之间的距离信息（接收信号强度指示RSSI），可获得定位信标节点的偏移权值，从而可以提高质心定位算法的精度。在基于RSSI的定位算法中，通常有普通的质心定位算法，加权质心定位算法、三角形面积定位算法等。这些模型中，普通的质心定位算法最简单，但定位精度较低，使用较少。一般来说，已知无线传感器网络的N个固定信标节点Bi的位置坐标（xi，yi），其中1≤i≤N，未知节点O的估计位置坐标为（x，y），那么基于RSSI的加权质心定位算法计算公式为：

其中，wi表示每个固定信标节点的权值，通常，该权值是未知节点到固定信标节点的距离函数的倒数。特殊情况下，如果未知节点不能与固定信标节点Bi通信，那么权值为零。

2 基于传统模型的改进算法模型

2.1 RSSI值校正模型-基于固定信标节点间距离的校正模型

如图2所示，假设o点是未知节点，Bi，Bj都是已知自身位置的锚节点。未知节点o到Bi的距离表示为doi，固定锚节点Bi和Bj之间的距离表示为dij.未知节点o接收到锚节点Bi信号的信号强度平均值为Poi（mW）。固定锚节点Bi接收到Bj的信号强度平均值（mW）为Pij，由上述式子（1）可知，它们之间存在着如下的关系：

又假设RSSI0i为未知节点A接收到锚节点Bi信号的RSSI平均值（dBm），RSSIij表示Bi接收到Bj信号的RSSI平均值（dBm）。因为在无线信道信号传播损耗模型中，信号强度平均值和RSSI信号平均值存在着如下关系（以图2为例）：

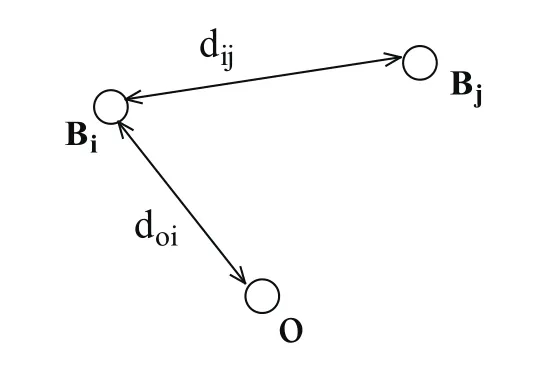
图2 基于RSSI的测距值校正模型

由上述分析可以得知：假设某个信标节点Bi的通信半径内有N个信标节点，我们在计算某个未知节点o到信标节点Bi的距离doi时，可以表示为所有的dij对于所有j的可能值的平均值，从而未知节点o到信标节点Bi的距离doi可以校正为如下式子：

2.2 修正权重的加权定位质心算法

根据上述提到的传统的加权质心定位算法的基本原理可知，加权权值这一部分对于整个算法定位精度有着至关重要的作用。加权质心定位算法中对于权值的选择，不同的文献采用不同的方式。本文中采取用文献[7]中距离倒数之和代替传统算法中距离和的倒数[5]的算法。

本文主要研究的基于RSSI的加权质心定位算法做法是：首先将所接收到的RSSI 数据转化为距离信息，将这些距离从小到大进行排序，并优选距离最小所对应的4个信标节点进行定位，每次取其中的3个信标节点进行组合，这样就会有4中不同的组合。然后分别以选取的3个信标节点为圆心，以未知节点到信标节点之间的距离为半径画圆，这样3个圆相交会产生公共的部分。此时，未知节点就应该位于所有圆的交集部分，以上述提到的质心算法为基础，对3个圆的共同交点组成的多边形进行分析，利用优选的锚节点和未知节点之间的距离为每一个坐标增加了权值，以体现不同顶点的贡献。算法的基本原理图如如图3所示。

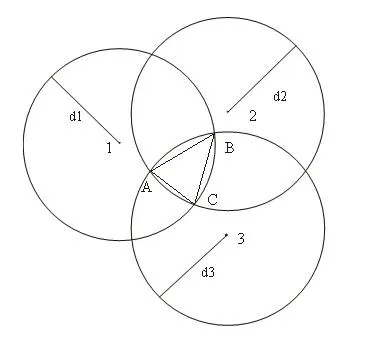
图3 本文提出的加权质心定位算法原理图

该加权定位算法中未知节点的估计坐标可以用以下公式来求取，即：

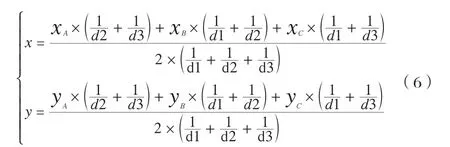
其中（x，y）就是未知节点的估计坐标，d1,d2,d3分别为未知节点获得的到3个信标节点的近似距离。（xA，yA），（xB，yB），（xC，yC）为利用上述算法原理求出的 3圆的交点位置坐标。

因此，本文所研究的基于RSSI值加权质心算法的基本思想是：在RSSI测距值的获取阶段，将信标节点之间的距离和信号强度信息同时考虑在内进行RSSI值校正；权值选择阶段采用了权值取距离倒数之和来对传统的加权质心算法进行融合改进。

2.3 算法步骤

锚节点周期性的以相同功率向周围广播信息，信息中包括自身节点ID及坐标，同时信标节点Bi将收到的信标节点Bj的RSSI值求均值，由式子（3）（4）（5）求出Pij和dij，并将结果广播出去。

未知节点在收到超过阈值N个信标信息后，停止接受信息。只记录同一个信标节点的RSSI均值。根据改进后的校正RSSI值测距算法，由式子（5）求出doi。

未知节点对计算得来的doi值从小到大排序，并建立RSSI值与节点到锚节点距离的映射。建立3个集合：

信标节点集合：Beacon={B1,B2,B3，…，BN}

信标节点位置信息集合：Position={(x1,y1), (x2,y2), (x3,y3),…，（xN,yN）}

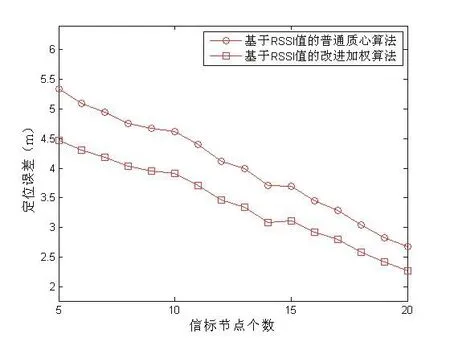
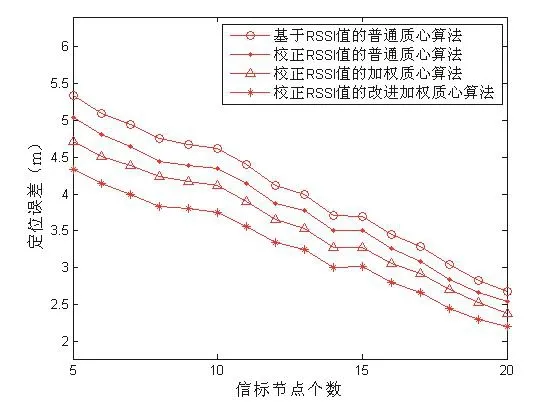
未知节点到信标节点距离集合Distance={do1,do2,do3,…，don}，do1

在上述集合中选取离未知节点距离最近的前4个信标节点进行定位，然后依照上述介绍的改进的加权质心定位算法，分别对4个定位点坐标进行计算。

最后取4个估计点组成的多边形的质心作为未知节点的坐标（x，y）。

3 仿真结果

为了对本文提出的RSSI测距值校正算法和修正加权质心算法进行验证，我们采用MATLAB对此进行仿真。仿真实验的初始条件为：无线传感器网络位于100 m×100 m的区域内，信标节点随机分布在此区域内，为了验证简单性，本文把未知节点初始化为原点（0,0）。无线信号载频为2.4 GHz，路径损耗系数设为4，节点的通信半径为50。另外，所有的仿真实验环境中都加入了均值为零，标准差为0.5的满足高斯分布的随机噪声，来代替实际环境中的反射、多径、物体移动、气候等带来的影响。在信标节点从5到25变化的基础上，我们分3个方面对本文提出的算法进行了仿真分析，仿真结果如图4-6所示，所有仿真次数都取500次，仿真结果取500次的平均值。

图4 信标节点个数变化时校正测距值对定位误差的影响

图5 信标节点个数变化时加权权值对定位误差的影响

图6 信标节点个数变化时融合两种算法后对定位误差的影响

上述中，图4验证了基于校正的RSSI算法的有效性，由图可以得知，相同条件下，信标节点个数从5到20时，定位算法的误差逐渐减小，说明增加信标节点的个数对于提高算法的定位精度有着重要作用。传统的RSSI定位算法经过RSSI测距值修正以后，定位误差减小，在20个信标节点定位的时候可以达到2.5m。图5验证了定位阶段中加权权重修正算法的有效性，可见经过权值修正后，改进后的算法相对于传统的RSSI质心定位算法有明显优势，这一部分说明了加权权重对于整个定位算法的重要作用。为了将RSSI测距修正和权值改进两种算法融合在一起，图6验证了基于RSSI校正的改进权重的加权质心定位算法的有效性。在信标节点为5时，该算法定位误差在4.4m左右，信标节点为20时，定位误差则在2.2m左右，由此可见，该融合算法相对于传统的基于RSSI的加权质心定位算法有着明显优势，大大的提高了算法的定位精度。

4 结论

加权质心定位算法采用了具有较大的无线发射功率的信标节点，其发射半径远大于普通节点的通信半径[8-10]，可以减少信标节点的数目，同时，该算法对于硬件的要求不高，具有较好的综合效果。本文算法在此基础上，研究了基于RSSI的加权质心定位算法，在基于测距阶段和加权定位阶段提出了新的改进算法，充分融合了rangebased与range-free两种算法的优点，使得改进后的算法定位精度得到了提高。另一方面，算法在信标节点的覆盖性问题和功率设计都有待进一步完善，在今后的应用中，可以通过硬件实验来验证算法的有效性。

[1]孙利民,李建中,陈渝,等.无线传感器网络[M].北京:清华大学出版社,2005.

[2]王福豹,史龙,任丰原.无线传感器网络的自身定位和算法[J].软件学报,2005,16(5):857-868.

[3]方震,赵湛,郭鹏,张卫国.基于RSSI测距分析[J].传感技术学报,2007,20(11):2526-2530.

[4]Li J,Li J,Cuo L,et al.Power-Efficient Node Localization Algorithm in Wireless Sensor Networks[C]//APWeb 2006 International Workshops, Harbin,China,2006,3842:420-430.

[5]陈维克,李文锋,首珩,等.基于RSSI的无线传感器网络加权质心定位算法[J].武汉理工大学学报,2006,30(12):265-268.

[6]赵昭,陈小惠.无线传感器网络中基于RSSI的改进定位算法[J].传感技术学报,2009(03).

[7]刘运杰,金明录,崔承毅.基于RSSI的无线传感器网络修正加权质心定位算法[J].传感技术学报,2010(05).

[8]Ssu K,Ou C,Jiau H C.Localization with Mobile Anchor Points in Wireless Sensor Networks[J].IEEE Transaction on Vehicular Technolo gy,2005,54(3):1187-1197.

[9]Bulusa N,Heidemann J,Estrin D.GPS-less Cost Outdoor Localization for Very Small Devices [J].IEEE Personal Communications Magazine,2000,7(5):28-34.

[10]文举,金建勋,袁海.一种无线传感器网络四边测距定位算法[J].传感器与微系统,2008,27(5):108-110.