基于RBF神经网络的雷达网抗干扰效果评估＊

胡 然 刘东玉 唐 忠 张金强

（中国人民解放军63892部队 洛阳 471003）

1 引言

雷达网是多部雷达的组合，它的抗干扰性能是衡量雷达网综合性能的一个很重要的指标，它的优劣直接关系到雷达网在实际的作战环境中能否将各种敌对干扰对其正常工作的影响减少到最小，从而较好地完成其情报信息提供任务［1～2］。雷达网是一个复杂的信息系统，影响其抗干扰性能的因素很多，其中既有可以定量表示的，也有只能定性说明的，并且这其中许多的因素对于雷达网综合抗干扰性能的影响也往往难于定量分析［3］。实际上由于诸因素集与综合评估指标集之间的关系是错综复杂的非线性关系，如果直接对抗干扰诸因素进行建模，进而得到一个完整准确的显形表示的这种映射关系评估模型通常有很大的困难［4～5］。

人工神经网络以独特的结构和处理信息的方法，使其近年来在智能控制、模式识别、故障判断、装备效能评估等许多实际应用领域取得了显著的成效。它是一个由许多人工神经元构成，模拟生物神经系统的网络系统，就学习、自适应和非线性大规模并行处理的能力。它对复杂非线性系统的处理方法和传统方法有很大的区别：网络通过自学习得到的东西，将其隐含在网络结构中，不需要对复杂系统的处理进行显示的定义［6～7］。采用RBF算法的人工神经网络具有良好的非线性映射能力，可为这一问题的解决提供新的途径。本文在分析研究雷达网抗干扰性能评估指标集的基础上，建立了具有客观性、敏感性和可测性的抗干扰评估指标体系，并提出一种基于神经网络的雷达抗干扰效果评估方法。

2 雷达网抗干扰效果评估指标体系

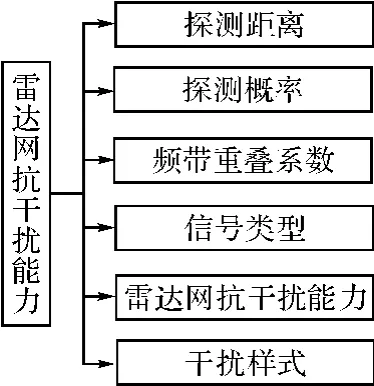
图1 雷达网抗干扰效果评估模型

雷达网的整体性能指标很多，如何选取合适的性能指标进行评估是十分关键的。为了方便讨论，从中选取了几个影响雷达网抗干扰效果较为典型的指标，建立了相应的雷达网抗干扰效果模型见图1［8］。

1）探测距离R

雷达网的探测距离是指目标被发现时到各个受保护目标的距离。该距离可由雷达网中所有单个雷达的探测距离中的最大值得到，它反映了雷达网的预警能力。

2）探测概率P

假设n部雷达中第i部雷达对第m个目标的探测概率为Pim，则雷达网对第m个目标的探测概率为

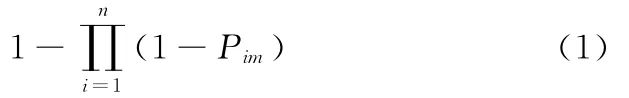
3）频带重叠系数η

在雷达数目一定的情况下，各部雷达占有的频带越宽，抗干扰性能越好，所以在衡量雷达网抗干扰效能优劣时，不但要充分考虑到各雷达的频率、带宽，更应注重雷达间的带宽重叠的状况。

4）信号类型s

雷达网中拥有的信号类型越多，则其反侦察、抗干扰能力强。

5）雷达网抗干扰能力AJ

组网的各部雷达的抗干扰能力视其在网中的地位而对雷达网的整体抗干扰能力的贡献是不同的，各雷达的作用距离作为其对整体网贡献的加权系数，最后求得整个雷达网抗干扰能力。

6）干扰样式S

干扰样式必须与雷达体制相匹配，才能获得较好的干扰效果。对于具有一定干扰措施的干扰机，如果被干扰雷达具有对应的抗干扰措施，这种干扰措施往往不成功；如果被干扰雷达没有对应的抗干扰措施，这种干扰措施就可能成功。

3 RBF神经网络

RBF神经网络是以函数局部逼近理论为基础的前向神经网络，即对于输入空间的某一个局部地区只存在少数的神经元用于决定网络的输出，具有最佳逼近的特性，且无局部极小值问题存在，较强的输入和输出映射功能，是完成影射功能的最优网络［9］。

RBF神经网络的基本思想是：用径向基函数（RBF）作为隐含的“基”，构成隐含层空间，隐含层对输入矢量进行变换，将低维的模式输入数据变换到高维空间内，使得在低维空间内线性不可分问题在高维空间内线性可分。

RBF神经网络的结构与多层前向网络相似，它是以函数局部逼近理论为基础的前向径网络，即对于输入空间的某一局部地区只存在少数的神经元用于决定网络的输出，其具有最佳逼近的特性，且无局部极小值问题存在，具有较强的输入与输出映射功能，是完成映射功能的最优网络。

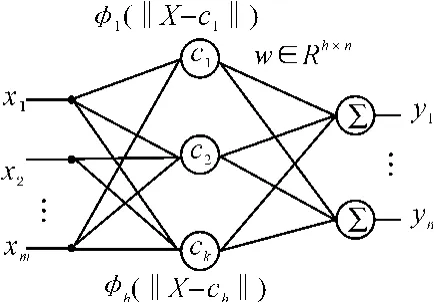
图2 RBF神经网络结构

3.1 RBF神经网络结构

RBF神经网络的结构是一种三层前馈网络，由输入层、隐含层和输出层构成，如图2所示。

RBF神经网络最显著的特点就是隐节点的基函数采用距离函数，并且使用径向基函数作为激活函数。径向基函数关于n维空间的一个中心点具有径向对称性，而且神经元的输入离该中心越远，神经元的激活程度就越低。因此每个隐节点都有一个数据中心，图2中ci就是网络中第i个隐节点的数据中心值，‖＊‖表示欧式范数。径向基函数则可以采用多种形式，一般取高斯函数：

式中，δi为该基函数的扩展常数或宽度。在图2中，RBF网络的第n个输出可以表示为

3.2 神经网络学习算法

RBF神经网络的学习算法主要解决以下问题：如何确定网络隐节点数；如何确定各径向基函数的数据中心及扩展常数；如何修正输出权值；常用的学习算法有K－means方法、梯度法和OLS算法。本文采用OLS学习算法。OLS学习算法每一次循环只产生一个神经元，而每增加一个神经元，都能最大限度地降低误差，如果未达到精度要求则继续增加神经元，直到满足精度要求或达到规定的最大神经元数目为止。该方法比较容易实现，还能在权值学习的同时确定隐节点的数目，并且保证学习误差不大于给定值。OLS的具体算法许多文献已有详细介绍，本文便不赘述，感兴趣的可详阅参考文献［13］。

4 实例仿真

图3 RBF神经网络训练图

以某雷达网为例，得到15次测量样本。对指标样本原始数据进行归一化处理如表1所示。

将表1中的前15组样本作为训练样本，对RBF神经网络进行训练。仿真参数设置为：训练精度goal＝1e－5，径向基层的扩展常数δ＝1。训练结束后，用样本16、样本17和样本18对于网络进行检验，神经网络训练如图3所示。从图3可以看出，当训练仿真到10次时（RBF的隐节点的个数为10），达到设定的训练精度。

从表1可以看出，测试样本的误差分别为－0.0013、0.0010和－0.0008这些误差基本上在可以接受的误差范围之内，因此，该网络可以用来进行雷达网抗干扰效果的评估。

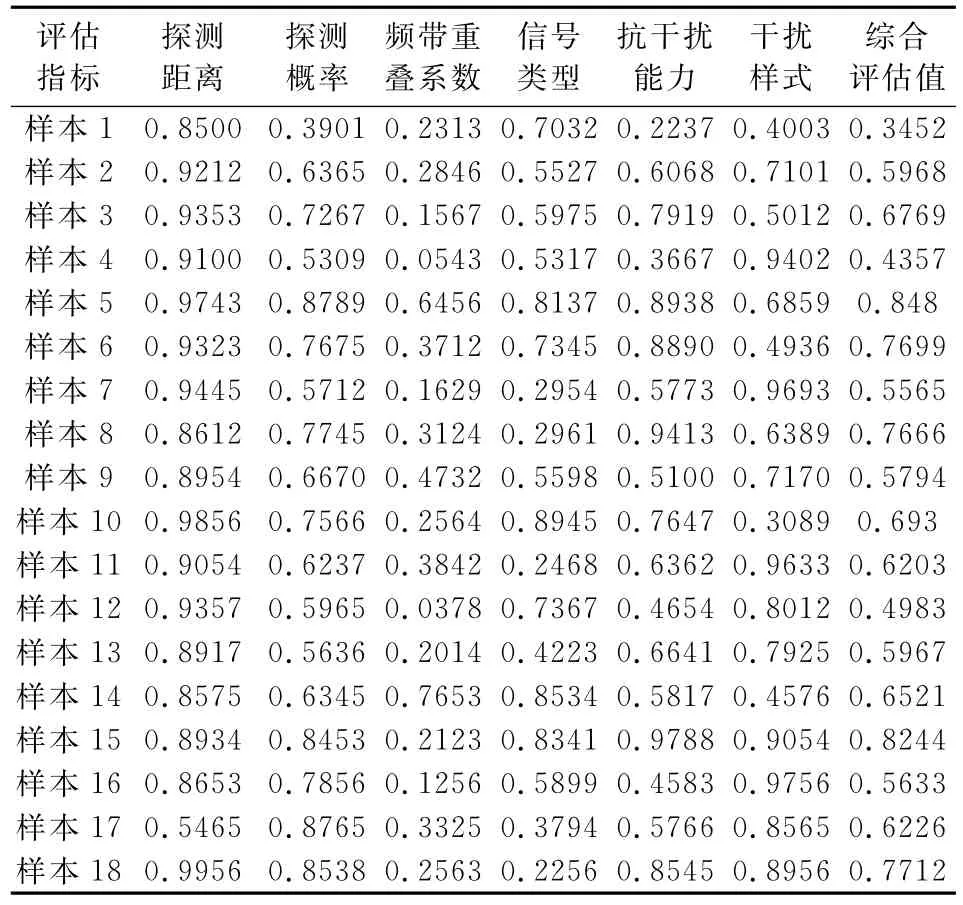
表1 归一化数据

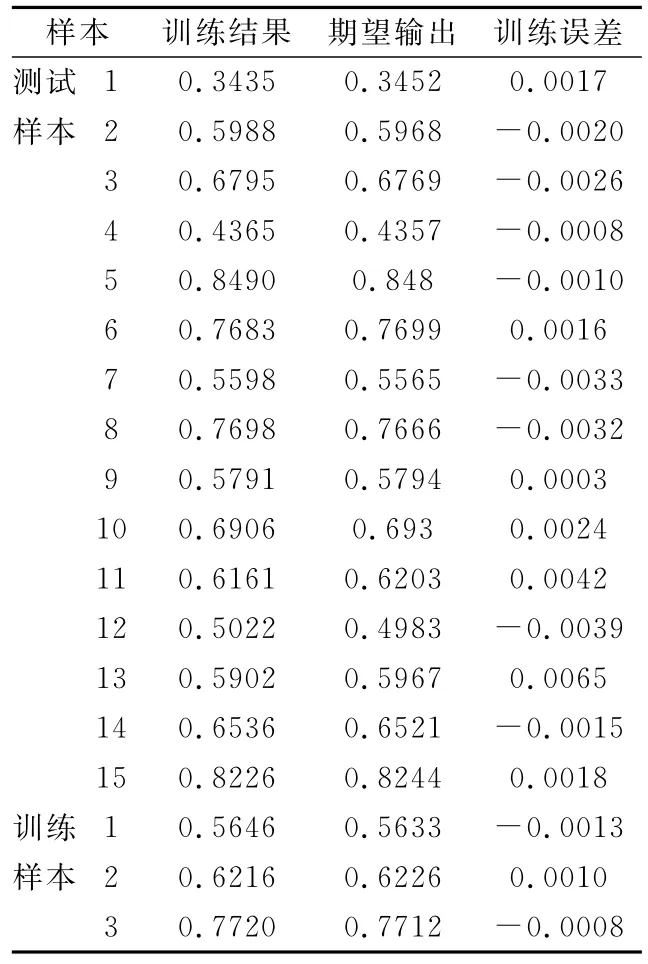
表2 训练与测试结果

5 结语

通过以上仿真分析可以看出，利用RBF神经网络对雷达网抗干扰效果进行评估具有较好的实用性和可行性，但对于RBF神经网络而言，要使得网络的输出结果更加准确，就必须使样本数据更加准确。由于雷达网抗干扰效果评估是一项非常复杂的工程项目，影响其抗干扰效果的因素有很多，因此在试验实施中，可能会因为各种原因，造成最后结果的巨大差异，所以，该评估方法对样本数据有很高的要求。此外，还需要进一步考虑如何最优化选取神经网络径向基层的扩展常数和神经元数目。

［1］王国玉.电子系统建模仿真与评估［M］.长沙：国防科技大学出版社，2000.

［2］李宗吉，王树宗.武器装备系统效能评估的几种方法［J］.海军工程大学学报，2000（1）：97－101.

［3］侯印铭，李德成，等.综合电子战［M］.北京：国防工业出版社，2000.

［4］郭齐胜，郅志刚，杨瑞平，等.装备效能评估概论［M］.北京：国防工业出版社，2005.

［5］尹永刚，黄德永，李建勋.基于神经网络的雷达抗干扰方法综述［J］.雷达与对抗，2008（1）：5－8.

［6］杨志强，何芳，谢虹.基于BP神经网络的雷达网抗干扰性能综合评估［J］.火力与指挥控制，2005（4）：41－44.

［7］孙卓光，熊家军.基于改进BP网络的雷达网抗干扰性能评估［J］.微计算信息，2009（25）：243－244.

［8］王国玉，汪连栋，王国良，等.雷达电子战系统数学仿真与评估［M］.北京：国防工业出版社，2004.

［9］白炜，鞠儒生，邱晓刚.基于RBF神经网络的作战效能评估方法［J］.系统仿真学报，2008（12）：6391－6393，6397.

［10］康珺，孟文俊.一种基于改进神经网络的系统辨识方法［J］.计算机与数字工程，2012（1）.

［11］吴珂，杨丽霞，王海瑞.量子神经网络在电力谐波检测中的应用［J］.计算机与数字工程，2012（2）.

［12］夏红霞，王惠营，胡磊.基于粗糙集的神经网络结构优化方法［J］.计算机与数字工程，2010（5）.

［13］刘金玲.基于OLS算法的RBF网设计方法与实现［J］.计算机时代，2001（7）：21－23.