基于遗传算法的反卫星拦截轨道优化

杨 亮，武 健，马 肸

(第二炮兵工程大学 603 室，西安 710025)

随着空间技术的发展，空间对抗日益增强，作战领域空间化的发展趋势不断明朗，外层空间必然成为今后的主战场。利用空间停泊武器有效杀伤敌方外层航天器无疑是削弱敌方空间力量强有力的手段。

对于空间拦截，以冲量拦截方法应用最为广泛，国内不少学者也对最优冲量拦截进行了深入研究。众多学者针对直接发射拦截、路径约束拦截、时间固定及有时间约束拦截等实际问题，利用不同的动力学方程进行研究，给出冲量解得性质和一些其他的结论［3-5］。同时优化理论在轨道拦截计算中得到广泛使用，如非线性规划法、遗传算法、蚁群算法、退火算法等［6-7］。针对单脉冲轨道机动样式，在固定时间最优能量机动的基础上建立了基于遗传算法的反卫星拦截器在轨机动拦截的优化模型。

1 坐标系和研究假设

本文只考虑椭圆轨道情况。定义赤道惯性坐标系OXYZ:坐标原点在地球中心;X 轴沿地球赤道面和黄道面的交线，指向春分点γ;Z 轴指向北极;Y 轴在赤道面上垂直于X轴。

在此做如下的假设:

1)地球为半径Re=63 711 110 km 的圆球，地球引力场为距离平方反比力场，地球引力常数μ =3.986 004 418 ×1014m3/s2。

2)对反卫星拦截器施加的推力以冲量形式作用，所以在变轨机动点时所获得的速度增益为瞬时速度增益。

3)不考虑空间中拦截器受晒、测控支持、引力和大气阻力等的摄动问题，并略去地球旋转对拦截器飞行运动的影响。

2 实时位置及速度建模

现已知拦截器及目标卫星轨道的6 个根数，即(a，e，i，Ω，ω，tP)，则描述其位置和速度步骤如下:

在惯性空间，拦截器及目标卫星某时刻位置矢量r 可以表达如下

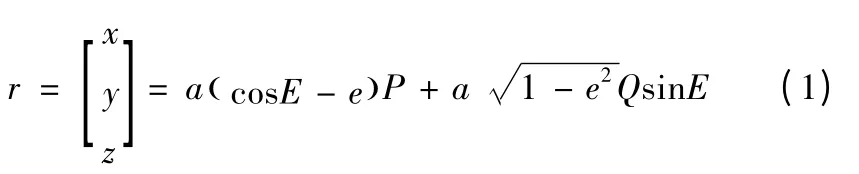
对式(1)进行微分

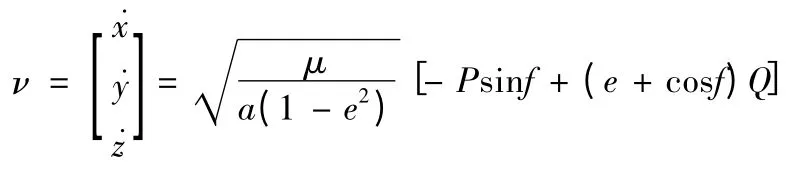
其中

利用坐标转换，单位矢量P，Q 在赤道惯性坐标系中表达如下:

在轨道根数已知下，先解开普勒方程，再代入式(1)即可得到拦截器及目标卫星的实时位置，用迭代法解开普勒方程的过程如图1 所示。

图1 迭代流程

3 轨道机动拦截模型

如图2 所示，反卫星拦截器运行初始轨道为轨道Ι，t 时刻拦截器的位置矢量和速度矢量分别为r1和v1，假定在该时刻对其施加速度冲量Δv，使拦截器的速度矢量变为ν2，并进入另一条轨道F，经Δt 秒后命中预定的空间位置矢量为vm的目标卫星。

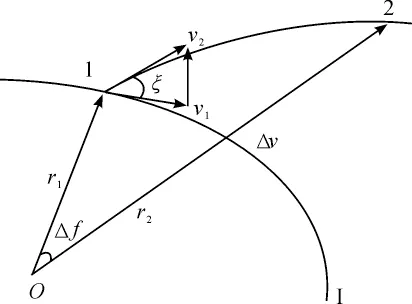
图2 轨道拦截示意图

记轨道F 的半通径为P2，偏心率为e2，则r1和r2的夹角为Δf(即真近点角之差)，计算如式(2)所示。

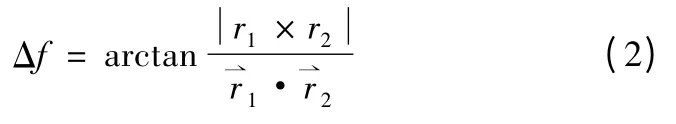
设定

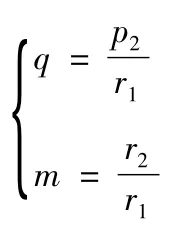
(E1，E2为解开普勒方程所得的偏近点角)

则有e2，p2关系式为

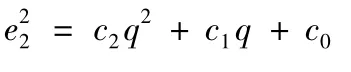
c2，c1，c0分别为

根据活力公式及动量守恒定理即可计算v2(Θ2为终极轨道的速度倾角)

则初、终轨道的夹角

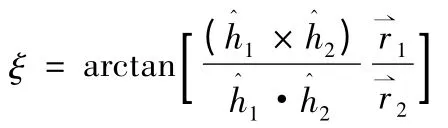
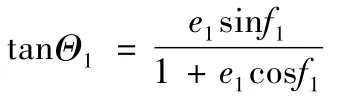
则最终可以得到轨道坐标系下的Δv

4 遗传算法思想及设计

遗传算法是一种随机的全局搜索方法，模仿自然生物进化的一些方面。其不要求优化函数具备连续、导数存在等假设，又不需要先验经验，能很快地收敛到最优解附近，因此用来解决轨道拦截优化的问题具有一定的优越性。采用遗传算法求解的主要内容包括问题解的基因表示，个体的适应度函数，以及对种群的遗传操作。

1)问题解的基因表示

将反卫星轨道机动拦截优化设计转化为对时间点的优化搜索，遗传基因表示为拦截器机动开始时刻t1和拦截时刻t2，采用十进制编码方式进行编码。为保证两个基因具有足够的选择，编码时每个基因所需要的十进制数的位数为8位，如图3 所示。

图3 基因编码图

2)适应度函数

基于单脉冲机动拦截，本文对能量进行优化，即需要能量最小，故遗传算法的适应度函数可表示为:Fitness=Δv。

3)遗传操作

选择算子。采用比例选择算子，选择适应度值较小的个体作为下一代的群体的父代。在优化问题当中，最优解可能在解空间的边界或在非可行解的附近，如果全部舍去非可行解则可能减少获得最优解的概率，因此在算法中以较小的概率选择非可行解，与可行解一起进行交叉、变异操作。交叉算子。采用单点交叉方式，随机挑选种群中两个个体作为交叉对象，并随机产生一个交叉点位置。变异算子。随机选择群体中的个体并随机产生变异点位置。

4)遗传算法参数的选择

遗传算法的参数包括种群数目、遗传的代数、交叉和变异的概率。参数的选择是一个开放的问题，目前还没有一个统一的选取规则，尤其是各个参数之间的相互影响更是难以精确的表达.这里选择根据经验和多次实验，设定如下的参数:种群数目为50，遗传代数为100，交叉概率为0.8，变异概率为0.1。

5 仿真算例

在此假定已经通过地面测量设备得到反卫星拦截器及目标卫星轨道的6 个根数，如表1 所示。

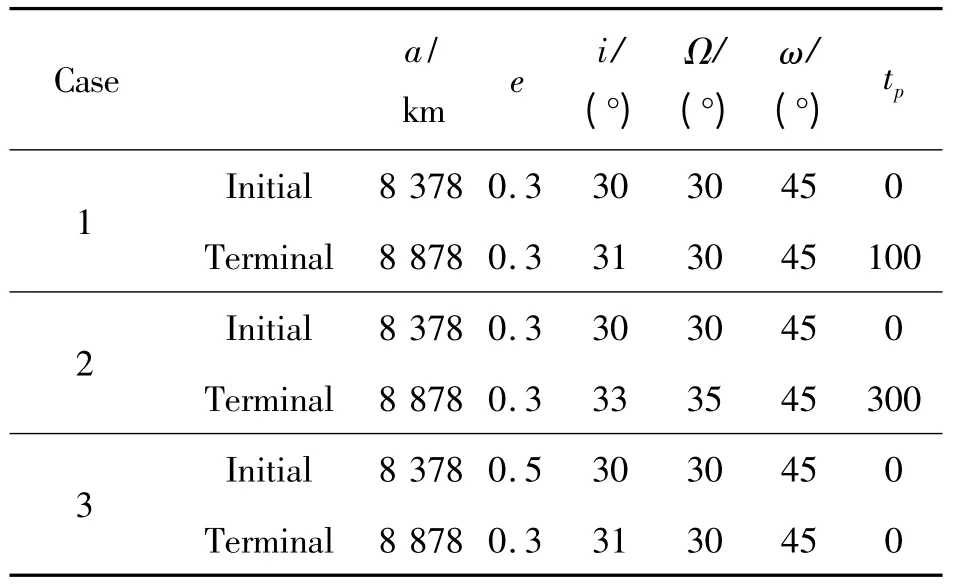
表1 最优能量问题仿真条件表

经仿真计算得到最优能量迭代变化如图4 所示。

从结果看出，应用遗传算法搜索，迭代不需要太多次数，即能够得到一个满足约束条件可行的最优解。

图4 迭代图

将优化设计结果值代入卫星工具包(STK)进行检验，得到的末端位置误差如表2 中Δr/m 一栏所示，结果表明了迭代算法的正确性。

表2 速度增量、飞行时间及末端误差

从结果看出，应用遗传算法搜索，迭代不需要太多次数，即能够得到一个满足约束条件可行的最优解。

6 结束语

本文从空间作战的角度出发，为优化在轨拦截器对某一目标卫星的拦截轨道，提出了基于遗传算法优化反卫星拦截器机动拦截的模型，并以算例进行全轨道最小能量优化仿真计算。结果表明，应用遗传算法可行有效且搜索速度较快，所得优化结果满足各约束条件。

［1］任萱.人造地球卫星轨道力学［M］.长沙:国防科技大学出版社，1988.

［2］云庆夏.进化算法［M］.北京:冶金工业出版社，2000.

［3］白洪波，马书兴，朱丽萍，等.空间作战中固定时间轨道拦截的仿真研究［J］.航天控制，2006，24(4):62-65.

［4］徐晓静，张恒源，李智.空间作战中的轨道拦截建模与仿真［J］.装备指挥技术学院学报，2005，16(5):60-63.

［5］马丹山，王明海，鲜勇，等.逆轨道拦截卫星轨道设计与优化［J］.飞行力学，2009(10).

［6］王石，祝开建，戴金海.用进化算法求解轨道转移的时间——能量优化问题［J］. 宇航学报，2002，23(1):73-75.

［7］齐映红，曹喜滨.基于遗传算法的最优多脉冲交会轨道设计［J］.哈尔滨工业大学学报，2008(9).

［8］YOUNG H K，DAVID B S.Optimal Spacecraft Rendezvous Using Genetic Algorithms［J］.Journal of Space—craft and Rockets，2002，39(6):859-865.