有噪复杂度寻踪的不动点算法

陈寿齐，周伟科，焦长君，何庆国

(中国人民解放军73911 部队，南京 210002)

盲源分离(BSS)是1 种用于数据分析的信号处理方法，他是在系统输入源信号未知(或部分未知)、系统传输特性也未知的条件下，利用一些预知特性，如源信号间相互独立、源信号间的相关系数为零、某1 路源信号在特定的时延具有很强的自相关性等先验特性，从接受到的混合信号分离出所想要得到的各个源输入信号［1］。众多研究表明，盲源分离在语音信号处理、图像信号处理、生物医学信号、无线通信系统等［2］许多领域得到了广泛的应用。

独立成分分析(ICA)是基于输入源信号间具有相互独立性的1 种分析方法。然而，在许多实际应用中，混合的往往不是相互独立的随机变量，而是时间信号或者时间序列。标准的ICA 忽视了信号的时序结构，仅用信号的非高斯性即相互独立性作为分离信号的判据，这就使得该方法的使用具有一定的局限性，特别是在某些条件下，假如输入源信号具有时序特性，也可使用这些信号的时序特性估计源信号成分。

1 个由Hyvärinen 提出的、有理论基础的，利用信号的非高斯性和时间相关性这2 个特性的信号分析方法就是复杂度寻踪［3］。复杂度寻踪是投影寻踪向时间序列数据即具有时序结构信号的扩展，目的是发现具有感兴趣结构的时间序列的投影。对于复杂度寻踪，Hyvärinen 采用梯度下降的优化算法，来从时间序列中分离感兴趣的成分。但由于梯度下降算法具有一定缺点，如收敛速度慢、需要对不同的问题选择合适的学习步长，使得算法的应用受到了一定的限制。

针对上述算法的不足，Shi 等［4］提出了复杂度寻踪的不动点算法，该算法计算简单，不需要用户选择学习步长，并且算法有快速稳定收敛的性质。

上述2 种复杂度寻踪算法是在不考虑噪声，或者噪声影响可忽略的情况下推导的。但是，在实际应用中，噪声的影响是不可避免的。因此，在设计算法时候，必须要考虑到噪声的影响。

近年来，许多学者对有噪情况下的盲源分离算法进行了研究。Hyvärinen 等［5］提出了基于高斯矩的有噪独立成分分析的不动点算法，该算法考虑了当源信号相互统计独立时，噪声对算法性能的影响，相比于FastICA 算法［6］，该算法具有更好的信号分离性能。Shi 等［7］提出了基于高斯矩的有噪的复杂度寻踪算法，该算法考虑了源信号具有时序结构特性时，噪声对算法性能的影响，相对于不考虑噪声影响的复杂度寻踪算法，该算法具有更好的信号分离性能，但是该算法采用了梯度下降算法的优化方法，存在收敛速度慢，需要选择学习步长等问题，使得该算法的实际应用受到一定的限制。

综合上述几种算法的优缺点，针对有噪背景下，具有时序结构特性信号的盲分离，本文提出了有噪复杂度寻踪的不动点算法。

1 提出算法

1.1 准白化

假设观测信号x(t)= [x1(t)，…，xm(t)]T用矩阵方程描述为

其中:A 是 m × m 维 的 未 知 混 合 矩 阵;s (t) =s1(t)，…，sm([t])T是未知的具有时序结构特性的源信号矢量，假设该信号具有零均值和单位方差;n (t)=n1(t)，…，nm([t])T是加性高斯白噪声。高斯噪声n(t)和源信号s(t)相互统计独立。高斯白噪声n(t)的协方差矩阵定义为

在噪声存在的情况下，对观测信号x(t)的白化预处理就必须要考虑到噪声的影响，如果噪声的方差已知或者可以估计，这样的方法是简单的。观测信号x(t)的协方差矩阵为:正常的无噪声存在情况下的白化方法就要变成为下面的准白化，也就是准白化的数据~x(t)满足有噪的独立成分分析的模型

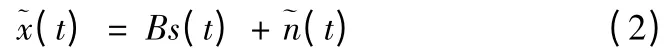
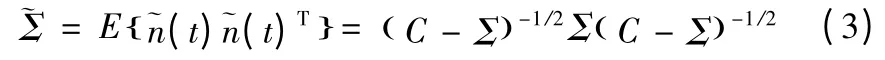
1.2 目标函数

对于无噪声情况下的数据模型:y(t)=Bs(t)，考虑信号z(t)=wTy(t)的预测编码，w 表示1 个使得z(t)=wTy(t)的非高斯性极大化的方向，z(t)的值是由前面的值通过某些函数来预测的

其中:T 为信号的样点数;δz 定义为具有冗余边际分布的随机变量，假设信号是平稳的。为了在实际中使用式(5)的逼近，需要固定预测函数f 的结构并且找到δz 熵的逼近。使用计算简单的线性自回归模型作为预测结构

假设知道冗余概率密度对数的1 个很好的逼近，记为G(·) ，可以获得如下的1 个逼近

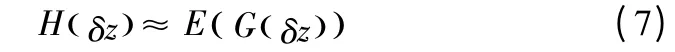
为了发现最感兴趣的方向w，利用z(t)=wTy(t)并结合如上所述的复杂性逼近。可以用1 个仅带w 的目标函数来表示复杂性逼近

上述的目标函数即式(8)没有考虑噪声的影响，如果可以从有噪的观测信号中估计出上述的无噪的数据那么上述的目标函数即式(8)就可以用到有噪的复杂度寻踪中去，关键是如何选择合适的函数G(·) ，使得可从有噪的观测数据中估计出

定义协方差为c2的高斯密度函数

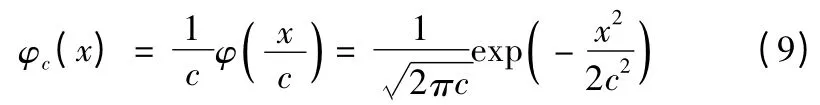
那么有下面的定理［5，8］。

定理1 对于任意的非高斯随机变量v，n 表示方差为σ2的高斯噪声变量，定义高斯函数φ 如式(9)，那么对于任意的c ＞σ2有下面的表达式成立

此定理说明可通过最小化目标函数即式(8)来从有噪的观测数据中估计出独立成分。这里通过选取G(u) =使得可估计出无噪的数据这个期望形式的表达式叫做高斯矩，那么由式(8)和式(10)就能通过最小化公式(11)估计出有噪的ICA 模型。

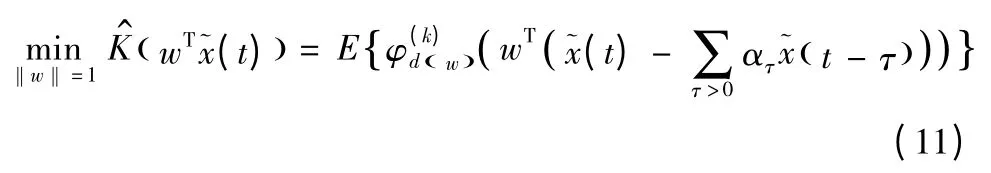
1.3 学习算法

在推导学习算法之前，定义如下的表达式:

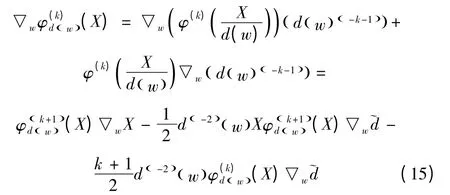
利用文献［8］中的引理

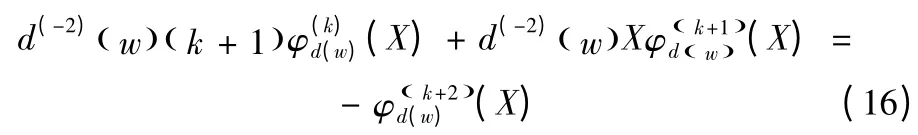
这意味着式(15)可表示为如下形式

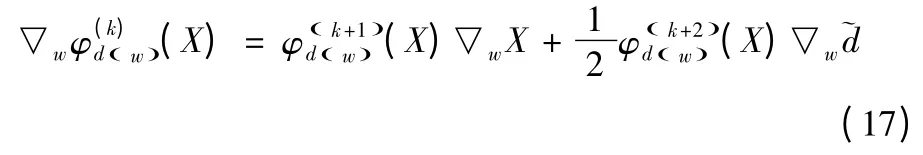
有噪的复杂度寻踪的不动点算法为

结合式(19)和式(20)，得到有噪复杂度寻踪的不动点算法如下

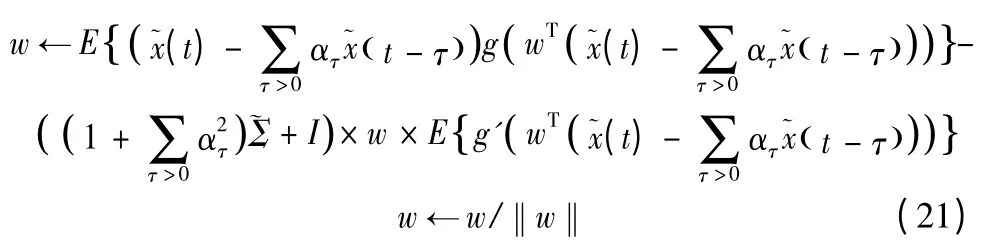
其中的g(·) 是函数G(·)的一阶导函数，可选择为g(u)=tan h(u)，g'(·) 是函数g(·) 的一阶导函数。

算法的简单特例是自回归模型为一阶的情况

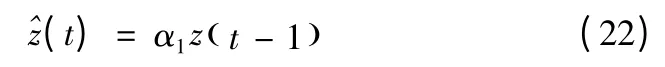
延迟不需要为1，但这是个标准的例子。算法中的参数α1可用最小二乘法来估计

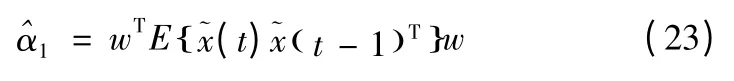
综上所述，可以获得有噪复杂度寻踪的不动点算法如下:

1)中心化观测信号x(t)，使得其均值为零;

3)随机选择单位范数向量w 作为迭代的初始点;

4)估计自回归系数ατ，对于一阶自回归模型，作=

5)作不动点迭代:

其中的g(·)函数选择为g(u)=tanh(u);

6)如果不满足终止条件，返回步骤4。

算法终止条件为:迭代前的w 和迭代后的w 同指1 个方向，也就是其内积等于或接近于1。可使用收缩策略或对称正交化的过程来估计分离矩阵

1.4 与其他算法的关系

假设信号没有时间结构，这就意味着信息过程等于信号本身，这样有噪复杂度寻踪的不动点算法就可简化为:

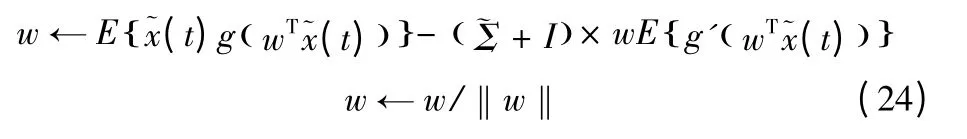
这个算法就是在实际应用中所广泛采用的文献［5］中算法。

如果没有背景噪声的影响，这样有噪复杂度寻踪的不动点算法可以简化为:

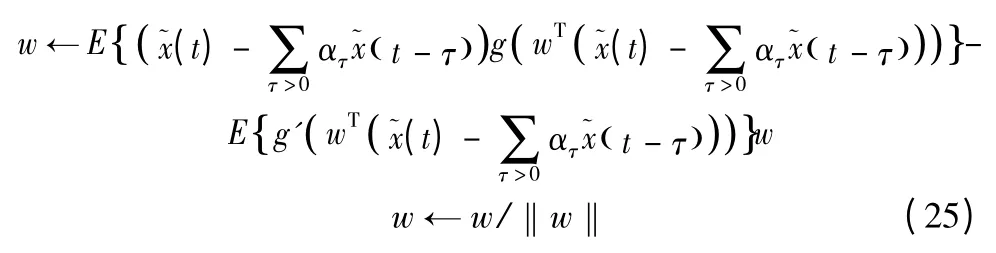
这个算法就是文献［4］中的算法。

在没有背景噪声和假设信号没有时间结构特性的情况下，有噪复杂度寻踪的不动点算法还可以进一步简化为:

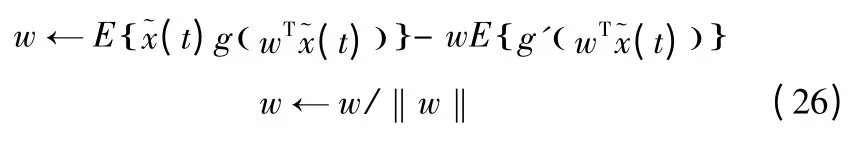
这个算法就是在实际应用中所广泛采用的FastICA 算法［6］。

2 计算机仿真

为验证本文提出算法的有效性和具有较好的信号分离性能，采用人工信号和自然图像对本文提出算法进行分离仿真。采用PI 性能指数来评价算法的分离性能，具体的定义如下

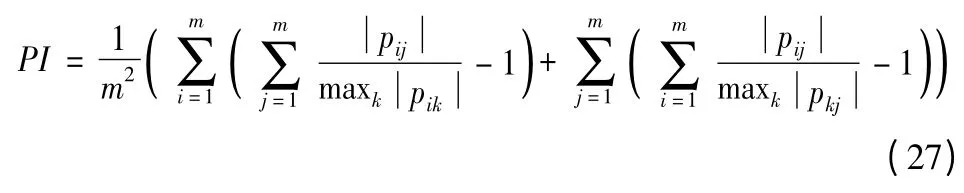
其中:pij是m×m 维全局矩阵P =WVA 的第i 行和第j 列的元素。PI 值越小，算法的分离性能越好。

2.1 人工信号的分离

生成6 路AR(1)模型信号来用于仿真。信号1，2，3 和4是由超高斯更新生成的，信号5 和6 是由高斯更新生成的;所有的信号都具有单位方差。信号1，3 和5 具有相同的自回归系数(0.25)，因此有相同的自协方差;信号2，4 和6 具有相同的自回归系数(0.5)，信号的样点数为5 000，生成的6 路人工信号如图1 所示。

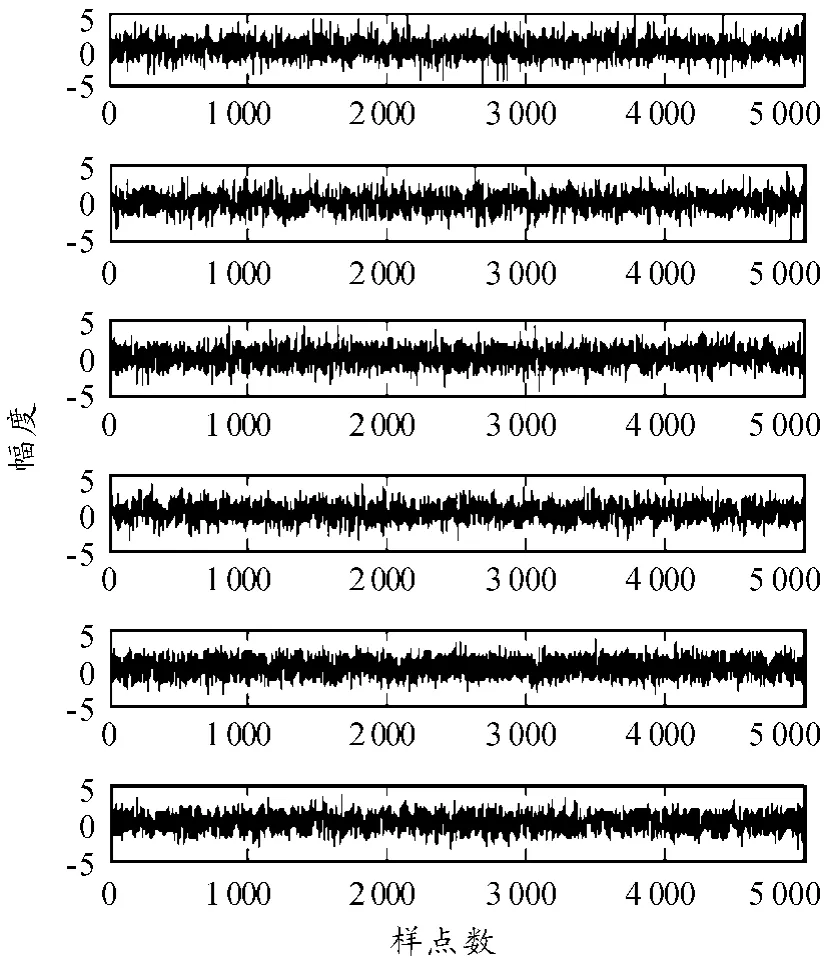
图1 源信号

这6 路信号用Matlab 随机产生的6 ×6 维矩阵进行混和，加性高斯白噪声的方差为0.01I。采用文献［4］算法(记为FPCP 算法)、文献［5］算法(记为FastNoisyICA 算法)、文献［7］算法(记为NoisyCP 算法)和本文提出的算法对这6 路信号进行分离。相应的仿真参数设置为:FPCP 算法、Noisy-CP 算法和本文提出的算法都采用一阶自回归模型;4 种算法中的(g)· 函数都选择为非线性函数g(u)= tan h(u);NoisyCP 算法采用了梯度下降的优化方法，学习步长选择为1，其他3 种算法都是不动点算法，不需要选择学习步长;4 种算法的分离矩阵都采用对称正交化的方法进行处理。

为了评价上述4 种算法分离信号的性能，采用式(27)的性能指数定义。4 种算法迭代到固定迭代次数N 时停止，迭代次数N 由0 变化到200。对于每1 个固定的迭代次数N，算法独立运算200 次，每次信号都用随机生成的矩阵来混合，并计算每次的性能指数，最后的性能指数是这200 次的平均性能指数，结果如图2 所示。

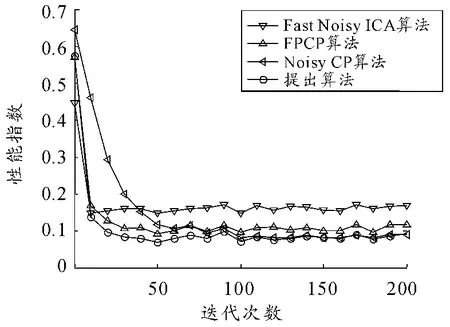
图2 性能指数曲线

FastNoisyICA 算法迭代收敛后的平均性能指数为0.167 8，FPCP 算法的平均性能指数为0.116 5，NoisyCP 算法的平均性能指数为0.090 1 和本文提出的算法的平均性能指数为0.085 6。由上述的PI 性能指数的定义可知，PI 值越小，分离效果越好。也就是说，4 种算法中，本文提出的算法和NoisyCP 算法对6 路混合信号的分离效果最好，FPCP 算法的分离效果次之，FastNoisyICA 算法的分离效果最差。

图3给出了4 种算法在稳定状态下的平均性能指数曲线.4 种算法仿真的信噪比范围为-20 ～40dB，算法最大迭代次数为200 次，每种算法独立运行200 次，每次信号都用随机生成的矩阵来混合，并计算每1次的性能指数，最后的性能指数是这200 次的平均性能指数。可以看出:这4 种算法中，FastNoisyICA 算法的分离效果最差，FPCP 算法的分离效果次之，NoisyCP 算法和本文提出的算法的性能相当;对于FPCP 算法、NoisyCP 算法和本文提出的算法在信噪比大于30 dB 时的性能指数趋于一致，也就是，在高信噪比条件下，噪声对算法的影响比较小。

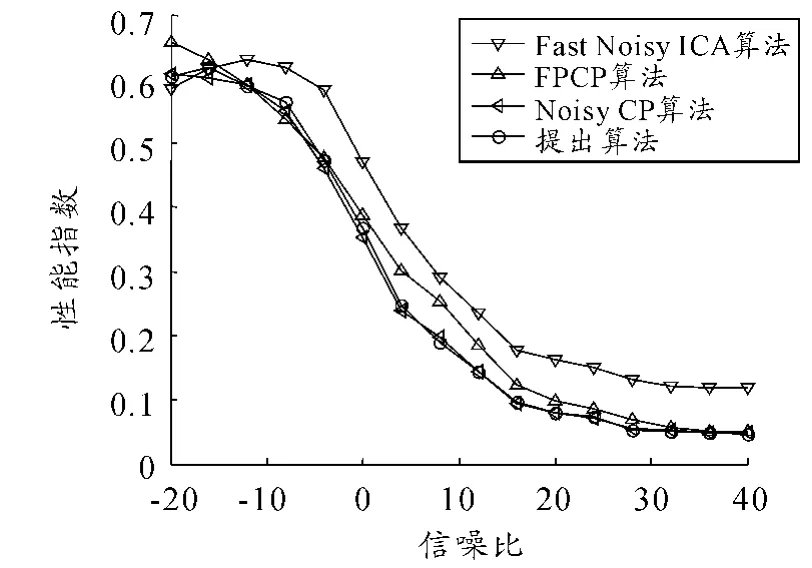
图3 稳定状态下的性能指数曲线

表1 给出了在4 种算法独立仿真500 次，最大迭代次数为200 次时，每种算法达到收敛时平均消耗的CPU 时间(主频为2.4GHz Core(TM)2 Duo 处理器的PC 机)。

表1 4 种算法消耗的CPU 时间 s

由表1 可以看出，4 种算法消耗的时间由少到多依次为:FPCP 算法、本文提出的算法、FastNoisyICA 算法和NoisyCP算法。这是因为:FastNoisyICA 算法、FPCP 算法和本文提出的算法都为不动点算法，收敛速度相对快于采用梯度算法的NoisyCP 算法。NoisyCP 算法和本文提出的算法，在对信号的分离性能方面效果一致，但是本文提出的算法消耗的时间要明显少于NoisyCP 算法。

通过以上对人工信号的仿真可以看出，本文提出的算法相比其他3 种算法，在信号的分离性能和收敛速度这2 个方面都具有很大的优势。

2.2 自然图像的分离

用图4 第1 行所示的4 幅自然图像(128 ×128)来进行仿真试验，相应的归一化峭度值从左到右依次为:-0.611 5、-0.432 5、1.760 0 和23.931 4。

计算这4 幅自然图像的协方差矩阵得

由上述协方差矩阵知这4 幅自然图像不是相互统计独立的，他们之间具有一定的相关性。用Matlab 随机产生的4×4 维的矩阵对这4 幅图像进行混合，加性高斯白噪声的方差为0.01I，得到4 幅混合后的图像。对混合后的图像分别采用FPCP 算法、FastNoisyICA 算法、NoisyCP 算法和本文提出的算法进行分离试验。相应的仿真参数设置为:FPCP 算法、NoisyCP 算法和本文提出的算法都采用一阶自回归模型;FPCP 算法、FastNoisyICA 算法、NoisyCP 算法和本文提出的算法中的非线性函数g(u)都选择为g(u)=tan h(u);NoisyCP算法的学习步长选择为1，其他3 种算法都是不动点算法，不需要选择学习步长;4 种算法都采用对称正交化的方法来处理分离矩阵。

4 种算法的分离结果如图4 所示，可以看出，FPCP 算法分离出来的第4 幅图像中明显的含有其他干扰图像，Fast-NoisyICA 算法分离出来的第4 幅图像中明显含有其他干扰图像，只有NoisyCP 算法和本文提出的算法成功实现了对4幅图像的分离。

为了验证这4 种算法分离图像的效果，采用式(24)定义的性能指数，算法迭代到固定迭代次数N 时停止，迭代次数N 由1 变化到200。对于每个固定的迭代次数N，算法独立运算200 次，每次图像都用随机生成的矩阵来混合，并计算每次的性能指数，最后的性能指数是这200 次的平均性能指数，结果如图5 所示。

图4 自然图像的盲分离

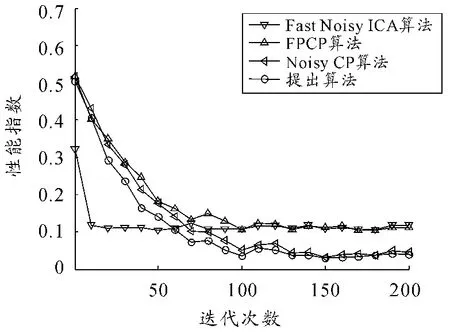
图5 性能指数曲线

4 种算法收敛后的平均性能指数为:FPCP 算法为0.212 4、FastNoisyICA 算法为0.218 7、NoisyCP 算法为0.146 9 和本文提出的算法为0.140 9。因为性能指数越小，信号的分离效果越好。在信号的分离效果方面:NoisyCP 算法和本文提出的算法的分离效果要好于FPCP 算法和FastNoisyICA算法。

图6给出了4 种算法在稳定状态下的平均性能指数曲线，4 种算法仿真的信噪比范围为-20 ～40 dB，算法的最大迭代次数为200 次，每种算法独立运行200 次，每次信号都用随机生成的矩阵来混合，并计算每次的性能指数，最后的性能指数是这200 次的平均性能指数。可以看出:这4 种算法中，在信噪比大于20 dB 时，FastNoisyICA 算法的分离效果最差，FPCP 算法的分离效果次之，NoisyCP 算法和本文提出的算法的性能相当，对于FPCP 算法、NoisyCP 算法和本文提出的算法在信噪比大于36 dB 时的性能指数趋于一致，也就是说，在高信噪比条件下，噪声的影响可以忽略不计。

图6 稳定状态下的性能指数曲线

表2 给出了在2 种算法独立仿真500 次，最大迭代次数为200 次时，每种算法达到收敛时平均消耗的CPU 时间(主频为2.4GHz Core(TM)2 Duo 处理器的PC 机)。

表2 4 种算法消耗的CPU 时间 s

由表2 可以看出，4 种算法消耗的时间由少到多依次为:FastNoisyICA 算法、FPCP 算法、本文提出的算法和NoisyCP算法。这是因为，FastNoisyICA 算法、FPCP 算法和本文提出的算法都为不动点算法，收敛速度相对要快于采用梯度算法的NoisyCP 算法。NoisyCP 算法和本文提出的算法，在对信号的分离性能方面效果一致，但是本文提出的算法消耗的时间要明显少于NoisyCP 算法。

通过对人工信号和自然图像的分离试验表明了本文提出算法的有效性，且提出算法在信号的分离性能方面要好于不考虑噪声影响的FPCP 算法和考虑噪声影响的FastNoisyICA 算法。对于与取得同样信号分离效果的NoisyCP 算法相比，本文提出的算法的用时明显要少，而且，本文算法为不动点算法，具有收敛速度快，计算简单，不需要选择学习步长等优点，因此更具有实际应用意义。

3 结束语

本文给出了当源信号具有时序结构特性时的有噪复杂度寻踪的不动点算法。计算机仿真表明了提出算法的有效性和好的信号分离性能。有趣的是，本文提出的算法还和现有算法具有一定的关系:当源信号具有时序结构特性且没有高斯噪声影响时，该算法就退化为FPCP 算法;当源信号没有时序结构特性，且有高斯白噪声影响时，该算法就退化为FastNoisyICA 算法;当源信号没有时序结构特性且没有高斯白噪声影响时，该算法就退化为FastICA 算法。

［1］Cichocki A，Amari S.Adaptive Blind Signal and Image Processing［M］.England:John Wiley ＆ Sons Ltd，2002.

［2］Barros A K，Cichocki A.Extraction of specific signals with temporal structure［J］.Neural Comput，2001，13 (9): 1995-2003.

［3］Hyvärinen A. Complexity pursuit: separating interesting components from time-series ［J］. Neural Computation，2001，13(4):883-898.

［4］Shi Z，Tang H，Tang Y. A fast fixed-point algorithm for complexity pursuit［J］. Neurocomputing，2005( 64): 529-536.

［5］Hyvärinen A.Gaussian moments for noisy independent component analysis ［J］. IEEE Signal Process Lett，1999，10(3):626-634.

［6］Hyvärinen A. Fast and robust fixed-pointed algorithms for independent component analysis［J］. IEEE Trans. Neural Networks，1999，6(6):145-147.

［7］Shi Z，Zhang C.Gaussian moments for noisy complexity pursuit［J］.Neurocomput，2006(69):917-921.

［8］Hyvärinen A. FastICA for noisy data using Gaussian moments［C］//Proceeding of the International Symposium on Circuits and Systems，1999:57-61.

［9］张西宁，廖与禾，温广瑞.一种新的盲声源分离方法及应用［J］.四川兵工学报，2010(1):136-139.