弹炮耦合问题在重力场下动力学数值仿真

林秉奇，顾克秋，周 成

(南京理工大学 机械工程学院，南京 210094)

弹丸起始扰动是影响火炮系统射弹散布的重要根源之一。它的形成和发展是由于弹丸自膛内开始运动至后效期末这一发射过程中火炮系统发射状态变化而引起的［1］。由于弹丸的前后定心部与身管阳线之间存在一定的运动间隙，在弹丸的推进的过程中，定心部与身管的阳线壁会不时地产生接触碰撞，导致弹丸的运动姿势的不断扰动变换［2］。而弹丸在这种膛内高速运动下的重力和惯性力会激励身管的扰动［3］，继而又影响到弹丸的运动。这种弹炮耦合的效应在研究弹丸飞行姿态时是不可忽略的。

目前利用有限元方法来研究弹炮耦合问题的文献并不多，文献［6］将不带膛线的身管与弹丸接触耦合，定义弹带节点的约束方程强迫弹丸沿身管轴线转动，建立了简化的弹炮耦合模型。文献［2］考虑了身管带膛线的因素对弹丸运动姿态的影响，但在整体建模方法上值得进一步研究。同时，现有的文献均未述及如何模拟重力静态平衡条件下弹炮耦合的发射过程，即在模拟火炮发射过程之前如何让模型在重力状态下达到静态平衡。此外，后坐过程中后坐阻力对身管扰动的影响以及火炮发射前身管由于自重产生的初始挠度的影响等［4，5］问题在仿真过程中都值得考虑。

基于接触/碰撞有限元方法，借助Abaqus 有限元平台，充分利用显式与隐式有限元求解器各自的优势来模拟重力平衡状态下的弹丸发射过程，研究重力场在不同求解器间的稳定传递问题，同时考虑弹丸膛内运动时后坐体的后坐过程。

1 接触/碰撞界面算法

有限元的非线性包括材料非线性，边界非线性与几何非线性3 个部分。由于两个或多个物体接触过程伴随着边界条件的变化，实际上就是边界非线性问题［7］。从本质上讲，接触问题还是带约束条件的优化问题，其中接触条件就是由一系列界面不连续的约束方程组成。假定有两个物体A 和B 在t1时刻占据空间VA和VB(图1 虚线)，当时间变为t2时，系统的构形发生了改变，两个物体发生了接触(图1 实线)。则接触界面条件可归纳［8］:

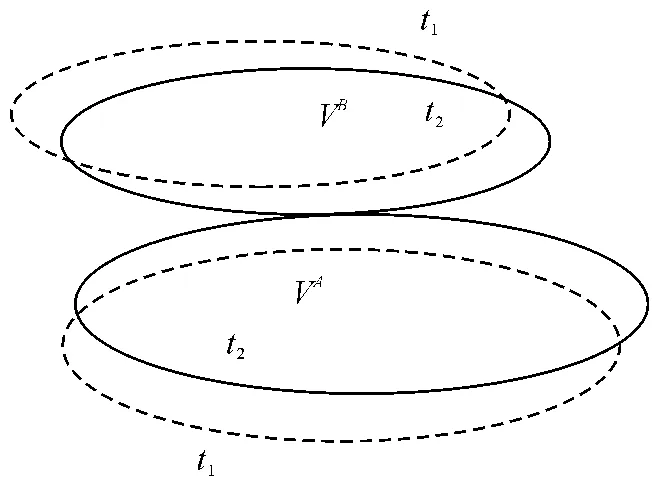
图1 接触过程中两运动物体的构型

1)无贯入条件

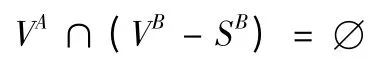
2)两物体间存在共同边界条件

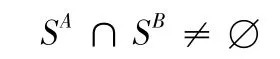
3)在边界上存在接触力

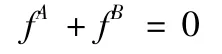
4)法向接触力不能处于拉伸状态

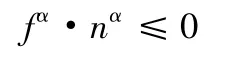
其中α=A，B

5)若接触摩擦力采用库伦摩擦模型

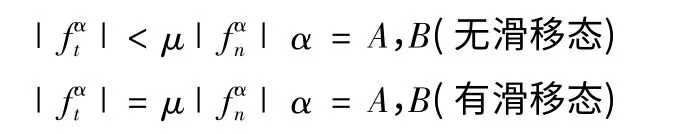
其中SA和SB分别指A 物体和B 物体的表面积，fA和fB分别指A 物体和B 物体边界上的接触力。

而将上述的接触界面约束方程引入动力学控制方程的方法较多，Abaqus/explicit 中提供了两种方法:拉格朗日乘子法与罚函数法。采用拉格朗日乘子法时，若节点配置不合理，会产生锁定，应力场不光滑等现象。且拉格朗日乘子与质量无关，故不能用于显式动力学碰撞的分析。对于表面与表面的接触，Abaqus/explicit 默认地使用动力学接触公式，其本质是利用修改加速度的值以获得正确的、增强接触约束的构形。而在一般的显式接触问题中，Abaqus/exlicit 应用罚函数接触方法来强化接触约束，用罚函数法处理接触问题，就是要求解下述泛函极值问题［9］，即

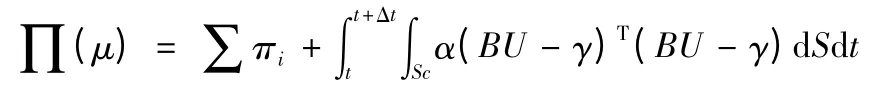
其中B 为接触约束矩阵，U 为节点位移向量，πi为第i 个物体的总势能，Sc 为接触面边界，α 为罚因子，γ 与初始法向间隙有关。采用虚功原理并做有限元离散后，得到动态接触问题的控制方程［9］

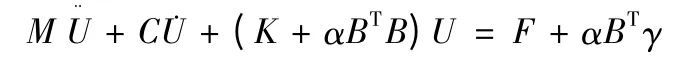
其中的位移向量U 和接触力向量F 是未知量。运用Abaqus显式算法来求解上述动力学控制方程。

2 显式隐式混合计算方法

2.1 模拟火炮发射状态时显式算法的优点

显式算法在某些特定场合下较隐式算法具备一定的优势，如计算瞬态载荷响应的高速动力学事件，利用隐式算法分析收敛时间长，甚至不易收敛。而显式算法由于利用显式前推来求解模型，所以不需要迭代与收敛准则。如果事件持续的时间非常短，显式可以得到高效率的解答。弹丸发射过程时间短，载荷瞬态加载，冲击响应剧烈，使用显式算法具备一定的优势。又如分析包括许多独立物体相互作用的复杂接触问题比隐式容易得多。弹丸发射时弹丸与身管的接触区域复杂不确定，接触碰撞剧烈，选用显式算法大大增强了其可操作性。此外，显式算法还具有与弹带材料特性相应的损伤与失效等一系列模块。

2.2 火炮初始自重静态平衡利用隐式算法的优点

火炮发射符合高速动力学的情况，且各部件接触状态复杂，利用隐式求解计算较为不易。但仅利用Abaqus 显式进行火炮发射动力学有限元仿真同样存在许多不足之处，隐式较好地补偿了显式带来的上述不足:首先，火炮发射前的静态重力平衡状态利用隐式方法计算简便，避免了显式利用准静态分析平衡过渡时的低效工作。其次，由于摇架前后套箍的间隙存在，初始装配将使得身管悬空于摇架套箍，而隐式能够在弹丸发射的初始阶段让身管外壁与摇架前后支撑点较好地接触上，排除显式计算时这种初始误差对仿真结果的干扰。最后，由于弹丸定心部的间隙存在，隐式计算能够较好地贴合弹丸发射时的初始状态，即重力状态下弹轴与身管轴线将会有一定的角度偏差。

因此，本文综合利用隐式和显式两种求解器各自的优势，将模型处理成两阶段:第一阶段，利用隐式求解得到模型重力状态下的静态平衡，第二阶段用显式延续重力状态下的弹丸发射过程。两求解器之间利用数据传递来传送位移/应变/应力场，重力场，反后坐力学特性函数(即用户子程序)，连接器的位移与连接器力等。

3 膛线身管建模与自重应力应变传递

3.1 带膛线的身管有限元模型

带膛线的身管划分网格的难度主要体现在膛线为空间曲线，要生成的空间曲面精度较差，直接划分网格带来一定的难度。文献［2］中给出了利用分段扫描映射六面体网格的较好的方法，此处不再赘述。在HYPERMESH 中通过扫描映射与参数化结构修整工具后的有限元模型如图2 所示。

图2 膛线身管有限元模型

3.2 身管自重应力应变传递

身管自重产生的挠度对弹丸的飞行姿态有一定的影响。对此建模方法，文献［11］中利用简化数值计算得到的理论挠度在HYPERMESH 的Morphing 工具中将身管有限元模型直接变形来等效身管成受重力场的状态。但在技术手段上做变形并不十分方便，而且该导入的模型并没有自重弯曲后身管的应力状态，不符合实际的自重情况。本文利用Abaqus 隐式计算获得自重状态下身管的结果导入显式中进一步计算，可以保留身管自重后的弯曲应力状态，做法也较为方便。

4 带摇架的弹炮耦合有限元模型

以后坐体(身管，炮口制退器，炮尾)，弹丸为研究对象。考虑摇架对身管的刚性支撑，固定摇架。模型所受力情况为身管与弹丸的重力，膛底压力，弹底压力，后坐阻力等，其中后座阻力通过反后坐力学特性函数(用户子程序)来实时反馈。

本有限元模型如图3 所示，采用带有沙漏控制的等参六面体缩减积分单元，共有131 723 个单元，190 050 个节点。考虑到显式隐式混合运算中传递的问题以及接触对算法的初始接触厚度问题，弹丸、身管与摇架衬套之间的接触均采用平衡主-从接触算法与罚函数法。

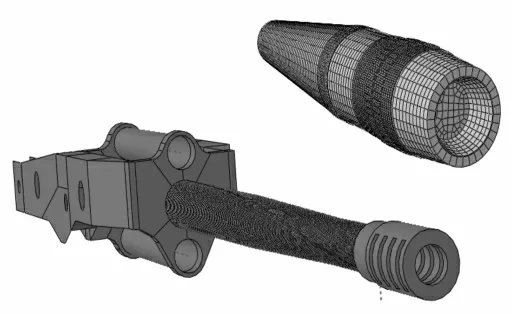
图3 带摇架的弹炮耦合有限元模型

5 动力学分析与结果

本文对于某大口径牵引火炮在发射过程中的带摇架的弹炮耦合模型进行了动力学有限元仿真，计算条件为:方向射角0 度，高低射角0 度，底凹弹，高温，全装药。前后定心部间隙为0.1 mm，不考虑弹丸质偏。定义以下坐标系为全局坐标系:沿出炮口方向为X 轴正向，Y 轴竖直向上，Z 轴根据前两轴确定。带摇架的弹炮耦合模型的仿真结果如图4至图11 所示。

弹丸的旋转过程如图7 所示，弹带部分与膛线侧壁发生的弹性接触使得弹丸在旋转运动过程中存在一定的扰动。图8 中的弹带中心位移反映了弹炮耦合效应对弹丸运动的影响，即弹丸发射时激励身管产生动态的扰动变形，这种扰动变形反过来会影响弹丸的主运动。由图8 弹丸各部分的位移值可以看出，由于前后定心部间隙存在，定心部会与膛壁发生碰撞弹回的运动，导致弹丸并非沿身管轴线运动，而会与身管轴线产生一定的角度。同时可以看出，整个运动过程弹头部分较弹尾部分振动幅度大。弹丸运动阶段后期弹丸的俯仰和侧摆的运动相对之前较为剧烈。图9 中，由于大口径火炮的身管在自重状态下的挠度比较大，弹丸垂直方向的主运动受到了挠度很大的影响，而与图8 相比，弹丸运动中后期弹丸自身姿态变化所产生的扰动已体现的不太明显。图10 可以看出，弹丸由于前后定心部与膛壁的间隙碰撞弹回所产生的扰动速度极为剧烈，特别是在弹丸运动后期扰动速度急剧上升。从图11 可以看出，身管自重所引起的挠度影响了弹丸垂直方向的运动趋势。因此，身管的自重弯曲和弹炮耦合作用对弹丸飞行姿态的影响不可忽略。

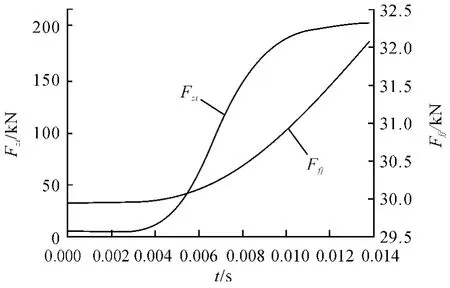
图5 用户子程序传递得到的反后坐装置力学特性

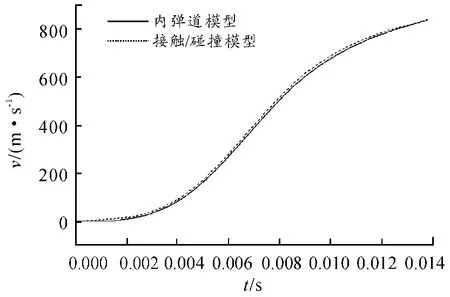
图6 弹丸质心沿身管轴线方向的速度

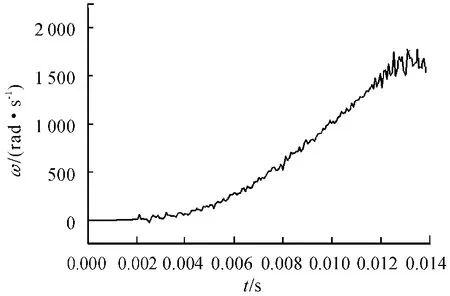
图7 弹丸质心沿身管轴线方向的角速度

图8 重力状态下弹丸相对地面的水平方向位移

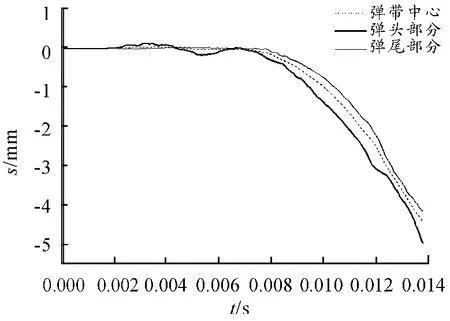
图9 重力状态下弹丸相对地面的垂直方向位移

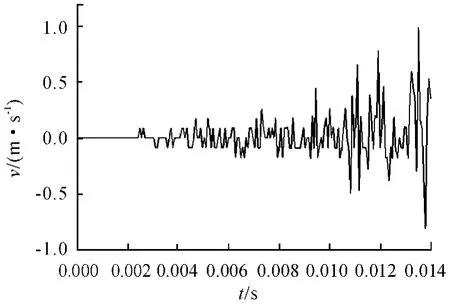
图10 重力状态下弹丸质心相对地面的垂直方向速度

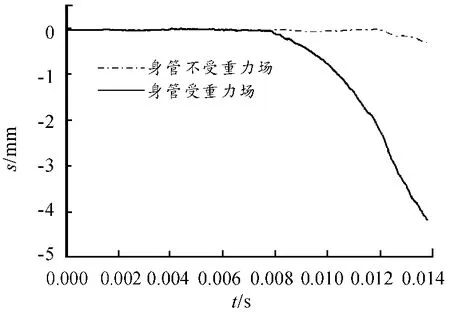
图11 弹带中心的垂直方向位移

6 结束语

本文利用弹塑性接触/碰撞有限元理论，建立了精确的身管和弹丸的有限元模型，利用有限元显式隐式混合计算方法模拟了在重力静态平衡下的火炮发射过程，解决了重力场在不同求解器间的稳定传递的问题，构建了显式函数用户子程序和子程序的数据传递来模拟弹丸膛内时期后坐体的后坐过程。考虑了膛线与弹丸的耦合作用对弹丸膛内运动的影响，研究了身管自重状态下弹丸膛内运动规律。为进一步深入研究弹炮耦合的全炮发射动力学打下一定的基础。

［1］康新中，吴三灵，马春茂.火炮系统动力学［M］. 北京:国防工业出版社，1999.

［2］葛建立，杨国来，陈运生.基于弹塑性接触/碰撞模型的弹炮耦合问题研究［J］.弹道学报，20(3):103-106.

［3］史跃东，王德石.考虑惯性效应的移动弹丸作用下身管振动特性［J］.兵工学报，2011，32(4):414-420.

［4］芮筱亭，杨启仁.弹丸发射过程理论［M］.南京:东南大学出版社，1992.

［5］姜沐，郭锡福.弹丸加速运动在身管中激发的振动［J］.弹道学报，2002，14(3):57-62.

［6］楚志远.自行火炮非线性有限元动力学仿真［D］.南京:南京理工大学，2001.

［7］蒋友谅.非线性有限元法［M］.北京:北京工业学院出版社，1988.

［8］程红梁.接触碰撞问题的算法研究［M］.南京:南京航空航天大学，2007.

［9］刘书，刘晶波，方鄂华.动接触问题及其数值模拟的研究进展［J］.工程力学，1999，16(6):14-28.

［10］魏惠之，朱鹤松，汪东晖.弹丸设计理论［M］.北京:国防工业出版社，1985:108-111.

［11］葛建立.车载炮动态非线性有限元仿真研究［D］.南京:南京理工大学，2009.

［12］赵金辉，何忠波，傅建平，等.火炮发射过程中身管温度场及弯曲度的有限元计算［J］. 火力与指挥控制，2011(5):106-109.