正轴测投影图直观效果优化条件的研究

徐越月， 林大钧

（华东理工大学，上海 200237）

与多面正投影相比，正轴测投影具有立体感强、直观性好、形象逼真等优点；与透视图相比，正轴测投影作图相对容易，度量也较方便；从影像反求角度看，由正轴测投影图反求物体三维模型也比由照片反求来得容易[1]。

正轴测投影立体感效果取决于平行光束与物体表面所形成的角度大小，其优化指标可根据所表达的对象在正轴测投影中显示的面的个数以及面积的大小和面积变化率等加以衡量。用面的个数标识正轴测投影表现物体的信息量，用面积的大小标识正轴测投影表现物体的信息量的丰腴程度，用面积的变化率则标识正轴测投影表现物体的变形程度。

1 可见面数的计算方法

当物体进行投影时，立体的每个平面的外法线N矢量与投影方向S之间有一夹角。当夹角大于或等于 9 0°时，表示平面背向投影方向或平行于投影方向，该平面不可见；当夹角小于 9 0°时，表示这个平面向着投影方向，该平面可见。

图1 凸面体表面外法线向量与投影向量关系

如图 1所示，S为投影方向，N为立体上ABCD面的外法线，沿ABCD面逆时针方向任取相邻两边作为两个向量AB、BC，这两个向量的叉积就是该表面的外法线 N的方向，即N = AB × BC。假设A、B、C点的坐标分别为坐标单位向量，可以得到

For i = 1 To NS

U1 = SV(S(i, 2), 1) - SV(S(i, 1), 1)

U2 = SV(S(i, 2), 2) - SV(S(i, 1), 2)

U3 = SV(S(i, 2), 3) - SV(S(i, 1), 3)

V1 = SV(S(i, 3), 1) - SV(S(i, 1), 1)

V2 = SV(S(i, 3), 2) - SV(S(i, 1), 2)

V3 = SV(S(i, 3), 3) - SV(S(i, 1), 3)

N(i, 1) = U2 * V3 - U3 * V2

N(i, 2) = U3 * V1 - U1 * V3

N(i, 3) = U1 * V2 - U2 * V1

If N(i, 2) > 0 Then k = k + 1

Next i

2 可见面积及变化率计算

面积变化率表征着可见面的变形程度，变形过大会导致图形严重失真。正轴测投影视觉上有立体感，但其本质是二维图形，所以显示的总面积可以通过每个显示面的像素和来衡量。在CAD中，正轴测投影图各点在Z轴方向上坐标皆为0，所以可以通过CAD中的area命令计算其面积，area命令的本质就是求封闭曲线内的像素点之和。

如图2所示，由于轴测投影图并不是单一的封闭曲线，CAD具有的功能只是通过在单一的封闭多线段内选取一点来形成面域，这在正轴测投影图中无法实现，所以先在轴测投影图周围设计一个矩形，该矩形辅助边界比轴测投影图的最小外围矩形大一个计量单位，这样可以使使图形成为辅助边界内的孤岛。在轴测图边框外围与矩形内侧选取一点，使用boundary命令在正轴测投影图的外围生成闭合边界多义线，然后应用(vla-get-area(vlax-ename->vla-object (car(entsel))))语句得到闭合区域的面积，即轴测图可视面的总面积。

图2 正轴测投影图外框示图

3 程序演示

运行时只需在文本框中输入旋转角度α、β，在 CAD中可以得到相应的正轴测投影图[4]，程序示例如图3所示。正轴测投影图的转换通过lisp编程实现，在程序中加入循环语句，可以大大减少程序的篇幅，具体如下：

(repeat 16

(setq x_set (car (eval(read (strcat "p" (rtos i))))))

(setq y_set (cadr (eval(read (strcat "p" (rtos i))))))

(setq z_set (caddr (eval(read (strcat "p" (rtos i))))))

(setq x_set_change (+ (* x_set S1x) (* y_set S1y) (* z_set S1z)))

(setq z_set_change (+ (* x_set S3x) (* y_set S3y) (* z_set S3z)))

(set (read(strcat "p" (rtos i) "_change")) (list x_set_change z_set_change))

(setq i (1+ i))

)

图3 程序示例

图2中所示正轴测投影图通过改变旋转角度α、β可以得到表1、2中的数据，其中表1反映了旋转角度α、β与可见面个数之间的关系，表2反映了旋转角度α、β与可见面变化率之间的关系。

表1 旋转角度与可见面之间个数的关系

表2 旋转角度与可见面面积变化率的关系

4 优化条件

面的个数、面积大小、面积变化率三者之间是相互抑制的，其中一个因素的变化可能会使另一个因素随之而变化，所以要在三者之间取得平衡，即图形的最佳表达方式。

要获得较好的直观效果，首先应避免面投影成线、线投影成点的现象[5]，图 4(a)的直观性就很差，同时应尽量使几何体的内部裸露出来，图4(b)应改变β角使凹槽面向视点。实验表明，合适的视角会使得对象显示面的数目较多，从而使反映的物体信息量更加丰裕，比较图4(c)与图2，可以看出图2的直观效果较好。由表1、2可以看出，当α、β在30°～60°之间时，显示面个数较多，且面积变化率百分比较大，同时各面大小比例比较均匀，这样更加符合人的视觉习惯。

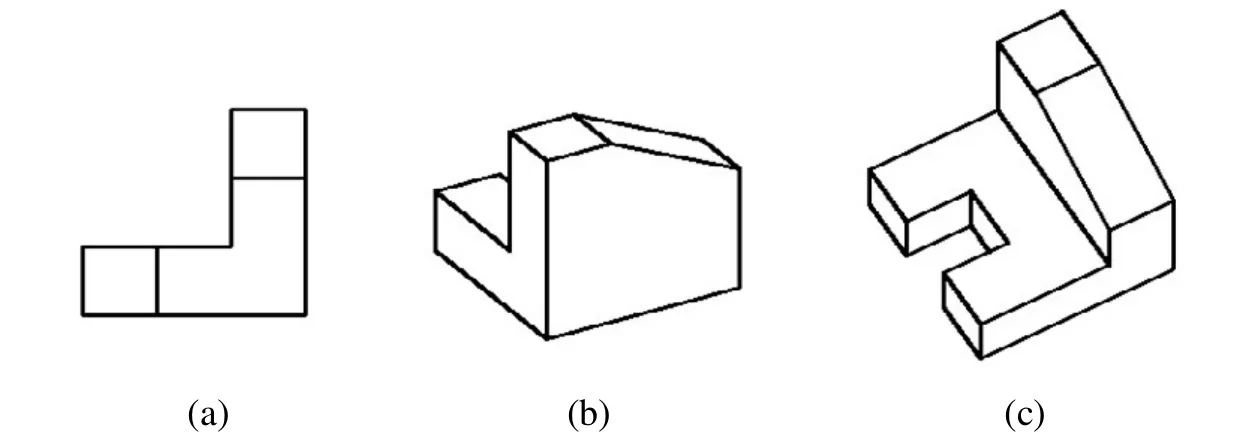
图4 图形示例

5 小 结

文章研究的是在已知投影角度的情况下，计算其投影面个数、大小以及变化率。根据研究结果可知工程上常用的基本视图是正轴测投影图的特殊情况，利用基本视图获得物体表面积计算比较繁琐，而利用正轴测投影图计算表面积则比较方便，可为计算物体表面积涂料用量、加工面积大小提供依据。

[1]韩素兰, 程 方. 常用轴测投影图在工程中的选择与应用[J]. 华北水利水电学院学报, 2005, 26: (4):76-78.

[2]陈锦昌. VB计算机绘图教程[M]. 广州: 华南理工大学出版社, 2003: 99-103.

[3]张晋西. Visual Basic.Net二次开发AutoCAD范例精解[M]. 北京: 清华大学出版社, 2004: 3-16.

[4]林大钧. 计算机工程图形算法及应用[M]. 上海: 华东理工大学出版社, 2006: 111-115.

[5]牛中原, 迟秋影. 理想正轴测投影作法[J]. 佳木斯大学学报(自然科学版), 2002, 20(4): 461-463.