轨道交通桥上无缝道岔群的受力分析

宫万国

（中铁第一勘察设计院集团有限公司，710043，西安∥工程师）

随着我国铁路建设的发展，受土地资源、地形地貌等因素影响，桥梁工程的比例越来越大，其中不乏车站设置于桥梁上的特殊情况，使车站咽喉区无缝道岔不可避免地设置于桥梁上［1－4］。为保证道岔的工作状态，一般将无缝道岔整组布置于连续梁上。对于客运专线大号码道岔咽喉区，由于道岔本身较长且布置多组道岔，由此引起多联大跨度连续梁集中布置的情况。图1是桥上车站咽喉区的典型布置情况。本文对普通桥上无缝线路及桥上无缝道岔群的受力进行了对比检算，分析了钢轨伸缩力分布特点及对桥跨布置形式的影响，对桥上无缝线路道岔设备轨条之间的相对位移和传力件强度进行了检算。

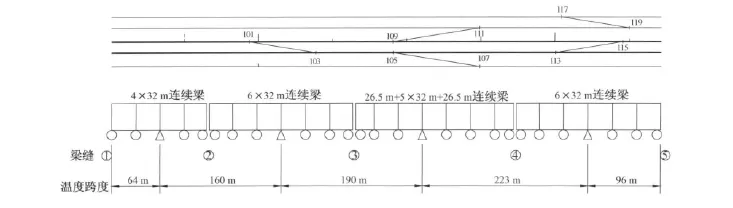
图1 桥上车站咽喉区的道岔及多联连续梁布置示意图

1 计算模型

由于桥上无缝道岔本身涉及多股道钢轨及各种限位结构共同作用，其计算模型较区间桥上无缝线路更为复杂，但两者的计算理论均可采用梁轨相互作用原理。本文采用通用有限元软件，分别建立普通区间桥上无缝线路和桥上无缝道岔有限元分析模型。无缝道岔群的布置形式如图1所示。模型中钢轨采用实体单元模拟，扣件纵向阻力采用弹簧单元模拟，道岔辙叉限位装置反力采用弹簧单元模拟，桥梁结构采用梁单元模拟，固定墩采用弹簧单元模拟。图2—图5是主要部件的有限元模型示意图。

图3 扣件阻力单元的有限元模型

图4 限位器单元的有限元模型

图5 间隔铁单元的有限元模型

2 计算参数

桥上无缝道岔及区间桥上无缝线路检算的物理参数如表1所示。

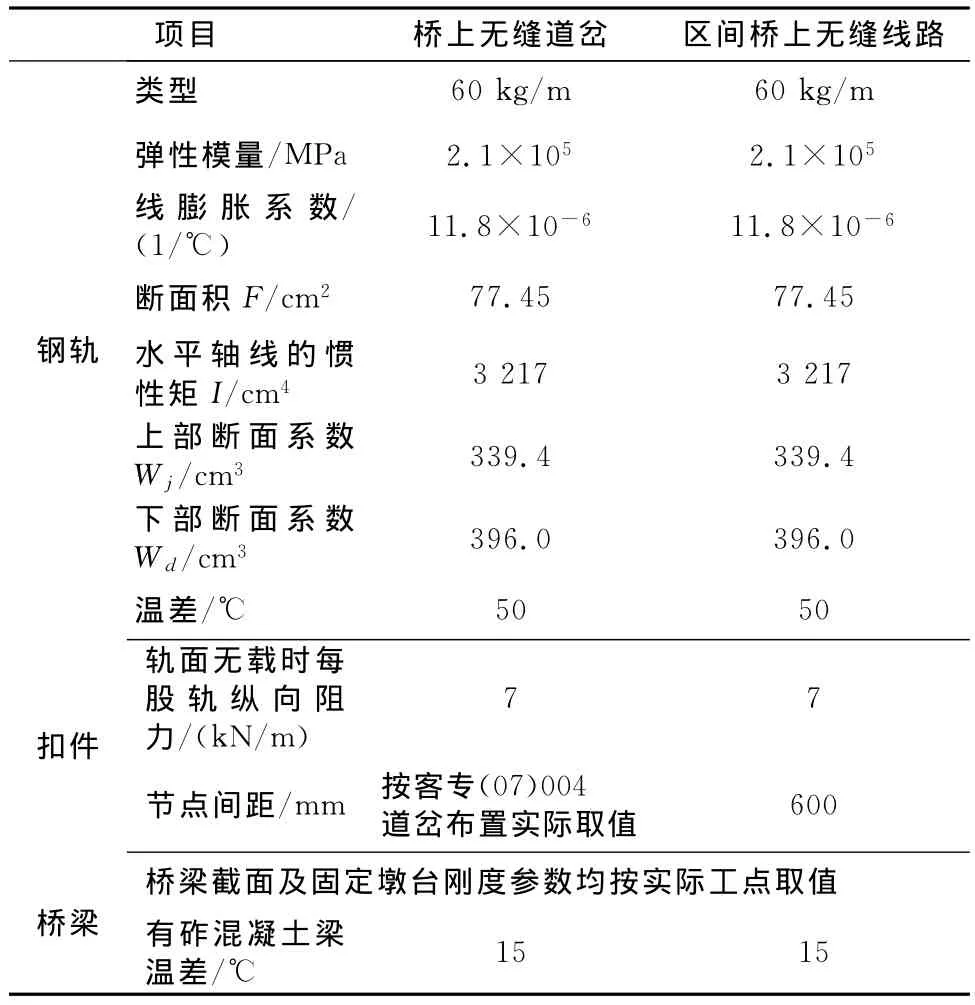
表1 计算参数

在有限元分析中，道岔限位器及间隔铁的阻力根据实测阻力曲线取值。道岔限位器和间隔铁的阻力曲线分别如图6、图7所示。由图6、图7可知：间隔铁子母块相对位移越大，阻力越大；当间隔铁子母块相对位移大于7mm后，限位器开始起限位作用。

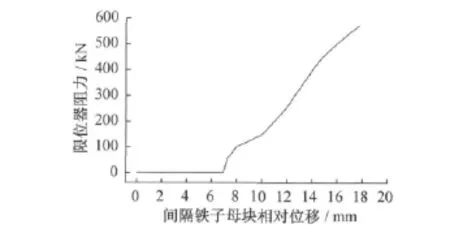
图6 道岔限位器阻力曲线

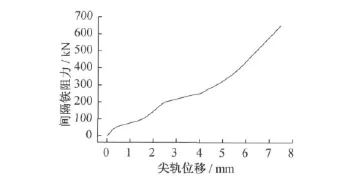
图7 道岔间隔铁阻力曲线

3 计算分析

3.1 钢轨伸缩力

无缝线路钢轨伸缩力的大小是无缝线路检算的重要内容，其数值大小除了与温度变化、轨道参数有关外，还受桥跨布置型式的影响。以下就普通区间桥上无缝线路和桥上无缝道岔两种不同的线路条件，采用上述有限元模型和计算参数，对钢轨伸缩力进行了对比计算分析。

3.1.1 普通区间桥上无缝线路

普通区间桥上无缝线路钢轨伸缩力分布如图8所示。由图8可见，钢轨伸缩力均值约为1 110 kN，受到①～⑤共5个桥梁梁缝的影响，伸缩力出现波动，并对应产生5个峰值，出现较大的伸缩附加力（即伸缩力的峰值－平均伸缩力）。

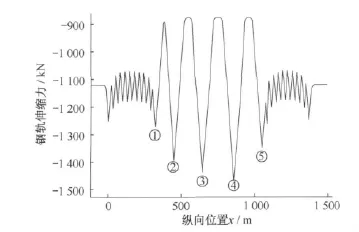
图8 普通区间桥上无缝线路单股钢轨伸缩力分布图

表2列出了各梁缝处的钢轨伸缩附加力P1及相应的附加应力最大值，表中数据表明，钢轨伸缩附加力变化范围在154.7～350.3kN之间，极大值出现在④号梁缝处。

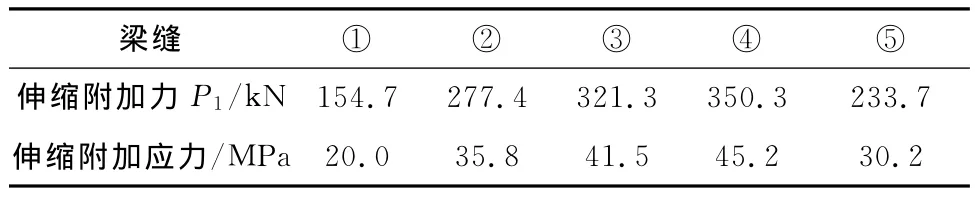
表2 梁缝处钢轨伸缩附加力及附加应力最大值表

3.1.2 桥上无缝道岔

通过对图1所示的桥上无缝道岔群的有限分析，道岔基本轨、辅助轨等多股钢轨的伸缩力分布如图9所示。与普通区间桥上无缝线路的计算结果类似，桥梁布置对桥上无缝道岔钢轨伸缩力的影响较大。表3列出了桥上无缝道岔在梁缝处的附加伸缩力P2和相应的附加应力最大值；为了便于比较，同时列出了P1与P2的比值。

分别比较图8、图9和表2、表3可见，桥上无缝道岔钢轨伸缩附加力最大值仍位于梁缝处。由于道岔尖轨限位器作用，梁缝附近布置道岔时的钢轨伸缩附加力较普通区间桥上无缝线路均有所增加。

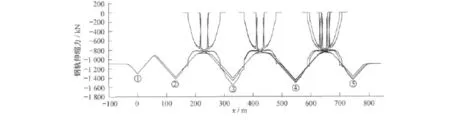
图9 桥上无缝道岔群各股钢轨伸缩力分布图

表3 梁缝处钢轨伸缩附加力及附加应力最大值表

普通区间桥上无缝线路钢轨伸缩附加力最大值（350.3kN）在桥梁温度跨度最大处（218.5m），而桥上无缝道岔钢轨伸缩附加力最大值（458kN）在103＃、105＃道岔之间的梁缝处（此处桥梁温度跨度为186.5m）。这主要是由于该处梁缝两侧的两组道岔对向布置，道岔尖轨钢轨附加力二次叠加，因此应在两连续梁间插入简支梁，以减少桥梁温度跨度，有效降低梁轨相互作用力。桥上无缝道岔钢轨伸缩附加力增幅最大处在⑤号梁缝（见表3），主要由于119＃道岔岔前距梁缝距离较小，桥梁伸缩及尖轨限位同时作用，叠加效果明显。由此可知，在设计中道岔距梁缝应保持一定距离，以尽量减少连续梁温度跨度与道岔限位装置钢轨附加力的叠加效应。

3.2 钢轨伸缩位移

由于道岔本身限位装置及线形要求，对基本轨相对桥梁和尖轨相对基本轨的位移均有相应限值。对图1所示的多联连续梁无缝道岔群，表4列出了道岔群设计所关心的钢轨、桥梁伸缩相对位移值。

由表4数据可见，尖轨相对基本轨的最大位移为23.7mm，满足CZ2602《时速250km客运专线铁路60kg／m钢轨18号道岔》中对道岔要求的限值30mm；心轨相对基本轨的最大位移为6.2mm，满足一般道岔要求的限值8mm。

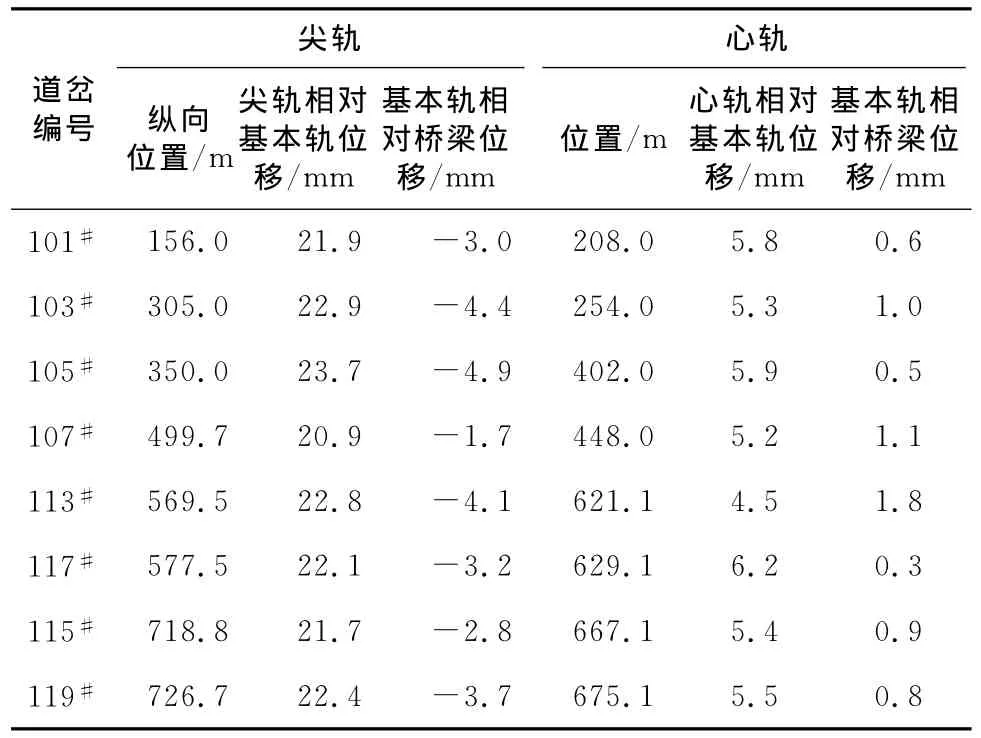
表4 桥梁钢轨伸缩相对位移表

3.3 道岔限位装置的剪力分析

道岔除了保证各轨条相对位移满足规范要求外，其传力件的剪力也必须满足强度要求。对于图1所示的多联连续梁上铺设的无缝道岔群，根据上述有限元模型，可计算出各道岔传力件的受力情况如表5所示。

表5数据表明，103＃、105＃道岔对向布置，直股、侧股等部位传力件的受力较大，其中最大值出现在105＃道岔的直股部位，达到155.7kN。现对其传力件螺栓的抗剪强度进行检算。

间隔铁受力螺栓剪应力为：

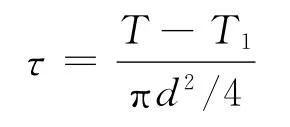
式中：

τ——间隔铁受力螺栓剪应力；

T——间隔铁受力螺栓剪力；

T1——摩阻力，取40kN／块；

d——螺栓直径，取24mm。

假定螺栓平均受力，辙跟处小间隔铁由2根螺栓组成，则由上式有：τ＝127.9MPa≤［τ］＝264MPa。所以，间隔铁螺栓的抗剪能力满足要求。

表5 道岔传力件受力表kN

4 结语

在高架桥上布置无缝道岔群的情况越来越多。本文针对一种典型的多联连续梁上铺设的无缝道岔群，采用有限元软件，对无缝道岔的温度力、相对位移和限位装置剪力进行了分析。计算结果表明：

1）无缝道岔布置于连续梁上时，其钢轨伸缩附加力较普通区间桥上无缝线路增幅较大，尤其是咽喉区设在多联连续梁上且两组道岔对向布置的情况最为不利。

2）若由于运输组织功能需求，道岔对向布置情况不可避免，此时应在两连续梁间插入简支梁，以减少桥梁温度跨度，有效降低梁轨相互作用力。

3）道岔距梁缝应保持一定距离，以尽量减少连续梁温度跨度与道岔限位装置钢轨附加力的叠加效应。

4）当整组无缝道岔布置于连续梁上时，道岔尖轨、心轨的位移及限位装置结构强度在一般情况下均可满足其限值要求。

［1］黄正华.合宁铁路无缝道岔群设计技术研究［J］.铁道工程学报，2009（6）：54.

［2］徐井芒，陈嵘.桥上无缝道岔纵向力计算研究［J］.铁道建筑，2011（3）：93.

［3］王平，刘学毅.无缝道岔计算理论与设计方法［M］.成都：西南交通大学出版社，2007.

［4］谭晓春，罗雁云.轨道交通列车过岔振动特性研究［J］.城市轨道交通研究，2008（1）：28.