基于OpenMP的短波射线追踪并行计算

王俊江，许利军，柳 文，焦培南

(1.中国电波传播研究所，山东 青岛 266071;2.电波环境特性及模化技术国家重点验室，山东 青岛 266071;3.新乡学院，河南 新乡 453003)

0 引言

短波射线追踪技术能够比较真实地反应无线电波在电离层中的传播轨迹，是研究电离层电波传播效应的有效工具，能够计算无线电波经过电离层到达目标的群路径、相路径、方位角、地面距离、反射高度、入射仰角和电离层传播模式等电波传播参数，在电离图反演、电离图合成等方面越来越受到不同学者的青睐［1～5］。数值射线追踪可以得到相当精确的计算结果，但计算量一般很大，很难应用到工程中。为了在精度和时间上取得一个均衡，人们研究了多种方法，但一般都是二维射线追踪并且做某种程度的简化，在文献［5，6］中给出了三维射线追踪的快速计算方法，但没有考虑在多CPU多核情况下的并行计算，经过检索尚未发现把并行化计算引入三维短波射线追踪的文献。

OpenMP并行计算技术是针对共享内存多处理器体系结构的可移植并行编程模型，能够支持并行计算时对线程和变量的灵活设计和控制。对比操作系统平台上的多线程编程步骤，应用OpenMP的过程更为简便［7，8］。近年来随着多核 CPU的不断发展，OpenMP已受到越来越多的重视。

从Hasgrove方程出发，实现了考虑地磁场情况下的三维射线追踪，利用多核处理器的计算机开展了短波三维射线追踪的OpenMP并行算法研究，并以准抛物电离层模型为例进行仿真计算。仿真结果证明了该算法的有效性，展示了该算法的应用前景。

1 三维数字射线追踪的方法原理［5］

1.1 三维数字射线追踪方程

在球坐标系中，以电波传播群路径P'为参数的射线方程可描述为

式中，P'为群路径;r、θ、φ是射线路径上的点在球坐标系中的坐标;kr、kθ、kφ是波矢量在球坐标系中的三个分量;c为光速。式(1)～(6)用于计算射线路径上点的坐标及在该点处的波矢量，式(7)计算时变介质中电磁波的频率漂移。由电离层的时变性造成的频率漂移量很小，在计算射线参数时可以忽略不计，因此，无需在射线追踪的每一步对频率进行调整。

H为哈密顿算符，Haselgrove引入的哈密顿算符与波矢量、相折射指数的关系为

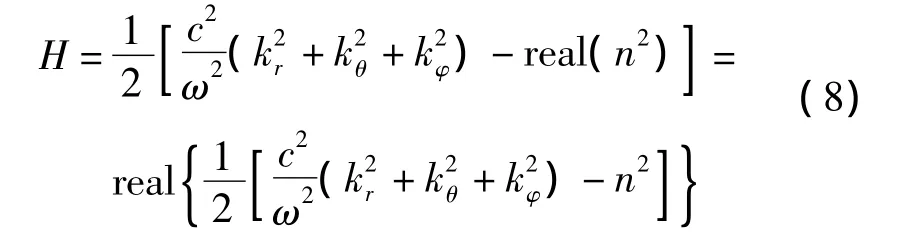
式中，n为相折射指数，在考虑磁场和碰撞的情况下，折射指数为

1.2 方程的数值解法

利用常微分方程组的数值解法求解上述射线微分方程组，群路径每变化一个步长，便可得到射线路径上不同点处的波矢量及坐标矢量，最终形成完整的射线描迹，得到传播路径的主要参数，如群路径、地面距离和方位偏差等。

本文采用了标准的龙格-库塔(Runge-Kutta)方法进行计算。

2 并行算法设计

2.1 OpenMP线程并行设计

在使用龙格-库塔法进行三维射线追踪时，由于每计算一步都需要上一步的计算结果，因此每一条射线只能串行求解。在使用射线追踪时，频率和仰角按一定的步进扫描进行，此时可以采用OpenMP指令以增加并行性。

OpenMP是基于派生/连接(fork/join)的编程模型。一个OpenMP程序从单个线程开始执行，在程序的某些点需要并行执行时，程序派生出额外的线程，组成一个线程组。这些线程在一个称为并行区域的代码区中并行执行。线程到达并行区域的末尾时等待，直到整个线程组都到达，然后它们连接在一起，只有初始或者主线程继续执行，直到下一个并行区域(或者程序结束)OpenMP并行处理流程，如图1所示。

图1 OpenMP并行处理流程

OpenMP具有两个特性:串行等价性和递增并行性。当一个程序无论是使用一个线程运行还是使用多个线程运行时，它能够产生相同的结果，则该程序具有串行等价性。在大多数情形中，具有串行等价性的程序更易于维护和理解。递增并行性是指一种并行的编程类型，其中一个程序从一个串行程序演化为一个并行程序。处理器从一个串行程序开始，一块接着一块的寻找值得并行执行的代码段。这样，并行性被逐渐添加。在这个过程的每个阶段，存在一个可以被验证的程序，这极大地增加了项目的成功机率。

在并行设计的过程中，尤其要分析程序的串行等价性，注意全局变量、在多个地方更改的类的成员变量和类的指针成员变量等。

2.2 短波射线追踪并行化程序分解

通过在短波射线追踪算法中增加OpenMP编译指令实现算法的并行化。射线追踪的一般过程为

循环变量为私有变量，在一次射线追踪中，数值算法的变量、计算返回的结果等，都为私有变量。

以下为计算多个频率多个仰角做射线追踪的例子代码。

其中CRaytrace为射线追踪类，里面封装了数值计算，各种电离层模型、地磁场模型和碰撞模型的计算等。在并行化计算中，必须把该类的对象定义为私有。

3 仿真运行实例及结果分析

3.1 仿真测试的基本原则和方法

为了检测短波射线追踪并行程序的正确性和效率，采用在同等条件下(同一机型和同一模型)并行程序和串行程序进行对比计算的方法。如果并行程序和串行程序计算结果完全相同或者满足精度要求，则可确认并行程序是正确的。对于并行效果，一般用并行加速比来度量。通常并行加速比可以定义为串行执行时间与并行执行时间之比，即

3.2 测试结果及分析

目前，准抛物电离层电子浓度模型［9，10］得到了广泛的应用，其等离子体频率fN随高度的分布可描述为如下的函数形式

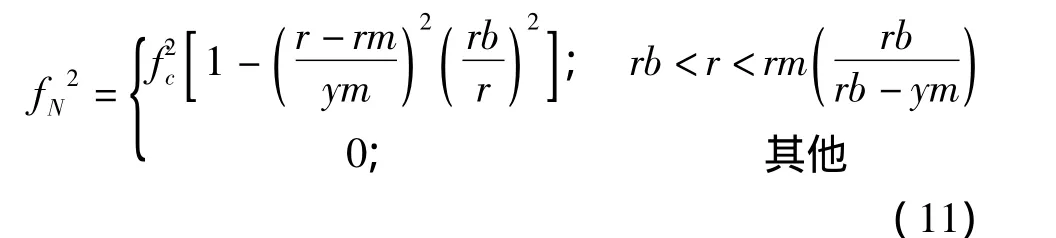
式中，rm为从地心算起的最大电子浓度对应的高度，单位为km;rb为从地心算起的电离层底高，单位为km;ym=rm－rb为电离层半厚，单位为km;fc为电离层的临界频率，单位为MHz。

以准抛物模型返回散射电离图合成为例进行了对比分析。其中单层准抛物模型参数为fcF2=6 MHz、rbF2=100 km、rmF2=200 km;两层准抛物模型的参数为 fcE=3 MHz、rbE=85 km、rmE=100 km、fcF2=6 MHz、rbF2=150 km、rmF2=250 km;三层准抛物模型的参数为fcE=3 MHz、rbE=85 km、rmE=100 km、fcF1=5 MHz、rbF1=120 km、rmF1=150 km、fcF2=8 MHz、rbF2=170 km、rmF2=250 km。运算平台为4核Intel酷睿2CPU，4 G内存。

在此两种参数下分别运行串行和并行实例，得到的运行结果完全一致，计算结果如图2、图3和图4所示。计算运行的时间见表1，由该表可以看出在4核的计算机上，加速比大于3，计算效率约80%，运行速度得到大幅度提高。

图2 单层准抛物模型返回散射电离图合成

表1 并行程序与串行程序的运行效率比较

4 结语

多核架构的计算机及多核并行计算技术的快速发展为短波射线追踪的大规模工程应用打下了基础。通用利用OpenMP的并行计算技术，使运行速度得到了大幅度的提高，展示出在工程应用中的广阔前景。

［1］CROFT T A.Exact Ray Calculations in a Quasi-parabolic Ionosphere with No Magnetic Field［J］.Radio Sci.，1968，3(1):69-74.

［2］NORMAN R J.A Two-dimensional Analytic Ray Tracing Technique Accommodating Horizontal Gradients［J］.Radio Sci.，1997，32(2):387-396.

［3］DAVIES K，RUSH C M.High-frequency Ray Paths in I-onospheric Layers with Horizontal Gradients［J］.Radio Sci.，1985，20(1):95-110.

［4］KELSO J M.Ray Tracing in the Ionosphere［J］.Radio Sci.，1968，3(1):1-12.

［5］柳文，焦培南，王世凯，等.电离层短波三维射线追踪及其研究［J］.电波科学学报，2008，23(1):41-48.

［6］柳文，王俊江，焦培南，等.电离层三维射线追踪的快速计算方法［J］.电波科学学报，2009，24(1):55-59.

［7］OpenMP Application Program Interface［J/OL］.http://www.openmp.org/mpdocuments/spec30.pdf，(2008-06-02).

［8］张林波，迟学斌，莫则尧，等.并行计算导论［M］.北京:清华大学出版社，2006.

［9］HASELGROVE J.Ray Theory and a New Method for Ray Tracing［C］//Physics in the Ionosphere.London:Proc.Phys.Soc.，1955:355-360.

［10］JONES R M.A Three-dimensional Ray-tracing Computer Program［J］.Radio Sci.，1968，3(1):93-94.

［11］索玉成.电离层短波射线追踪［J］.空间科学学报，1993，13(4):306-312.

［12］李妮，陈铮，龚光红，等.多核并行计算技术在景象匹配仿真中的应用［J］.系统电子工程与电子技术，2010，32(2):428-432.