吸附式压气机叶型优化设计

刘波，李俊

（西北工业大学动力与能源学院，西安 710072）

吸附式压气机叶型优化设计

刘波，李俊

（西北工业大学动力与能源学院，西安 710072）

刘波（1960），男，教授，博士生导师，研究方向为叶轮机气动热力学。

将微分进化算法和流场数值模拟技术相结合，建立了1套吸附式压气机叶型智能优化系统。此系统可以对进口亚声、超声的吸附式压气机叶型进行优化。通过准3维叶栅通道计算程序-MISES进行流场数值模拟，评估叶型气动性能。选取吸附式叶型最重要的2个变量，吸气量和吸气位置作为优化参数，以叶型的损失系数作为优化目标，自动寻优找到该叶型的最佳吸气量和对应的吸气位置。数值计算结果表明：优化后的吸附式叶型的气动性能有了明显的提高。

吸附式压气机;叶型优化；吸气量；吸气位置；智能优化

0 引言

现代航空发动机的压气机必须满足新的设计需求：高压比、低级数、高效率。压气机级数的减少会造成每级负荷的增加[1-4]；附面层在高逆压梯度下更易发生气流分离现象，造成发动机损失的增加以及性能的下降。许多学者近期做了大量的工作，研究高负荷条件下的流动控制技术，抑制附面层在高负荷下的分离；而附面层抽吸技术是目前实现目标的最有效方法[5-6]。Merchant和Schuler分别设计并验证了具有较高性能和负荷的采用附面层抽吸的压气机级，前者叶尖速度为457m/s时压比为3.4，动叶和级效率分别为93%和86%；后者叶尖切向马赫数为0.7时压比为1.6，动叶和级效率分别为96%和90%[7-9]。从目前的研究结果来看，吸附式压气机的可行性和应用前景已经得到了国内外研究者的认可，相关研究正朝着更广泛、更深入的方向发展，尤其是最佳的吸气量和吸气位置是目前研究的热点[10]。Merchant认为吸气量以及吸气位置的选择对于吸附式压气机叶型的设计具有重要的意义，而且Merchant和Schuler进行试验之前对吸气量和吸气位置在准3维设计阶段均进行了优化[11-13]。国内很多学者也对这个问题进行过研究，张华良、兰发祥等人都对最佳吸气量和吸气位置进行过研究，进行了大量的工作，得到了一些如何找寻最佳吸气量和吸气位置的方法和经验[14-16]。然而，这种人为的手动的进行多工况的寻找，既浪费时间，又不一定能精准的找到最佳的吸气方案。

本文建立1种将计算机优化算法和流场数值模拟技术相结合，智能寻找叶型最佳吸气方案的优化系统。

1 优化算法

微分进化算法（DE）作为吸附式压气机叶型寻找最佳吸气量和吸气位置优化算法。微分进化算法是美国学者Storn和Price于1995年提出的1种模拟“优胜劣汰，适者生存”的自然进化法则的仿生智能计算方法。此算法在解决复杂的全局优化问题方面的性能更加突出，过程也更为简单，受控参数少，被视为仿生智能计算产生以来在算法结构方面取得的重大进展。Storn和Price在其研究报告中称，微分进化算法在收敛速度和稳定性方面都超过了其他几种知名的随机算法，如退火单纯形法、自适应模拟退火算法、进化策略和随机微分方程法。作为1种基于群体进化的仿生智能计算法，具有记忆个体最优解和种群内部信息共享的特点，即通过种群内个体的合作与竞争来实现对优化问题的求解。算法本质上可看做是1种基于实数编码的、具有保优思想的贪婪遗传算法。此算法的基本操作包括变异、交叉及选择3种操作。整个优化系统的运行流程如图1所示，在计算迭代中，随机选择2个不同的个体向量相减产生差分向量，然后将差分向量赋予权值后与另1个随机选出的向量相加，从而生成变异个体；变异与目标个体进行参数混合交叉，得到交叉个体，然后对交叉个体与原目标个体进行一对一的选择，择优生成新一代的种群[17]。

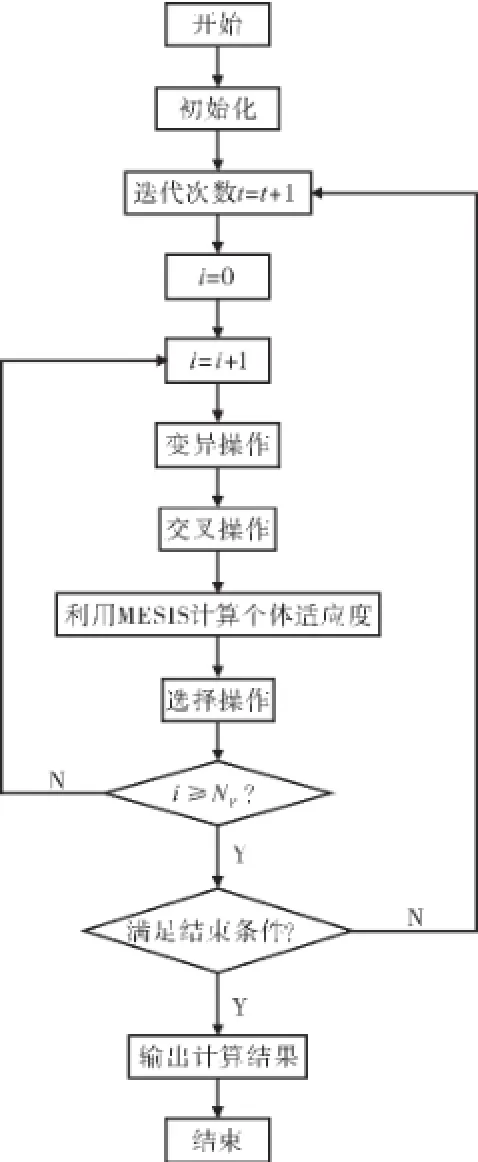
图1 整个优化系统的运行流程

其中：t为循环次数；i为目标个体索引号；NP为初始化种群规模。

2 流场计算方法

采用MIT研发的MISES程序作为求解亚声、超声吸附式叶栅内部黏性流动的数值模拟方法。MISES程序最初由Mark Drela编写，用于稳态S1流面流场计算，后来AliMerchant在程序中添加了抽吸模块，用于吸附式叶型设计与计算。在2000年，Ali Merchant、Jack L.Kerrebrock等人用MISES程序设计了1台压比为3.5，叶尖速度为457 m/s的吸附式风扇级[18]，并在2005年进行了试验[12]，试验结果与设计指标基本相吻合。在MISES程序中，按照位移厚度，把流场分为边界层内黏性流场和外无黏流场2个区域，进行耦合迭代计算。迭代计算过程中，首先，把整个流场当作无黏流场使用欧拉方程组求解，然后，根据欧拉方程组所解边界上的速度以及边界层内的积分方程，求得边界层位移厚度等参数，根据所求得的边界层位移厚度划分新的无黏流场区域求解欧拉方程组，再求得新边界层位移厚度，直到前后2次所求边界层位移厚度误差达到计算精度，迭代收敛为止。主流无黏区域采用欧拉方程组求解，黏性边界层区域采用卡门动量积分方程和能量积分方程求解。

边界层外的欧拉方程如下：

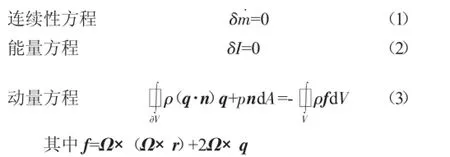
边界层内的积分方程如下：

卡门动量积分方程

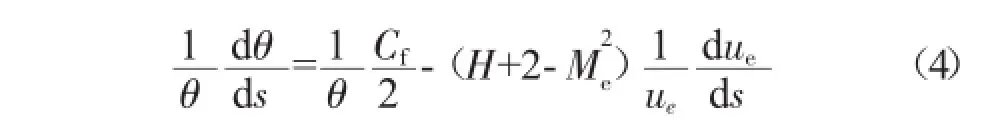
能量积分方程

式中：m˙为质量流量；ρ为密度；q为绝对速度；n为边界上法向向量（以指向外为正）；Cf为摩擦系数；s为流向坐标；θ为动量厚度；H为形状因子（δ*/θ）；H*为形状因子（θ*/θ）；H**为形状因子（θ**/θ）；θ*为能量厚度；θ**为密度厚度。

分别选取某2级风扇在110%转速下，第1级转子根部叶型（叶型1）和自主设计大弯角叶型（叶型2）作为优化对象。由于工作在110%转速下，转子全叶高超声，因此叶型1为超声叶型，进口马赫数为1.1，进气角为51.34°，计算总网格数为266×20，网格如图2所示。叶型2为大弯角亚声叶型，进口马赫数为0.7，叶型弯角为70°，进气角为49.76°，计算总网格数为343×20，网格如图3所示。

图2 叶型1初始计算网格和不吸气计算收敛后网格

图3 叶型2初始计算网格和不吸气计算收敛后网格

3 结果分析及讨论

在没有抽吸的情况下的，计算叶型的损失为0.1271（如图4所示），叶栅通道中存在1道很强的通道激波，激波与吸力面相碰于大约40%弧长位置，激波后吸力面附面层急剧发展，位移厚度和形状因子急剧增大，摩擦系数急剧减小，很快便出现分离，分离位置在54%吸力面弧长处（以摩擦系数减小到0为判断标准）。

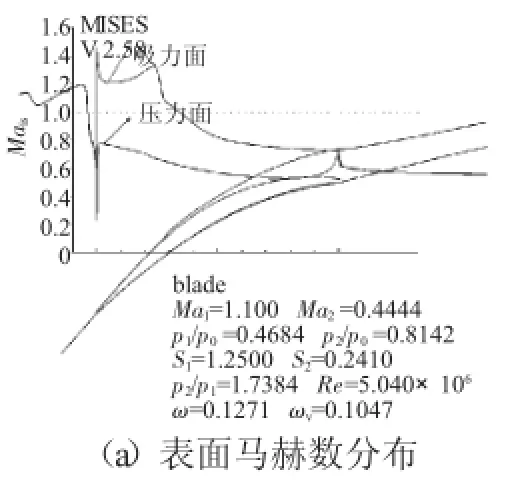
图4 叶型1不吸气时计算结果

在优化前由于分离位置在54%弦长处，因此将抽气位置定为0.60～0.62（相对弦长位置，本文中抽气位置均在吸力面），抽吸量为0.5%，计算叶型的损失为0.0748，在优化后抽气量为0.5%，抽气位置为0.43～0.45，计算叶型的损失为0.0575。如图4（a）所示，激波位置大约在40%弦长处。如图5～7所示，优化前抽吸位置位于分离区内，附面层已充分发展，抽吸虽然叶型损失有所降低，但是抽吸位置仍有低能流体分离。优化后，抽吸位置在激波后，分离起始位置，附面层尚未充分发展，可以很好的对附面层进行控制。优化后低形状因子段占整个弦长的比例有了明显的增加，优化后吸力面位移厚度和动量厚度有了明显的减小。优化后尾缘处摩擦系数为零的区域明显减少，基本消失。优化后损失系数降低的比较明显，比优化前减小了大约25%。特别是优化之后的黏性损失，从优化之前的0.0446减小到0.0251，减小了大约44%，这说明抽吸的优化对于附面层的控制非常重要，合理的抽吸位置会使附面层的损失下降非常明显。

图6 叶型形状因子分布

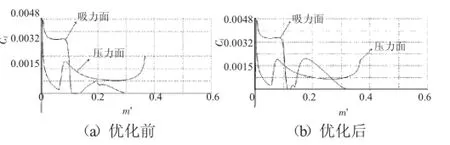
图7 叶型摩擦系数分布

3.2 叶型2优化前后对比

该叶型的弯角达到了70°，具有很高的负荷。在没有抽吸的情况下的，计算叶型的损失为0.0505，附面层在叶型前段一直附着良好（如图8所示）。在80%弦长处附面层开始恶化，形状因子急剧上升，摩擦系数也减小为零，附面层发生分离。

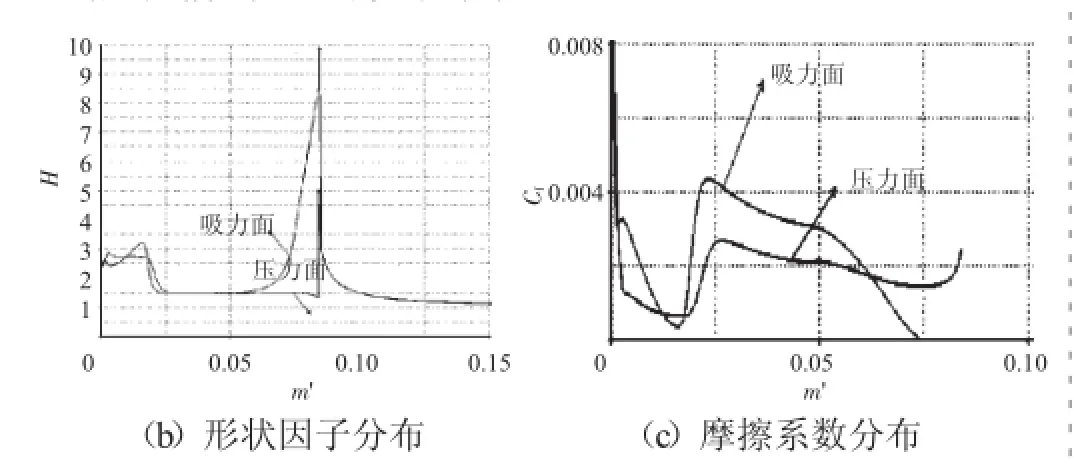
图8 叶型2不吸气时计算结果

图9 叶型表面马赫数分布

图10 叶型形状因子分布

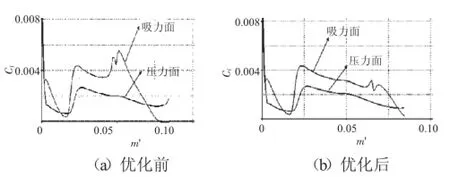
图11 叶型摩擦系数分布

在优化前抽吸量为1%，抽气位置为0.60～0.62，计算叶型的损失为0.0272，在优化后抽气量为1%，抽气位置为0.78～0.80，计算叶型的损失为0.0177。如图9～11所示，优化前虽然较之抽吸前叶型的附面层状况已经有了很大的改善，分离的区域明显减小，损失下降也比较明显，但是在叶型的尾缘处附面层依然发生了分离，这会对叶型造成很大的损失，而在优化之后，形状因子有了明显的下降，基本都保持在3.0以下，摩擦系数为零的区域全部消失，证明在优化之后附面层的分离全部消除，叶型性能显著提升。优化后较优化前损失减小了为35%，具有明显的优化效果。该叶型在不同攻角下，优化前与优化后的攻角特性（如图12所示）。在-2～4°的攻角范围内，较之优化前，优化后的吸附式叶型具有更小的损失，而且各个工况下损失下降的均很明显，说明优化在不同攻角特性下效果保持良好。

图12 叶型攻角特性

4 结论

（1）发展了1套将微分进化算法和流场数值模拟技术相结合的吸附式压气机优化设计系统，针对进口亚声和超声吸附式压气机叶型进行优化。通过准3维叶栅通道计算程序MISES评估叶型气动性能，系统智能化寻优，得到吸附式压气机叶型最佳的吸气位置和吸气量。

（2）对某2级风扇第1级转子超声叶型进行了优化，并对自主设计的大弯角亚声叶型进行了优化。数值计算结果证明：优化之后，找到了叶型的最佳抽吸位置和抽吸量。叶型的最佳抽吸位置位于分离起始位置，抽吸位于分离区不能很好的控制附面层的分离。优化后抽吸的效果明显得到了改善，叶型的损失系数大幅度的减小，湍流附面层的发展得到了很好的控制，叶型表面的分离基本消除。2个叶型的气动性能均有了明显的改善，证明了本文建立的吸附式压气机叶型优化设计系统不仅具有很好的效果，而且具有较强的可靠性。

[1]Godard A,Fourmaux A,Burguburu S,et al.Designmethod of a subsonic aspirated cascade[R].ASME 2008-GT-50835.

[2]Liesner K,Meyer R,Lemke M,et al.On the efficiency of secondary flow suction in a compressor cascade[R].ASME 2010-GT-22336.

[3]Gmelin C,Thiele F,Liesner K,et al.Investigations of secondary flow suction in a high speedcompressor cascade[R].ASME 2011-GT-46479.

[4]Wennerstrom A J.Highly loaded axial flow compressors：history and current developments[J].Journal of Turbomachinery,1990,112(10)：567-578.

[5]Godard A,Bario F,Burguburu S,et al.Experimental and numerical study of a subsonic aspirated cascade[R].ASME 2012-GT-69011.

[6]Lord W K,MacMartin D G,Tillman T G.Flow control opportunities in gas turbine engines[R].AIAA-2000-2234.

[7]Schuler B J,Experimental investigation of an aspirated fan stage[D].Boston：Massachusetts Institute of Technology,2001.

[8]Merchant A A.Design and analysis of axial aspirated compressor stage[D].Boston：Massachusetts Institute of Technology,1999.

[9]宋彦萍，陈浮，赵桂杰，等.附面层吸除对大转角压气机叶栅气动性能影响的数值研究[J].航空动力学报，2005，20（4）：561-566.

[10]陈绍文，郭爽，陆华伟，等.超高负荷吸附式压气机叶栅气动性能分析[J].热能动力工程，2009，24（2）：167-171.

[11]Merchant A A.Aerodynamic design and perfomance of aspirated airfoils[J].Journal of Turbomachinery,2003，125（1）：141-148.

[12]Merchant A A,Kerrebrock J L,Adamczyk J J,et al, Experimental investigation of a high pressure ratio aspirated fan stage[J].Journal of Turbomachinery,2005，127（1）：43-51.

[13]Schuler B J,Kerrebrock J L,Merchant A A.Experimental investigation of a transonic aspirated compressor[J].Journal of Turbomachinery.2005，127（4）：340-348.

[14]张华良，谭春青，张新敬，等.采用附面层抽吸（BLS）控制流动分离的数值模拟[J].推进技术，2009，30（2）：192-196.

[15]兰发祥，黄国平.吸附式压气机平面叶栅数值模拟研究[J].燃气涡轮试验与研究，2009，22（4）：1-8.

[16]刘波，南向谊，陈云永.附面层抽吸对转子激波结构和分离流动的影响[J].航空学报，2008，29（2）：315-320.

[17]段海滨，张翔银，徐春芳.仿生智能计算[M].北京：科学出版社，2011：107-116.

[18]Merchant A A,Drela M,Kerrebrock JL,et al.Aerodynamic design and analysis of a high pressure ratio aspirated compressor stage[R].ASME 2000-GT-619.

Optim ization for Aspirated Com p ressor Airfoil

LIU Bo,LIJun
（SchoolofPowerand Energy,NorthwesternPolytechnicalUniversity,Xi'an710072,China）

An intelligent optimization system for aspirated compressor airfoils was developed,which combined differentialevolution algorithm and numericalsimulationmethod of flow field.The inlet subsonic and supersonic aspirated compressor airfoilswere optimized by the system.The flow field was simulated by quasi-three dimensional cascade calculation programme-MISES and the aerodynamic performance wasevaluated.Themost importantsuction air flow rate and the suction location were regarded as optimization parameters.The profile loss coefficient were regarded as optimization goal.The best suction location and suction air flow rate for aspirated compressor profileswere automatically searched.The numerical calculation results show that the aerodynamic performance of the optimized aspirated compressor profilesareobviously improved.

aspirated compressor;airfoils optimization;suction air flow rate;suction location;intelligentoptimization

国家自然科学基金（50976093）资助

2012-09-14