远距引导战斗机自动攻击控制律实现

韩 庆， 魏贤智， 张 斌， 杜永伟

(空军工程大学工程学院，西安 710038)

0 引言

随着战斗机和先进机载武器的发展，对于战斗机的指挥引导技术要求也愈来愈高。先进的指挥引导系统是提高战斗机作战效能，实施精确打击的基础，在现代战争中具有广阔的应用前景［1-2］。先进的指挥引导系统不仅是对战斗机实施战前指挥引导［3-4］的必要前提，也是研制自动攻击控制律的必然要求。当前，技术的不断发展使得机载武器、传感器和战斗机本身性能得到了不断提高，现代空战的空间范围也不断扩大，目标、武器以及战斗机之间的相互关系也变得越来越复杂。传统的依靠飞行员操控战斗机实现引导和瞄准任务的方式由于对飞行员本身素质要求较高且操控任务繁重，不利于空战过程中飞行员对空战态势的判断，为了减轻驾驶员负担，提高空战效能，研制综合化、智能化、自动化的战术指挥引导系统也就势在必行［5］。

基于此，本文建立了战斗机引导的三维数学模型，引入了战斗机自动攻击的概念，将三维引导问题分解为水平和垂直两个平面分别进行研究，重点给出了水平面的引导原理推导过程;在综合考虑战斗机指挥引导过程中对相关性能参数要求的前提下，对时间最优引导的远距引导算法进行了实例仿真验证，并将战斗机引导过程中的飞行控制参数分离出来送给战斗机的飞控系统，从而实现了战斗机远距引导的自动攻击。

1 战斗机引导自动攻击及三维数学模型

1.1 自动攻击概念

本文主要研究的是单机向目标远距引导过程中自动攻击的实现，解决的是战斗机如何以飞行时间最短或能量消耗最少、面临的威胁最小为要求，迅速接敌。

基于此，为使问题表述准确，引入自动攻击概念，即:战斗机通过一定的引导律，满足引导过程中对相关参数要求的前提下，将引导过程中战斗机的飞行控制参数分离出来送给战斗机的飞控系统，飞控系统根据飞行控制参数自动驾驶战机对目标进行攻击的过程。借鉴某型战机在远距引导状态下自动引导的原理，对于远距引导部分，战斗机的飞控参数为战斗机飞行高度H，飞行速度V，飞行航向ψ。远距引导自动攻击原理见图1。

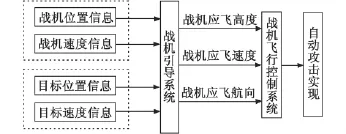
图1 远距引导自动攻击原理Fig.1 Fighter control law of long-distance guidance and auto-attack

1.2 战斗机引导三维数学模型

对于三维引导问题，通常将它描述为两个互相垂直的二维平面问题来研究［6-7］。本文中选取“北、东、地”地理坐标系(OXYZ)e来建立战斗机、目标的相对运动方程。就三维空间而言，被引导战斗机与目标的相对位置关系如图2所示。

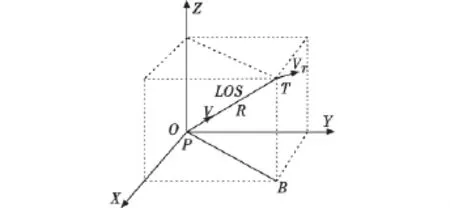
图2 战斗机与目标的三维位置关系Fig.2 Three-dimensional position of fighter plane and target

图中:P为战斗机;T为目标;R为战斗机与目标的距离;LOS为目标线;V，VT分别为战斗机和目标的运动速度。假设此时已经知道了战斗机的初始位置坐标xp，yp，zp;目标的初始位置坐标xT，yT，zT;战斗机的初始速度 VXP，VYP，VZP;目标的初始速度 VXT，VYT，VZT。

将战斗机三维引导问题转化为水平面OXY和垂直面OZB内进行研究。

则水平面内战斗机、目标的速度为

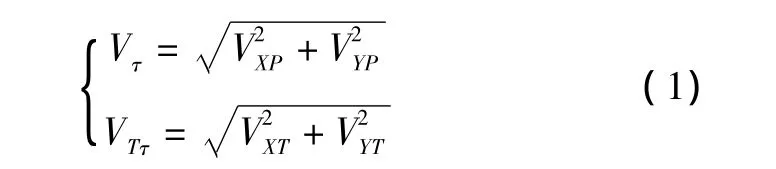
垂直面内战斗机、目标的速度为

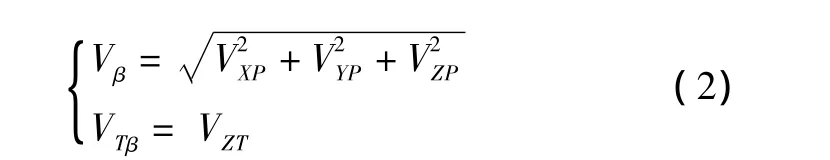
以水平面OXY分析战斗机、目标的相对运动方程。如图3所示。

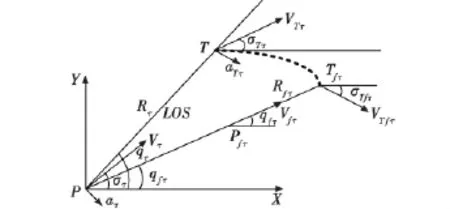
图3 战斗机与目标水平面位置关系Fig.3 Horizontal position of fighter plane and target

图中:Rτ为战斗机与目标的水平面距离;Vτ，VTτ分别为战斗机和目标水平面内的运动速度;qτ为目标线与基准线之间的水平面夹角;στ，σTτ是战斗机和目标进行远距引导水平面内的飞行航向角。Pfτ，Tfτ，Rfτ，Vfτ，VTfτ，qfτ，θTfτ为末端时刻战斗机、目标的运动参数。

则战斗机、目标水平面相对运动方程的极坐标描述为

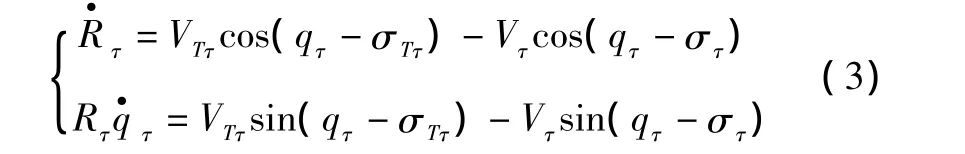
对于OZB垂直面，现给出平面内战斗机、目标的相对位置关系如图4所示。

图4 战斗机、目标垂直面位置关系Fig.4 Vertical position of fighter plane and target

图中:Rβ为战斗机与目标的垂直面距离;Vβ，VTβ分别为战斗机和目标垂直面内的运动速度;qβ为目标线与基准线之间的垂直面夹角;θβ，θTβ分别为垂直面内的战斗机速度矢量的前置角与目标速度矢量的前置角;εβ为目标垂直面内的进入角;σβ，σTβ是战斗机和目标在垂直面内的航向角。

最后得到战斗机、目标在垂直面内的相对运动方程组为

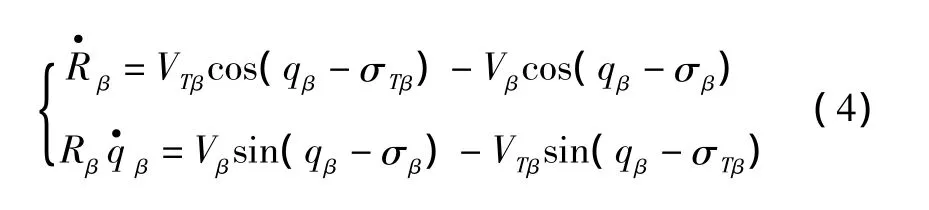
2 战斗机远距引导律

2.1 战斗机远距引导原理

研究地面指挥所或预警机指挥引导战斗机飞向目标，引导策略的核心问题是战斗机跟踪目标的引导律［8］。将战斗机远距引导至目标空域，所设计的引导律应以战斗机飞行时间最短或能量消耗最少、面临的威胁最小为目标，使战斗机迅速接敌。为此可以运用最优控制进行研究，并以计算机仿真手段进行验证。当地面指挥所或预警机发现有敌机来犯时，距离较远时战斗机先进行远距引导，对敌机进行拦截。远距引导是在战斗机火控系统通过地面指挥所或预警机获得目标的信息后，采用最优引导律远距截获目标的过程。当战斗机与目标的距离小于机载雷达自身的最大探测距离时，则战斗机雷达开机获取目标信息并转入近距引导。

远距引导要求引导律简单，易于实现，对引导精度要求较低。在此过程中，为了隐蔽起见，战斗机雷达处于关闭状态。如何引导战斗机到指定空域，并保持一定的态势优势，是远距引导所要解决的主要问题。

2.2 战斗机远距引导律

依据战斗机速度矢量与目标视线所要求的相对方向不同，战斗机引导方法可分为追踪法、固定前置角法、平行接近法和比例引导法［9-10］。追踪法的优点在于制导系统结构较为简单，但缺点是所生成的飞行轨迹弯曲严重，所需过载大，对战机的空气动力、结构强度、制导系统等各方面提出了较高的要求;平行接近法的突出优点是战斗机的引导轨迹较为平直，但实现起来相当复杂;比例引导法的战斗机飞行轨迹比较平直，而且制导系统容易实现，实际引导系统中比较常用，可以作为远距引导的方法之一;另外还有一种以最优控制理论为基础的时间最优引导律，以其引导时间最短作为远距引导的引导律，下面介绍其引导原理。

2.3 时间最优引导原理

以图3所示的水平面引导过程为例。在远距引导阶段，要求战斗机全速追踪，即要求追踪时间最短，所以战斗机远距引导问题属于最优控制中末端时刻自由，末端状态约束的非线性最优问题［9-10］。引导时间是衡量指标，为了使引导总时间tf最短，就必须让其性能函数J达到最小。

性能函数为

引导律方程的一般形式为

由式(3)写出哈密尔顿函数为

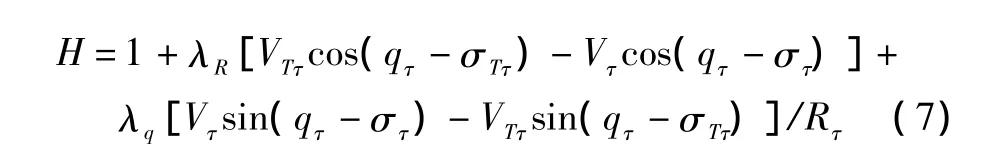
协态方程为

在t=tf时满足边界条件，又哈密顿函数为

由极值条件∂H/∂στ=0 得

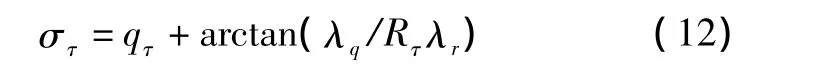
由式(4)～式(8)可得

式(13)说明战斗机的方向指向战斗机、目标的最后视线方向。

为了实现战斗机引导的最优时间控制，必须找到精确的qfτ值，要解式(1)的非线性微分方程是很困难的，但是对末端时刻t=tf，进行几何分析有［11］

首先，战斗机的运动方程为

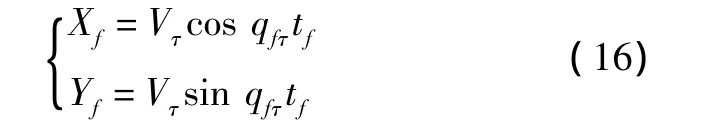
其次，假设目标的运动轨迹角σTτ是时间的已知函数，得t=tf时刻目标的位置为

本研究入选高龄冠心病患者行介入治疗和药物保守治疗后6个月内发生全因死亡、非致死性心肌梗死、心力衰竭、心绞痛发生情况，两组都未发生全因死亡事件发生，介入治疗组患者发生非致死性心肌梗死、心力衰竭、心绞痛发生率明显低于药物治疗组，有统计学意义。两组患者包括非致死性心肌梗死、心力衰竭、心绞痛、全因死亡在内的总事件发生率，介入组明显低于药物组。综上所述，对于高龄冠心病患者在进行治疗的过程中，为患者应用介入治疗方案进行治疗能够提高临床治疗的效果，而且治疗具有较好的安全性，值得推广应用。

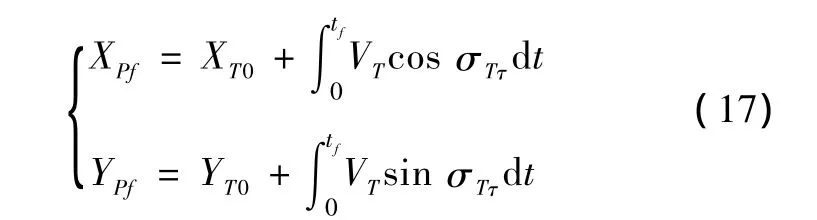
把式(16)、式(17)代入式(14)、式(15)可以解出qfτ，tf。式(14)转换为

应用Newton-Raphson二次收敛迭代求得一个近似的 tf值，并代入式(15)，则 qfτ被确定。

导出时间最优引导律(OPG)的控制指令为

离散形式为

同理，在垂直面内qfτ也可被确定。

采用时间最优引导律，战斗机远距的引导时间将达到最优，从而使远距引导效果达到最佳。

3 战斗机远距引导控制律

在远距引导阶段，要求战斗机全速追踪，即要求追踪时间最短［11-12］，所以基于远距引导阶段时间要求最小的考虑，本文在战斗机的远距引导阶段采用时间最优引导法来获得远距引导的快速性，满足了这个要求，也就达到了战斗机远距指挥引导的最优指标。根据前面提出的自动攻击的概念，必须将时间最优引导过程中战斗机的控制参数分离出来，即战斗机飞行速度V、战斗机飞行高度H、战斗机飞行航向ψ，把这些参数提供给战斗机飞行控制系统，战斗机就可以实现远距的自动攻击。

4 仿真实例

图5～图7分别是战斗机比例引导法和时间最优引导法的水平面轨迹图、垂直面轨迹图和三维轨迹图。

图5 战斗机远距引导水平面轨迹图Fig.5 Horizontal track of fighter plane and target

图5中，当战斗机与目标相距120km时，战斗机进入到能够通过自身雷达发现目标的空域，远距引导结束，战斗机被成功引导至指定空域。圆形区域是水平面内战斗机远距引导截止区。由水平面轨迹图可以看出时间最优引导法在引导的初始阶段用最大角速度转弯对准截获目标航向，引导轨迹较为平直，其在水平面的引导效果优于比例引导法。

图6、图7中，由于远距引导时，战斗机、目标在高度方向相对水平面距离变化不明显，按比例显示垂直面和三维轨迹图时，战斗机高度变化不明显，所以在绘制垂直面轨迹图和三维轨迹图时，横、纵坐标不采用等比例表现。从图6中可以看出垂直面内时间最优引导轨迹也较为平直。

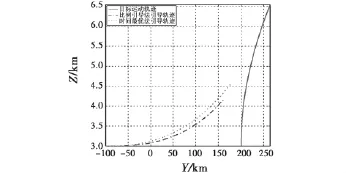
图6 战斗机远距引导垂直面轨迹图Fig.6 Vertical track of fighter plane and target

图7 战斗机远距引导三维轨迹图Fig.7 Three-dimensional track of fighter plane and target

图8是战斗机、目标比例引导法和时间最优引导高度变化图。

图8 战斗机远距引导高度变化图Fig.8 Altitude change of fighter plane

图9是战斗机比例引导法和时间最优引导法航向变化图，仿真中航向角以X轴正半轴为参考，逆时针变化时、航向增加，反之，航向减小。

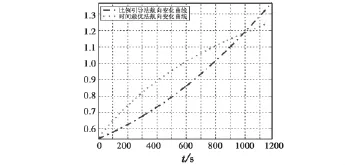
图9 战斗机远距引导航向变化图Fig.9 Course change of fighter plane

图8，图9中战斗机高度，航向变化以及战斗机速度(本例中为定值)可以作为远距引导时战斗机的飞控参数以实现自动攻击。

表1是比例引导法和时间最优引导法完成远距引导的时间，由表可知，时间最优引导法引导时间上优于比例引导法。这也是战斗机远距引导全速追踪，即追踪时间最短的最好体现。

表1 战斗机引导时间Table 1 Guidance time of fighter plane

由仿真结果可知:时间最优引导法在引导的初始阶段用最大角速度转弯对准截获目标航向，直接采用了航迹角作为控制变量，利用末端的几何关系得到战斗机和目标的末端视线角，用这个末端视线角与当前航迹角的变化率作为输入量来控制航向，在引导时间上和轨迹上优于比例引导法，实现了时间最优引导性能，更适合战斗机的远距引导。

5 结论

本文针对传统战斗机引导对飞行员本身素质要求较高，且操控任务繁重的缺点，采用时间最优引导法作为远距引导律来实现战斗机的远距引导。并将引导过程中战斗机的高度、速度、航向作为飞行控制参数，实现了战斗机远距引导的自动攻击。

［1］于雷，李言俊，欧建军.现代战斗机最佳导引算法研究［J］.航空学报，2006，27(2):9-22.

［2］周焘.战斗机人工势场及其在空战指挥引导中的应用［D］.西安:空军工程大学，2007.

［3］陈冰，蔡满意，朱凡.进入角约束下的攻击机空间远距引导研究［J］.电光与控制，2010，17(9):17-20.

［4］RYOO C K,CHO H,TAHK M J.Time to go weighted optimal guidance with impact angle constraints［J］.IEEE Transactions on control systems technology,2006,14(3):483-492.

［5］孙体忠，孙金标.空战战术双层决策模型设计［J］.电光与控制，2011，18(4):37-40.

［6］高浩，朱培申，高正红.高等飞行动力学［M］.北京:国防工业出版社，2004.

［7］吴文海.飞行综合控制系统［M］.北京:航空工业出版社，2005.

［8］丁全心.现代空战中的战术辅助决策技术［J］.电光与控制，2009，16(12):1-4.

［9］BECKER K.Closed-form solution of pure proportional navigation［J］.IEEE Transitions on Aerospace and Electronic Systems,1990,AES-26(3):526-532.

［10］MCFETRIDGE L M.IBRAHIM Y.New technique of mobile robot navigation using a hybrid adaptive fuzzy potential field approach［J］.Computers ＆ Industrial Engineering,1998(35):471-474.

［11］陈超.超视距多目标攻击及战斗机引导关键技术研究［D］.南京:南京航空航天大学，2006.

［12］周荻.寻的导弹新型引导规律［M］.北京:国防工业出版社，2002.