基于R阵动态估计的自适应滤波算法

苌永娜， 张 海， 李玉洁， 杨 静

(北京航空航天大学控制一体化技术国家级重点实验室，北京 100191)

0 引言

在观测噪声动态估计研究中，文献［1］提出了自适应更新状态噪声、观测噪声误差统计特性的方法;文献［2］提出了基于新息序列的自适应开窗逼近法，依据观测信息自适应调整状态协方差阵和观测协方差阵;文献［3］提出了一种动态自适应抗差滤波算法，能够自适应地分配观测信息和模型信息对状态估计的权重。

对于线性系统而言，上述观测噪声特性统计方法均依赖于新息量，如果一步状态预测值估计不准确，观测噪声特性的估计会出现偏差，从而影响滤波精度。

本文从组合导航系统中不同测量系统的测量互补特性出发，在一定情况下，通过相对测量关系的构建，实现观测噪声的动态估计，在此基础上，以预设滤波精度为指标，通过构造自适应因子对估计观测噪声进行适当的调节，最终实现高精度的自适应滤波。

1 基于R阵动态估计的自适应滤波算法理论分析

1.1 现有自适应滤波算法分析

标准卡尔曼滤波(SKF)中，状态估计和滤波增益为

自适应滤波是通过估计或修正系统模型参数、噪声特性或滤波增益等方法来提高滤波精度的，例如渐消滤波［4］和抗差自适应滤波［5-7］在SKF基础上的改进如下所述。

渐消滤波增益阵为

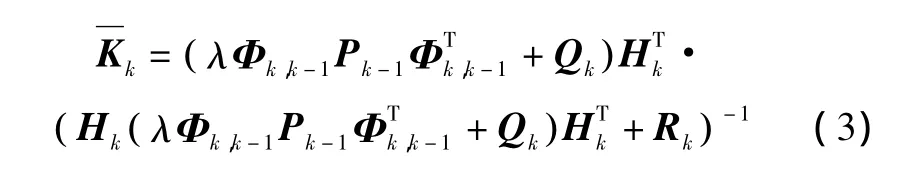
其中:Φk，k-1为系统一步转移矩阵;Qk为系统噪声方差阵;Pk-1为状态估计方差阵。

抗差自适应滤波增益阵为

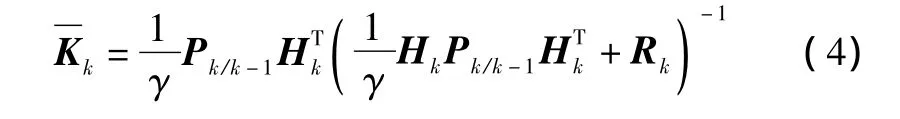
渐消因子λ与抗差自适应因子γ分别为

其中:tr［·］为矩阵求迹符号;c0为常值。

渐消滤波将验前状态协方差矩阵膨胀λ(λ≥1)倍，抗差自适应滤波通过构造自适应因子γ(0＜γ≤1)来调节状态噪声的协方差阵，由式(3)、式(4)看出，两者的最终结果均是将滤波增益阵K增大，从而提高观测信息的利用权重，但当观测误差变大时，其滤波效果将明显变差。由式(5)、式(6)知，λ与γ的构造均是新息量的函数，一旦状态估计值有较大误差，对观测噪声的估计会出现偏差，从而影响自适应滤波的估计精度和稳定性。

1.2 观测噪声R自适应估计方法分析

文献［8］针对GPS/DR系统提出了一种改进的航向估计算法，利用GPS和陀螺仪信息自适应估计航向测量噪声方差阵R。文献［9］提出了一种基于不同测量系统测量特性的观测噪声方差阵R自适应估计定理，并从理论上证明了其正确性。设对于同一物理量Z(k)同时存在两种不同的测量系统M1、M2，并且两系统的测量特性互补。其中，测量系统M1的测量结果在真值附近抖动，在某些情况下其抖动幅度较大，而M2具有短时高精度，且其测量值的变化趋势与真实值的变化趋势基本一致。设两系统测量值分别为Z1(k)、Z2(k)，单测量系统自差分序列分别为ΔZ1(k)、Z2(k)，且

则M1的测量噪声方差阵R可进行如下近似估计:

对于测量噪声方差阵R的估计，文献［9］中提出了一种连续滑动窗口的统计方法，在GPS/INS机载导航系统中进行了仿真验证，当测量噪声方差阵R满足在一定区间内近似为同分布的条件时，此方法能够获得良好的估计效果。但是，滑动窗口的宽度在实际应用中难以确定，并且若窗口内只有当前历元的观测误差很大，由于使用了大量历史数据的平滑作用，会使当前历元观测噪声的估计值降低，从而无法获得当前历元状态量的最优估计。此外，此方法也在一定程度上增加了计算量和存贮量。

1.3 基于R阵动态估计的自适应滤波算法

在实际系统中，观测噪声的动态特性通常是复杂多变的，为如实反映各个历元瞬时噪声特性，本算法基于R自适应估计定理的思想，针对单次历元的观测噪声特性进行动态估计。事实上，基于不同测量特性的R估值定理可以获得接近实际系统的测量噪声特性(文献［9］已进行了仿真验证)，但若直接作用于滤波解算中，滤波效果并不十分理想。

在卡尔曼滤波中，式(3)第二项体现了修正信息对状态估计的贡献，其权重由Kk确定。对于观测信息Zk，基于双测量系统的R估计定理主要针对观测噪声的随机误差进行估计，并未考虑系统误差;对于Hk，由于设计卡尔曼滤波器时选取的系统模型往往包含一定的不确定性，因此也包含了一定的误差，从而造成修正信息可信度的下降。Kk是建立在P和R均可精确获得的理想情况下的最优增益，而这在实际系统中难以实现。因此为减小状态估计误差，本文从预设的定位精度ε出发，在当前滤波增益阵Kk的基础上乘一个自适应因子α(0＜α≤1)，等价于将估计R进行一定程度的膨胀作用(设为β倍，β≥1)，将系统误差、模型误差的影响包含进来，从而得到精度更高的滤波估计。

由于状态向量通常含有不同类型的参数，且各观测分量对同一状态量的作用也不尽相同，因此本文采用序贯处理方法对各观测分量进行处理。设Rk为对角阵(在实际系统中具有一定的普遍性)，主对角线元素，…，k均为一维变量。依据序贯处理思想，设k时刻，对于第i个观测分量，有

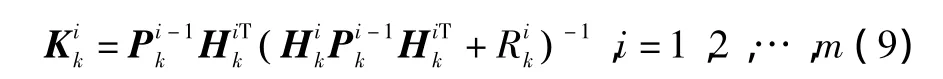
定义自适应因子为α=diag［α1α2… αm］，相应地 β=diag［β1β2… βm］。

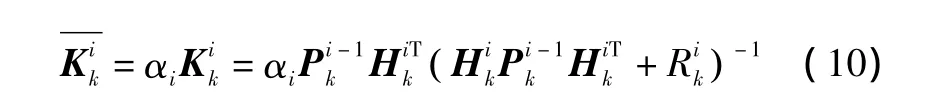
因此新的滤波增益阵也可以表示为

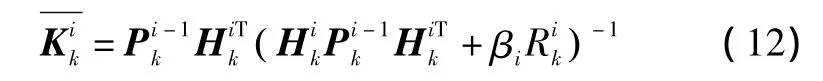
由式(12)及式(14)联立可得

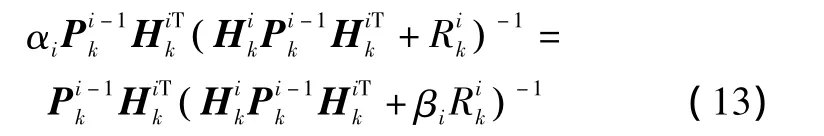
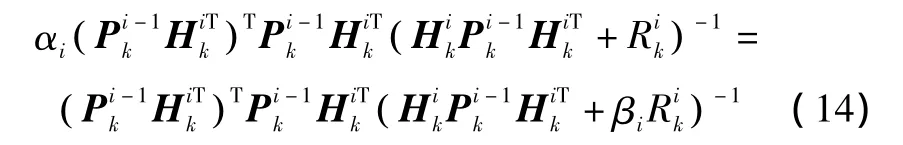
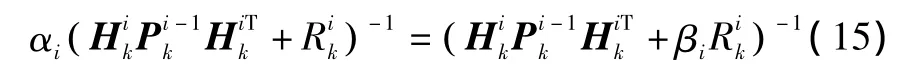
因αi不为零，式(15)两边分别求逆，得

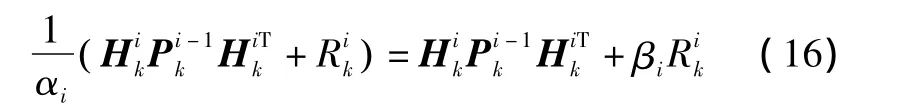
由于0＜αi≤1，最终新的噪声阵为

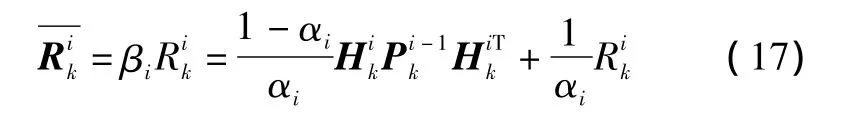
2 基于R阵动态估计的自适应滤波算法实现

1)单测量系统自差分。

设k时刻，如第1.2节所述，组合导航系统中两测量系统的测量值分别为Z1(k)、Z2(k)，首先对两测量系统分别求单系统自差分序列ΔZ1(k)、ΔZ2(k)为

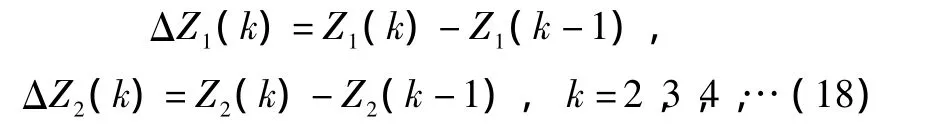
2)双测量系统互差分。

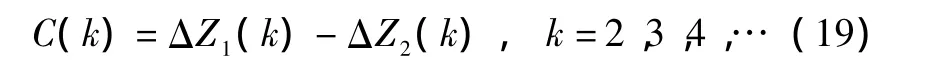
3)双测量系统互差分序列单历元估计。

4)自适应因子的构造。

设组合系统需要达到的定位精度为ε，测量噪声估计分量值为R^ik，基于测量噪声估计方差阵映射的观测误差水平，自适应因子αi可构造为

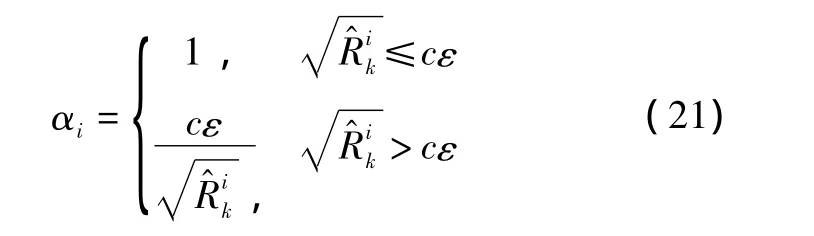
其中，c为常数，通常取为0.2 ～0.8。

5)本自适应滤波的序贯处理核心算法。

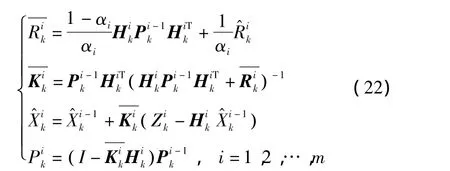
同SKF相比，本自适应算法仅增加了各历元双系统互差分及自适应因子的简单计算，并且采用序贯处理方法，对Zk各分量进行顺序处理，将对高阶矩阵的求逆转变为低阶矩阵的求逆，有效降低了计算量。

3 算法验证

3.1 GPS/DR组合导航滤波模型

为验证本算法的有效性，本算例在GPS/DR实际系统中，在多遮挡、多障碍物的路段，对机车进行高精度定位。本文采取直接法建模，选取的状态向量为，各分量依次为北、东向位置，航向角，速度，航向角速度，陀螺仪零偏B，里程仪刻度因子S;选取的观测向量为Z=，各分量依次为 GPS测量的北、东向位置、航向，里程仪测量的速度，陀螺仪测量的航向角速度。

本文采用EKF方法进行线性化，得出的状态转移矩阵Φk+1，k及观测矩阵Hk如下:

其中:T为滤波周期;Pod为里程仪测量的脉冲数。

3.2 算例分析

3.2.1 实验条件

机车运行初始条件:位置为北纬36.598090°、东经114.451120°，航向角为 322.0755°，速度为 2.7344 m/s。GPS采用差分定位，为实现高精度定位，本实验中将经纬度坐标转换为WGS-84直角坐标系。本实验中，机车在钢厂的铁轨上运行，相邻铁轨大约为5 m，并且由于工况要求，机车运行速度较低，主要对东、北向位置进行估计，定位精度要求为5 m。

3.2.2 对比算法

除标准卡尔曼滤波以外，本算法与改进的sage-husa自适应算法［9］及 MAKF［10］算法进行了同条件对比实验。改进的sage-husa自适应算法只针对观测噪声R的统计特性进行自适应估计。MAKF算法中，GPS测量噪声的估计方法为

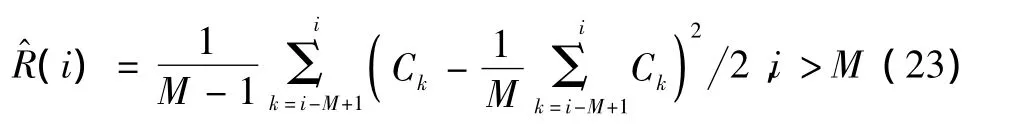
其中:i为当前滤波时刻;Ck为双系统互差分序列;M为滑动窗口宽度，此处取为30。

3.2.3 仿真结果分析

在实验条件下，GPS测量结果如图1所示。150～174 s、230～245 s区段内GPS信号良好，定位结果正常;175～229 s区段内GPS由于受到周围高层建筑物的影响，输出结果明显偏离真实轨道。采用SKF、改进的sage-husa算法、MAKF算法及本自适应算法进行GPS/DR组合导航滤波解算，实验结果如图2及图3所示。其中本算法构造自适应因子时，经过反复试验，式(21)中常数c最终取为0.2。与其他各算法相比，本算法能够自适应地跟踪周围环境的变化，输出结果光滑连续，最大定位误差为4 m，满足预设精度要求。

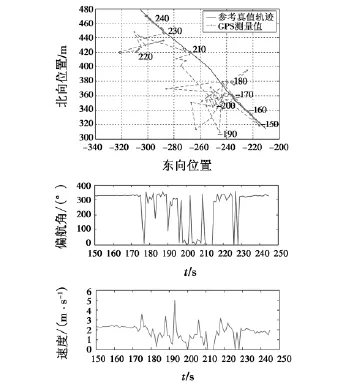
图1 GPS测量结果Fig.1 The output of GPS

从图2a、图2c中可以看出，SKF中观测噪声的统计特性由验前统计结果获得，其结果恒定不变(10 m2)，其他算法可对观测噪声进行自适应估计。175～198 s时间段内，GPS的噪声特性实际上已经发生了较大变化，但是改进的sage-husa算法、MAKF算法均未做出响应;200～230 s时间段内，在GPS的定位误差较大的情况下，虽然改进的sage-husa算法、MAKF算法对GPS的噪声特性进行了自适应估计，但估计动态性能较差;231～245 s时间段内，GPS已恢复正常定位，而改进的sage-husa算法、MAKF算法对GPS观测噪声的估计仍严重偏高;整个时间段内，本自适应滤波算法快速、及时地跟踪了GPS噪声特性的变化。

由于改进的sage-husa算法在对R更新时耦合了状态估计误差的影响，因而估计结果不可靠。MAKF算法对R的估计建立在窗口内各历元的统计结果的基础上，因而会受到历史数据平滑作用的影响，削弱了对观测噪声估计的动态性能，从而使其在高动态的实际系统中的应用受到限制。本自适应算法针对单次历元的观测噪声特性进行估计，避免受到大量过去数据的影响，且在对R的估计过程中不存在与状态估计误差协方差阵P的耦合关系;从预设滤波精度出发，基于估计的观测噪声水平确定自适应调节因子的比例，对当前估计观测噪声信息进行适当的膨胀作用，相当于将观测估计误差、状态估计误差等包含进来，从而实现了准确、可靠的滤波估计效果。

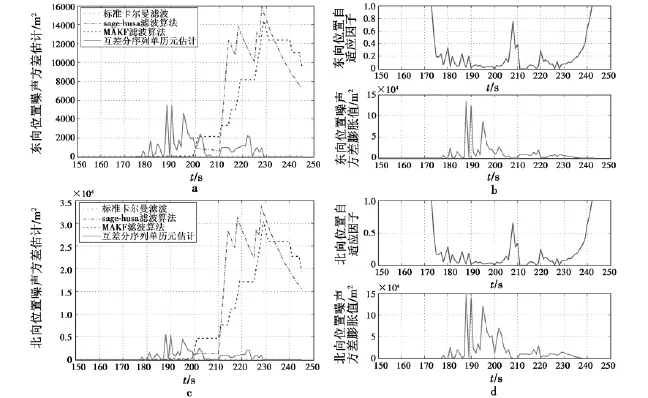
图2 4种算法的R估计结果Fig.2 Comparison of four Kalman filtering algorithms in estimating R

图3 4种算法实验结果对比Fig.3 Comparison of four Kalman filtering algorithms

4 结论

本算法基于组合导航系统中不同测量系统的测量特性，构造相对测量关系估计单次历元的噪声特性，避免了现有估计方法中状态误差和历史数据的影响;在满足预设精度的前提下，通过构造自适应因子对估计R阵适当调节，收敛于滤波增益K阵对观测信息有效利用的准则，有效地提高了滤波精度。同改进的sage-husa算法、MAKF等现有自适应滤波方法相比，本自适应算法在实际系统中得到了良好的应用，在滤波精度和抗干扰性能上，具有明显的优越性，具有深入的理论推广意义和工程实用价值。此外，由于组合导航系统中通常存在某些两个测量系统及以上的物理量，因此本文主要针对双测量系统的测量特性进行自适应估计，对于只有单个测量系统的物理量，可以考虑构造等效观测量的方法进行估计，值得进一步研究。

［1］SAGE A P,HUSA G W.Adaptive filtering with unknown prior statistic［C］//Proceedings of Joint Automatic Control Conference，Washington DC:American Automatic Control Council,1969:760-769.

［2］MEHRA R K.On the identification of variances and Adaptive Kalman filtering［J］.IEEE Transactionson Automatic Control,1970,15(2):175-184.

［3］CUI X，YANG Y.Adaptively robust filtering with classified adaptive factors［J］.Progress in Natural Science,2006,16(8):846-851.

［4］王虎，王解先，白贵霞，等.改进的渐消卡尔曼在GPS动态定位中的应用［J］.同济大学学报，2011，39(1):124-128.

［5］YANG Yuanxi,GAO Weiguang.Comparison of two fading filters and adaptively robust filter［J］.Geo-spatial Information Science,2007,10(3):200-203.

［6］YANG Y,GAO W.An optimal adaptive Kalman filter［J］.Journal of Geodesy,2006,80(4):177-183.

［7］YANG Yuanxi,GAO Weiguang.A new learning statistic for adaptive filter based on predicted residual［J］.Progress in Natural Science,2006,16(8):833-837.

［8］刘倩，张海，周艳丽，等.改进的GPS/DR组合导航自适应航向估计算法［J］.电光与控制，2010，17(6):71-77.

［9］张海，常艳红，车欢.基于GPS/INS不同测量特性的自适应卡尔曼滤波算法［J］.中国惯性技术学报，2010，18(6):331-336.

［10］常艳红.GPS/INS组合导航自适应滤波技术研究［D］.北京:北京航空航天大学，2010.

［11］WANG Jian,LIU Jiang,CAI Bogen.Study on information fusion algorithm in embedded integrated navigation system［C］//2008 International Conference on Intelligent Computation Technology and Automation,2008:1007-1010.