无人机紧密编队协同控制设计与仿真
陈春东, 魏瑞轩, 董 志, 张立鹏, 钮 磊
(1.空军工程大学航空航天工程学院,西安 710038;2.中国人民解放军驻沈阳飞机工业集团有限公司军事代表室,沈阳 110850;3.中国人民解放军94590部队,山东潍坊 261000)
0 引言
无人机编队协同可以提高执行任务的成功率和抗突发事件的能力,在侦察、干扰以及对地攻击等方面具有单机无法比拟的优势。特别是无人机紧密编队飞行,更可以极大地节省动力需求,提高航行距离、飞行速度和负载重量等能力。无人机紧密编队协同控制研究引起了国内外学者的广泛关注[1]。
紧密编队协同控制主要解决的问题是飞机之间相对位置的保持和空气动力的影响。目前,对于编队飞行控制问题的研究,文献[2]提出使用内外环控制的思想;文献[3]使用常规的PID设计方法进行设计;文献[4]采用反馈线性化的设计思想。总结这些设计方法,主要是以编队动力学模型为设计基础,采用相应的设计思路,能够达到良好的控制效果,但研究对象均为非紧密编队,编队的数学模型忽略了无人机间的气动耦合效应,不能用于无人机紧密编队的控制设计。文献[5]使用直接自适应控制技术和混合PID控制器设计了编队飞行控制系统,仿真结果表明设计的编队飞行控制系统达到了理想的效果,但研究的只是二维环境下的无人机质点模型编队飞行控制问题;文献[6]分析了紧密编队的气动耦合影响,但文中并未涉及到控制器设计问题。
本文在上述研究的基础上,以两架无人机紧密编队为研究对象,首先,从力学角度分析两架无人机之间的气动耦合影响,得出僚机气动力和力矩的变化;其次,分析僚机的动力学和运动学特性,建立僚机相对于长机的三维编队控制数学模型,在此基础上,进行控制器的设计;最后,对设计的控制系统进行了仿真验证。
1 紧密编队的动力学分析
无人机紧密编队飞行是指两机之间的侧向距离不大于一个翼展的编队,这样长机所产生的翼尖涡就会对其跟随僚机的飞行动力性能产生很大的影响[7],这种紧密编队飞行时存在的耦合效应将使僚机的气动力及力矩发生变化,此种情况下,气动耦合及相对运动诱发的耦合将影响无人机紧密编队动态模型。
1.1 上洗和侧洗模型
如图1所示,两机在紧密编队飞行时,长机两翼面将产生涡流,两翼处产生的涡流具有很强的聚合趋势,因而翼面所产生的所有涡流在脱离翼面后,靠近翼尖的某个位置处会汇合成左右两条大的涡流带,左右两条涡流带具有大小相同,方向相反的涡强。

图1 涡流带形成示意图Fig.1 Sketch map of vortex
研究表明[6]两条涡流带的距离(等效翼展)如图1所示,其中b为无人机翼展。僚机在长机产生的涡流带飞行时,会受到上洗诱导速度和下洗诱导速度的作用,从而使自身的空气动力和力矩发生改变。因为涡流带为无限长,所以暂不考虑沿涡流带方向的影响。
本文采用20世纪初NASA的Burnham提出的马蹄形模型来描述涡流带。诱导切向速度为
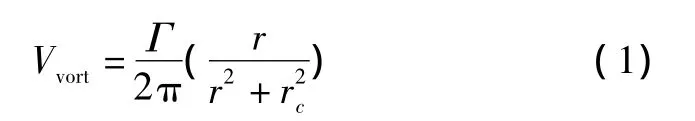
式中:Γ为涡强;r为测试点到涡线的距离;rc为涡核半径,通过引入有限长涡核半径来克服经典模型存在接近涡线时有奇异点的问题,同时利用涡核半径将涡流衰减效应模型化,研究表明[8]涡核半径会随着时间的增加而不断增长。
根据式(1),计算诱导速度的关键在于距离r和涡强Γ的计算,其中距离r的计算,如图2所示,有位置几何关系
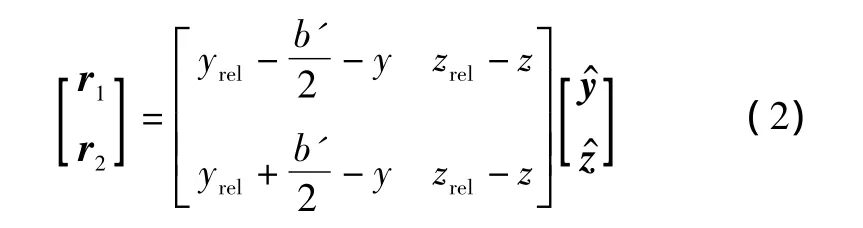
式中:r1、r2分别为长机上僚机相对长机的左翼和右翼的距离矢量;yrel、zrel分别为长机和僚机的侧向相对距离和相对高度;y^、z^分别为图示方向单位矢量。

图2 长机僚机位置几何关系图Fig.2 Geometry position of the lead and wing planes
涡线环量可以根据Kutta-Joukowski定理来获得,表达式为

式中:AR为展弦比;V为飞机速度;CL为升力系数;b为翼展。
将式(2)和式(3)带入式(1),得僚机上某点(y,z)受到上洗速度W和侧洗速度V。
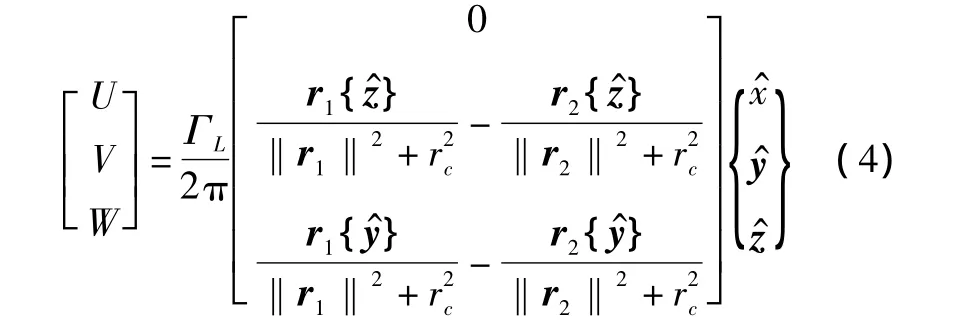
式中:‖·‖表示向量的模;ri{j^}表示向量ri在j方向上的分量;U为沿流束方向的诱导速度,如前所述,其值为零。
1.2 气动耦合下空气动力的变化
忽略无人机纵向运动和横向运动的铰链影响,因而纵向力和垂直力、俯仰力矩仅受上洗速度的影响,横向力、偏航力矩仅受侧洗速度的影响,滚转力矩同时由上洗速度和侧洗速度决定。因为本文建立的是无人机三自由度模型,所以对无人机的气动力矩不做讨论,下面分析无人机的阻力、升力和侧力的变化。
机翼上洗引起机翼迎角变化,它使得升力合力矢量发生转动。设V∞为飞机速度,W为上洗速度,则迎角变化为故升力变化量为其中,Lα为升力曲线斜率。这里假设Δα很小,升力矢量转动引起阻力的变化为
由于涡流带在僚机的两翼翼面各处均会产生升力和阻力,因此采用积分的方法求僚机在长机涡流带影响下的升力变化和阻力变化(下标W,L分别表示为僚机与长机)。表达式为
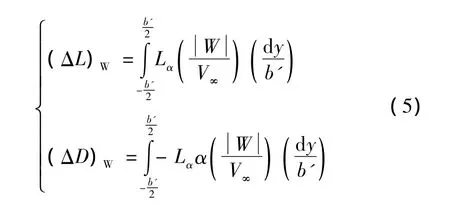
将式(4)代入,得到僚机在长机涡流带影响下空气动力变化为
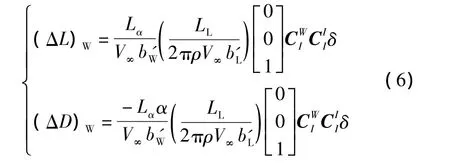
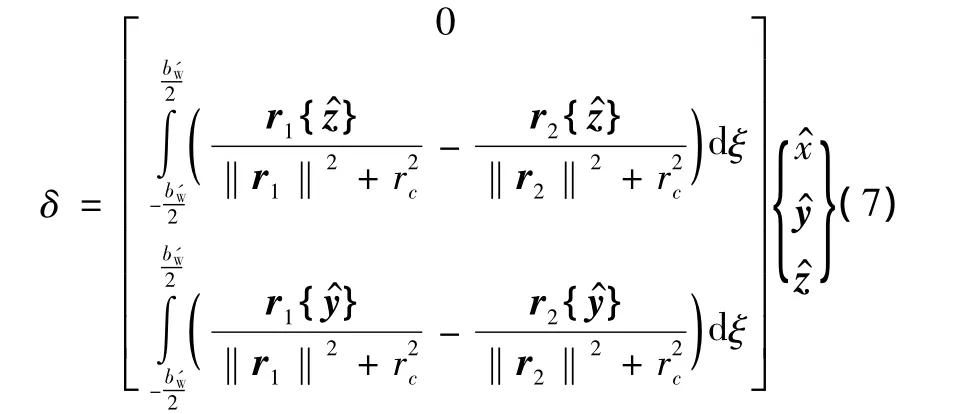
同理,根据飞行力学知识,侧力Y的变化为
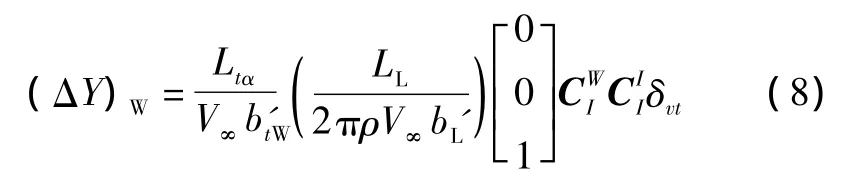
式中:Ltα为垂尾的升力曲线斜率;btW'为僚机的等效垂尾长度,无因次表达式δvt为
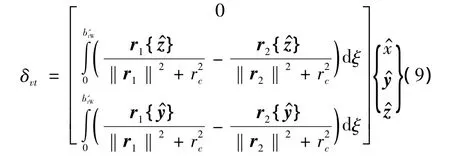
2 紧密编队的数学模型
数学模型的准确性和合理性是设计良好控制系统的关键所在,在进行了紧密编队时的动力学分析,得到僚机力的变化的基础上,建立无人机紧密编队的数学模型。其中下标W表示僚机,下标L表示长机。
首先,在惯性坐标系下建立僚机的动力学模型

式中:γW、φW、ψW为僚机坐标系相对于惯性坐标系的欧拉变换角,分别为航迹倾斜角、滚转角和偏航角;LW、TD、YW为僚机所受到的力,分别是升力、阻力和侧力;TW为僚机发动机可用推力;mW为僚机质量;VW为僚机速度。
其次,根据图3所示,长机和僚机的相对位置关系,建立僚机相对于长机的运动学模型。
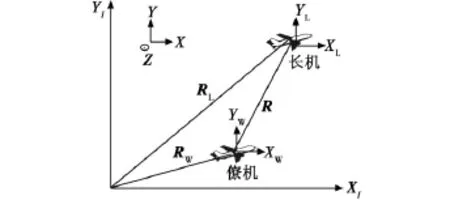
图3 长机僚机的相对位置关系示意图Fig.3 Sketch map of the lead and wing planes'position
由位置矢量关系
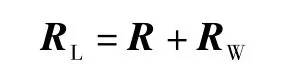
两边矢量求导,得

由式(10)知僚机角速度矢量ωW为
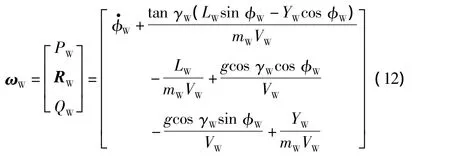
将式(11)代入式(12),得无人机编队运动学模型为
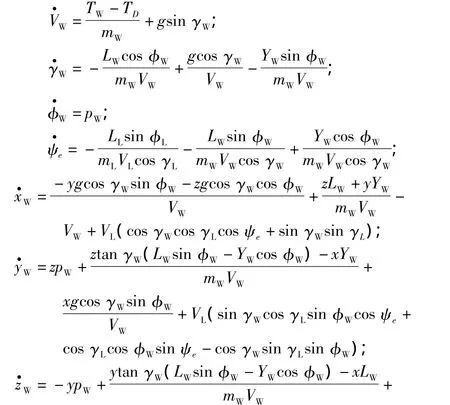

上述编队模型状态变量 X=[VW,γW,φW,ψe,xW,yW,zW],因不考虑力矩的影响,所以无人机的控制输入变量U=[TW,LW,pW]。另外,建立此编队模型的主要目的是为了设计僚机的编队控制器,因此,可以认为,长机的参数 ζ =[VL,γL,LLsin φL]为设计控制器时的干扰向量。需要说明的一点是,在上述导出的模型中,凡是僚机的空气动力都是气动耦合引起的力的变化值和僚机本身的气动力的合成。
3 紧密编队飞行控制系统设计
3.1 控制系统结构
本文建立的编队模型为非线性模型,针对无人机编队运动的非线性模型发展了许多控制方法,如文献[9]采用PID算法设计控制器;文献[10]采用 Slide Model控制算法来实现编队的形成和保持。另外还有基于视觉的编队控制算法[11]以及其他算法等[12]。
但是目前几乎所有进行编队飞行实体试验的控制器均采用PID设计,这是因为其他算法在工程上实现起来相对比较困难。而PID控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好、工程实现方便以及可靠性高等特点,尤其适用于可建立精确数学模型的确定性控制系统,被广泛应用于过程控制和运动控制中。因此,结合工程应用性,本节根据PID控制的设计原理以及在编队控制器设计中的应用,结合上节所建立的编队控制数学模型,采用经典PID方法设计编队控制器。
对于两架无人机,编队飞行控制就是在恒定的速度下,保持飞机之间的相对位置不发生变化。那么必须知道长机的基本姿态和位置,本文采用比例-积分-微分(PID)的控制结构,首先设计长机的PID控制器,然后以长机为参考模型,根据上面建立的紧密编队数学模型。设计僚机的编队控制器,使其跟踪长机的状态,实现紧密编队的稳定飞行。
3.2 控制器设计
在编队飞行控制系统中,长机按照常规的PID控制器设计方法设计航迹和马赫数保持控制回路,其具体控制律为
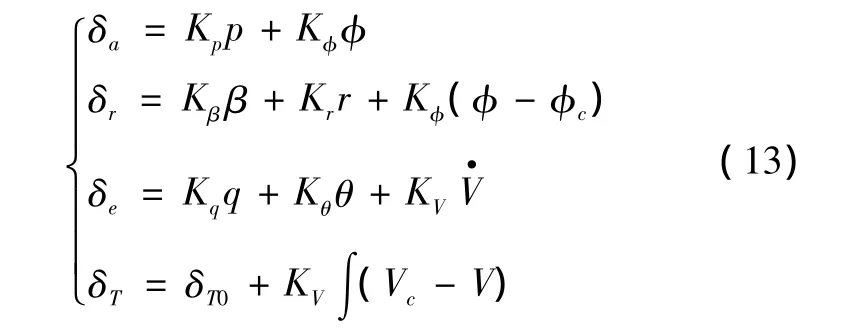
式中:δa、δr、δe、δT分别表示副翼、方向舵、升降舵和推力的控制量;K 表示相应的控制参数;φ、β、θ、p、q、r分别表示滚转、侧滑、俯仰角,以及滚转、俯仰、偏航角速率。
设计僚机控制器时,假设所需的长机信息完成能够得到。因为紧密编队时,存在气动耦合效应,所以在设计编队控制器时,区别一般的控制器设计,准确考虑气动耦合的影响是设计的关键。
X通道控制器的设计采用常规的PID控制。Y通道控制滚转角速率,考虑与侧向运动有关的动力学特性时需要加入分离误差的二阶导数和航向角偏差的比例反馈。Z通道控制器的设计,根据文献[5]研究结论:紧密编队引进的气动耦合项使无人机的Y耦合进了Z通道。因此,在设计Z通道控制器时应考虑Y通道的气动耦合效应。
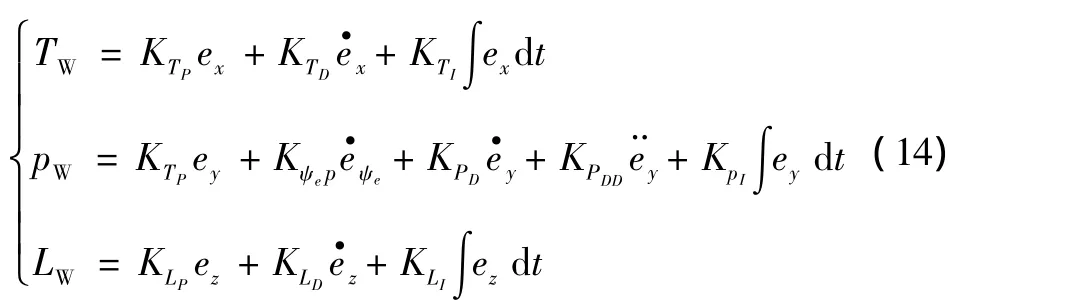
式中:K为相应的控制参数,误差信号定义为
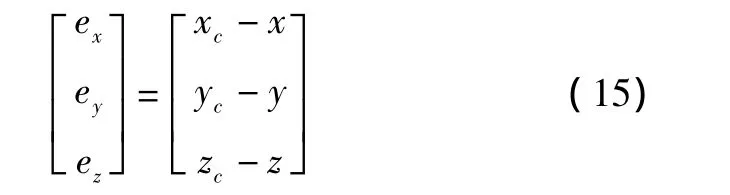
控制器中,比例环节成比例地反映控制系统的偏差信号,偏差一旦产生,控制器立即产生控制作用,以减少偏差。积分环节主要用于提高编队控制的精度,提高编队控制的无差度。微分环节反映偏差信号的变化速率,并在编队误差信号变得太大之前,在编队控制中引入一个有效的早期修正信号,从而加快编队控制的动作速度,减少调节时间。另外,因为编队控制数学模型中长僚机相对位置的数学表达式存在耦合,所以误差信号也存在耦合,虽然从控制器设计的形式中不能看出,但实际上设计时,已经充分考虑了这点。
4 仿真分析
应用两架无人机在高度为4500 m,Ma=0.5的飞行状态下进行仿真。仿真时间为60 s,采样周期为0.05 s。长机的初始化参数偏航角和速度分别设定为0 rad和150 m/s,设置长机和僚机相对位置的期望值为(25 m,8 m,0 m)。
如图4所示,为设定在两机相对位置为(28 m,10 m,1 m)的初始条件下,通过编队控制器的作用,两机相对位置误差逐渐减小。由图可知,在20 s以后趋于稳定,编队误差趋近于零。图4中右侧分别为相应各通道的控制律变化曲线。
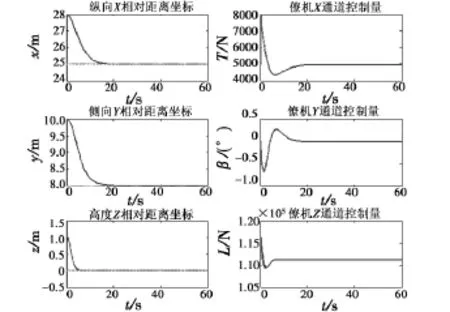
图4 紧密编队相对位置和相应控制输入图Fig.4 Curve of close formation and control input
图5为当长机分别以加速度a=0.25 m/s2加速和减速40 s时,僚机速度跟踪变化曲线。

图5 紧密编队速度变化跟踪图Fig.5 Curve of speed follow in close formation
图6为两机编队飞行的三维空间航迹,由图可知,长机空间机动的过程中,僚机迅速形成了期望队形,并能准确跟踪队形控制指令,在飞行中保持队形的稳定。
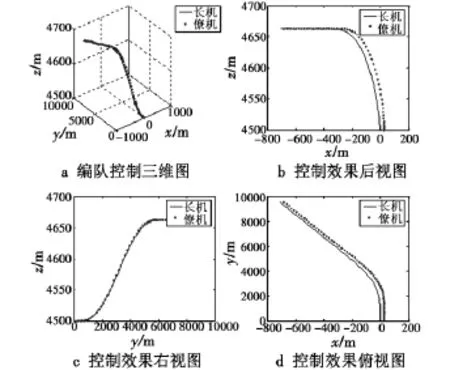
图6 紧密编队三维空间航迹仿真图Fig.6 3D simulation of flight path in close formation
从仿真结果可以看出,本文提出的编队飞行控制方法充分利用了两机之间的状态特性,僚机实现了对长机的良好跟踪。总结算法,得出下述结论:
1)编队飞行控制解决的是在复杂环境下的协调控制问题,将长机和僚机的控制律分开设计,使得问题简化;
2)本文应用飞行力学的知识建立了紧密编队的非线性数学模型,采用经典的PID控制方法设计了编队控制器,使得设计的系统结构简单明确,适合于工程应用;
3)本文只是研究了无人机编队控制的三自由度数学模型,在后续的研究中将对六自由度模型的编队飞行控制进行深入研究。
5 结论
本文以两架紧密编队的无人机为研究对象,从飞行力学角度分析紧密编队的空气动力耦合影响,分析僚机的动力学和运动学特性,建立了三维编队控制数学模型。考虑到气动耦合的影响和编队飞行实体试验的工程控制方法,采用经典PID方法设计了紧密编队控制系统。仿真结果表明本文设计的紧密编队飞行控制系统具有较强的鲁棒性和自适应跟踪能力,能够较好地实现无人机编队空间机动条件下编队形成与保持,并且具有编队形成速度快、编队误差小的优点,达到了理想的效果。本文设计的算法运算简单,适合于工程应用,为解决复杂无人机编队系统的飞行控制设计拓宽了研究思路。
[1]樊琼剑,杨忠,方挺,等.多无人机协同编队飞行控制的研究现状[J].航空学报,2009,30(4):683-691.
[2]GIULIETTI F,INNOCENTI M,NAPOLITANO M,et al.Dynamic and control issues of formation flight[J].Aerospace Science and Technology(S0034-1223),2005,36(9):65-71.
[3]ZUO B,HU Yun’an.UAV tight formation flight modeling and autopilot designing[C]//Proceedings of the 5th world congress on Intelligent control and Automation,Hangzhou,June 15-19,2004,USA:IEEE,2004:180-183.
[4]SEMSAR E.Adaptive formation control of UAVs in the presence of unknown vortex forces and leader commands[C]//Proceedings of the 2006 American Control Conference Minneapolis,Minnesota,USA,June 14-16,2006,USA:IEEE,2006:3563-3569.
[5]刘小雄,张卫国,王振华,等.无人机自适应编队飞行控制设计与仿真[J].系统仿真学报,2009,21(5):1420-1422.
[6]柳勇,吴密翠.密集编队气动耦合效应分析[J].飞行力学,2001,19(2):12-16.
[7]MCGILL S.Compound aircraft transport study:Wingtip-docking compared to formation flight[C]//The 41st Aerospace Sciences Meeting and Exhibit,Reno,Nevada,AIAA,2003:315-320.
[8]VENKATARAMANAN S,DOGAN A.Modeling of aerodynamic coupling between aircraft in close proximities[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit,Providence,Rhode Island,AIAA,2004:941-945.
[9]RYAN K,OSTEROOS B S.Full capability formation flight control[D].Captain:Air Force Institute of Technology Air University,2005.
[10]GALZI D,SHTESSE Y.UAV Formations control using high order sliding modes[C]//Proceedings of 2006 American Control Conference,Minneapolis,2006:4249-4254.
[11]CRUM V,HOMAN D,BORTNER R.Certification challenges for autonomous flight control systems[R].AIAA,2004:52-57.
[12]XIE Feng,ZHANG Ximing,FIERRO R.Autopilot based nonlinear UAV formation controller with extremum seeking[C]//Proceedings of the 44th IEEE Conference on Decision and Control,and the European Control Conference,Seville,Spain,2005:4933-4938.

