基于偏差流的多工位装配顺序优化研究
石 炜,宋政立,王建国,张文兴
(内蒙古科技大学 机械工程学院,包头 014010)
0 引言
偏差流建模理论主要有:基于几何运动学偏差分析,如极值法,蒙特卡洛法等,该类模型难以应用到复杂的零件装配过程;基于有限元的偏差分析,如Liu提出的一维偏置梁单元模型和力学偏差仿真模型[1]、GM公司Hsieh的偏差优化模型[2]等,该类模型主要着眼于两零部件的偏差协调分析,不能从装配全过程角度描述偏差传递,难以体现偏差的传递和过程分配中的错综复杂关系;基于统计模型的偏差分析,如加拿大Wateloo大学的Lawless和Mackay等[3]的一阶自回归模型,该类模型是事后处理,依赖大量数据训练学习;基于状态方程的偏差分析,Jin和Shi[4]提出的状态空间模型,该模型是基于机理的建模,能够反映偏差在多工位间以流动的形式积累、耦合最终形成产品的过程,能够应用到复杂的多工位装配过程。
应用偏差流状态空间模型可以对多工位装配过程仿真,预测偏差。状态空间模型的可观性分析可以应用于偏差源诊断和测点布置等研究[5];状态空间模型的可控性分析可以应用于夹具优化设计和公差综合等研究[5]。在偏差流状态空间模型基础上,提出装配顺序矩阵,实现对过程信息的数学矩阵化处理,建立多工位装配参数化状态空间模型。以装配顺序矩阵和状态空间模型为工具,优化装配路线,降低产品尺寸偏差,提高产品质量。
1 多工位装配偏差流状态空间模型
多工位装配过程包含大量的过程工艺信息,它们对最终产品质量影响巨大。提炼过程工艺信息,建立基于偏差流的状态空间模型,可以对多工位装配过程进行仿真并预测产品尺寸偏差。
多工位装配过程是指产品由多个零件经过多个工位装配而成,如图1所示的装配过程共有N个工位,在工位k,前k-1个工位上形成的零件称为总成件,新零件与总成件装配在一起形成工位k+1的总成件。依此类推最终形成产品。在工位k,零件偏差不但与本工位有关,而且与之前k-1个工位累积偏差有关。偏差在工位间累积、耦合,最终形成产品的偏差状态。偏差主要来源于4个方面:1)当前工位的夹具定位偏差,如图1中Uk;2)前序工位的累积偏差,如图1中Xk-1;3)更换夹具引起的重定位误差;4)装配中的噪声干扰,如图 1 中 Wk。
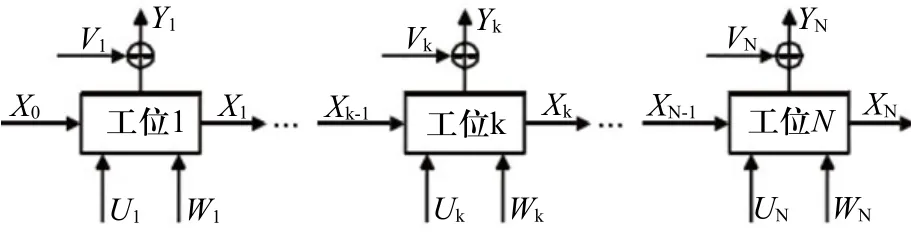
图1 多工位装配过程流程图
多工位装配过程相当于线性时变多输入多输出的离散系统,其状态空间模型[6,7]为:
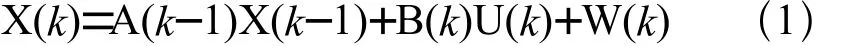

式(1)是状态方程,式(2)是输出方程,其中k是工位序号,A是n×n矩阵,n为状态变量个数,称为系统矩阵,反映前序工位累积偏差和重定位偏差对本工位偏差状态的影响;B是n×m矩阵,m为输入变量个数,称为输入矩阵,反映当前工位夹具定位偏差对本工位偏差状态的影响;C是r×n矩阵,r为输出变量个数,称为输出矩阵,反映零件上测点和参考点的相对关系。当前工位不进行测量时,C(k)为零矩阵;W,V为装配和测量过程中的噪声干扰。
将状态空间模型式(1),式(2)合并,忽略零件装配前的偏差,可得:
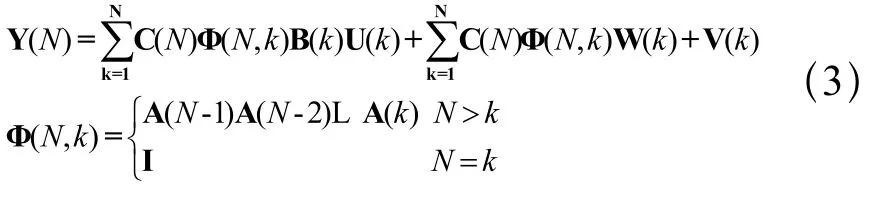
式(3)中Y(N)矩阵形式为:

式(4)可以简写成:
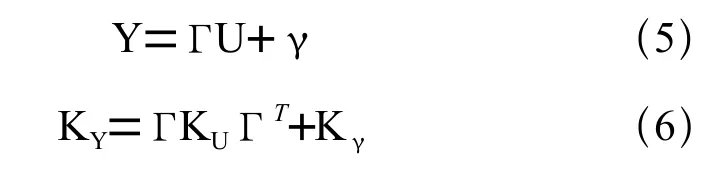
式(5)中U是输入变量,Γ是模型矩阵,γ为装配和测量时的噪声干扰总和。对式(5)等号两边取协方差计算,得到式(6)。式(5)、式(6)即为多工位装配过程状态空间模型矩阵表达和方差形式。
2 装配顺序矩阵
多工位装配过程包含大量的工艺信息,在建模之前需要将这些工艺信息(如零件数、工位数、装配顺序、定位销布局、被重定位的零件等)提炼出来;在设计装配路线阶段,需要对不同的装配路线进行仿真,这就意味着大量工夹具的更换,即工艺信息的改变。装配顺序矩阵可以满足频繁改变工艺参数的需求,快速地提炼过程工艺信息。
装配顺序矩阵,即order矩阵形式如下:
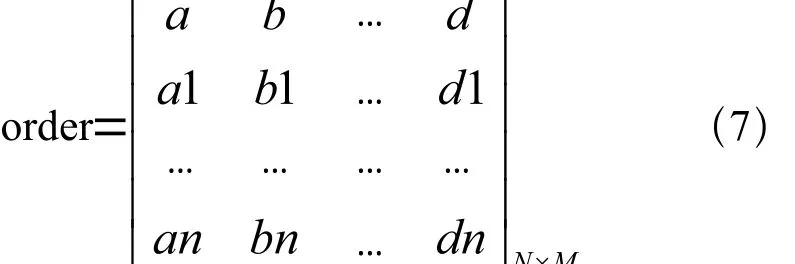
order矩阵有N行,代表装配过程共有N个工位,每行元素代表该工位定位销布局。每行前两个元素代表总成件上定位销布局,决定哪些零件被重定位。后面的元素代表待装配零件的定位销布局,决定零件装配顺序。没有新零件装配到总成件时用零元素代替,在编程建模时,使用continue语句结束当前工位的装配操作。零件装配顺序矩阵可以确定零件总数和当前工位总成件的构成。
如图2所示是典型的多工位装配过程案例,其过程工艺参数可以由其装配顺序矩阵,即式(8)确定。式(8)中order矩阵有三行,确定装配过程有3个工位。第一行元素有4个非零元素,说明在工位1两个零件装配形成总成件。第二行有6个非零元素,说明在工位2总成件与两个新零件完成装配。第三行只有前两个元素非零,说明只有总成件被定位,工位3是测量工位。由每行奇数列的非零元素[13;157;1],可知零件装配顺序是零件1→零件2→零件3,4。由每行的前两个元素[12;14;18],可知在工位2,零件1,2被重定位,在工位3零件1,4被重定位。


图2 典型的多工位装配过程案例
此外在设计装配路线阶段,改变order矩阵的元素就能达到改变装配路线的目的。完成图2产品的装配,装配顺序矩阵还可以是:

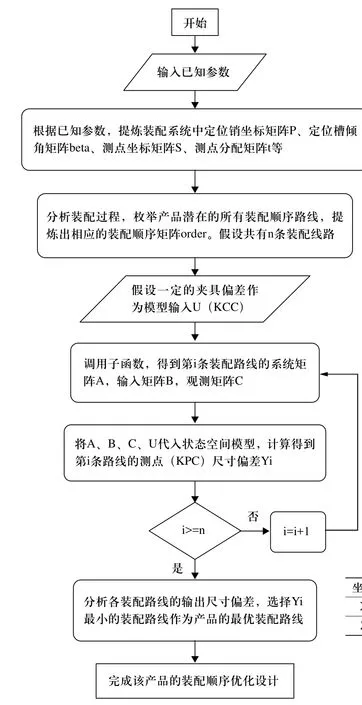
图3 优化装配路线流程图
式(9)代表另外三条装配路线,即路线1:零件2→零件3→零件4→零件1;路线2:零件2→零件3→零件1→零件4;路线3:零件2→零件3,4→零件1。
装配顺序矩阵能够实现对多工位装配过程工艺信息的数学矩阵化处理,工艺信息的改变只要通过改变装配顺序矩阵的元素就能够实现,调用order矩阵,利用循环语句可以快速构建状态空间模型,对多条装配路线仿真,预测偏差,完成装配路线的最优设计。
利用状态空间模型和装配顺序矩阵优化具体产品的装配路线,具体过程如图3所示,优化的装配顺序能够减少输入偏差(KCC偏差)对输出偏差(KPC偏差)的影响,使得装配系统更稳健,产品尺寸偏差越小,质量越高。
3 实验分析
以某轿车车身侧围装配过程为例构建偏差流状态空间模型,预测零件尺寸偏差,实现工艺路线的最优选择。侧围简图如图4所示,装配过程包括4个零件,即零件1—A柱、零件2—B柱、零件3—侧顶、零件4—侧板。这些零件为结构件,具有较大的刚度,定位采用3-2-1定位方式[8](一面两销定位和夹紧),零件通过焊接的方式连接到一起,满足建模假设条件。按照图3所示流程完成该产品的装配路线优化设计。
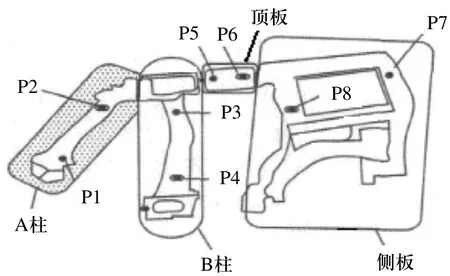
图4 产品最终装配效果图

表1 定位销P的坐标(单位:mm)

表2 测点S的坐标(单位:mm)
各零件上定位销P(奇数点为四向定位销,偶数点位两向定位销)和测点S坐标如表1,2所示。在设计装配路线阶段,拟定4套装配路线,即:
路线1:零件1→零件2→零件3→零件4;
路线2:零件2→零件3→零件4→零件1;
路线3:零件2→零件3→零件1→零件4;
路线4:零件3→零件4→零件2→零件1。
上述四条工艺路线对应的装配顺序矩阵分别是:
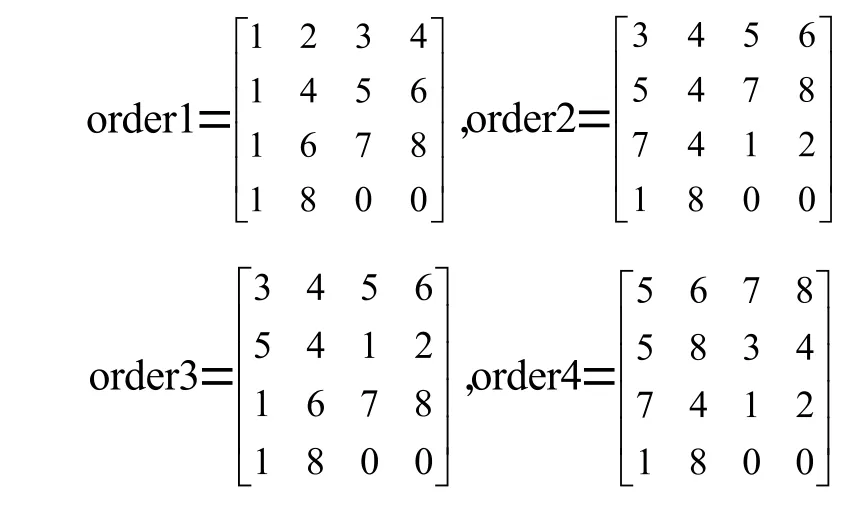
对于具体装配路线各工位定位销的选择可以有很多种,本文采用最大距离原则选取定位销定位,即选择几何距离最大的定位销组定位。
根据已知条件和order矩阵,利用Matlab软件编程构建偏差流状态空间模型,由于篇幅限制,不再给出各装配路线的系统矩阵A、输入矩阵B、观测矩阵C的具体形式,只给出第一条装配路线Γ矩阵的具体形式,如下:
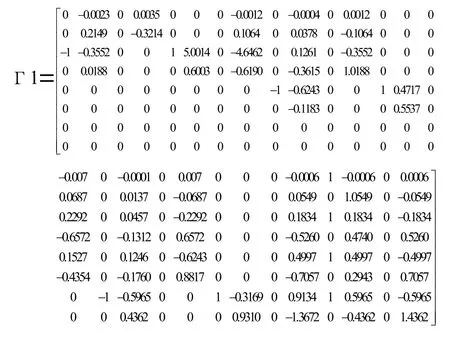
假设所有定位销的定位偏差为±1mm,根据±3δ原则,定位偏差U∈N(0,1/6)。在Matlab中生成服从N(0,1/6)分布的随机数组作为状态空间模型的输入向量,忽略噪声项,应用式(5)进行100次仿真,最终预测各测点尺寸偏差如表3所示。
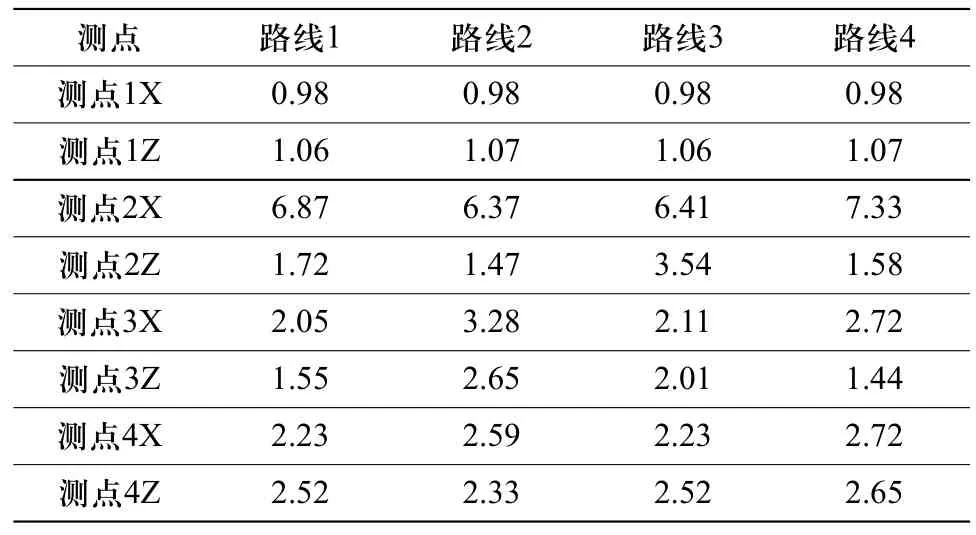
表3 测点尺寸偏差预测值(单位:mm)
由表3可知,四条装配线路在测点1的预测中差异微小,不能单从测点1出发判断装配路线的优劣。路线1与路线2相比,在测点3和4处,尺寸偏差较小且与路线2差距明显,路线1优于路线2;路线2与路线3相比,在测点3和4处,尺寸偏差略大,但在测点2处,尺寸偏差显著的小于路线3,可知路线2优于路线3;路线4与路线2相比,在测点3处尺寸偏差显著小于路线2,但在测点2上尺寸偏差显著大于路线2,可知路线2和路线4优劣性相当,路线4略优于路线2。根据优劣性排序,路线1>路线4>=路线2>路线3。选择路线1作为产品的装配方案。
4 结论
提出基于偏差流状态空间模型的多工位装配顺序矩阵,即order矩阵,实现对具体装配工艺路线和过程工艺信息的数学矩阵化处理。在order矩阵的基础上,利用循环语句在Matlab中建立参数化偏差流状态空间模型,能够对多工位装配过程仿真,预测产品尺寸偏差,实现装配路线最优设计。该模型为后续的偏差源诊断、夹具优化、测点优化等工作提供了数学基础。
[1] Liu S, Hu S J.Variation simulation for deformable sheet metal assemblies using finite element methods[J].ASME Journal of Manufacturing Science and Engineering, 1997,119: 368-374.
[2] Hsieh C, Kong P.Simulation and optimization of assembly processes involving flexible parts[J].Journal of Vehicle Design, 1997, 18(5): 455-465.
[3] Lawless J F, Machay R J, Robinson J A.Analysis of ariation transmission in manufacturing processes–part I[J].Journal of Quality Technology, 1999, 31(2): 131-142.
[4] Jin J, Shi J.State space modeling of sheet metal assembly for dimensional control[J].ASME Journal of Manufacturing Science and Engineering, 1999, 121(4):756-762.
[5] 田兆青.轿车车身装配偏差流的状态空间建模方法及应用基础研究[D].上海, 上海交通大学机械与动力工程学院, 2008.
[6] 文泽军, 刘德顺, 杨书仪.多工位装配过程夹具系统公差和维护综合优化设计[J].机械工程学报, 2009, 45(12):151-161.
[7] 田兆青, 来新民, 林忠钦.多工位薄板装配偏差流传递的状态空间模型[J].机械工程学报, 2007, 43(2): 202-209.
[8] CAI Wayne.Robust pin layout design for sheet-panel locating[J].International Journal of Advanced Manufacture Technology, 2006, 28(3): 486-494.

