基于PSO-SVM的3SPS+1PS并联髋关节试验机正运动学研究

成钰龙，程 刚，顾 伟，山显雷

（中国矿业大学 机电工程学院，徐州 221116）

0 引言

评价人工髋关节材料需进行摩擦学试验。目前国内外髋关节试验机运动平台均采用串联模块，在复杂运动轨迹模拟和变载荷动力加载等方面尚存在不足。相对于串联机构，并联机构精度高、速度快、刚度大、承载强且累计误差小[1]，目前已在运动模拟器[2]等方面得到了成熟的运用。本文以3SPS+1PS并联机构为核心运动模块搭建了一台髋关节摩擦磨损试验样机，模拟人体髋关节运动规律。正运动学分析是该试验机正常工作的前提，求解并联机构正运动学的方法有：解析法、附加传感器法、数值法和神经网络法。其中人工神经网络法在求解并联机构正运动学上受到了广泛的关注，但其存在一些固有缺陷如收敛速度慢、局部最小值和通用性差等，故需研究更有效的正运动学求解法。

支持向量机作为处理分类和回归问题的有效工具，基于结构风险最小化原则，具有通用性强、解的稀疏表示等优点。本文采用粒子群优化过的支持向量机回归法对3SPS+1PS并联髋关节试验机正运动学进行求解。分析结果显示，PSO-SVM能有效解决机构正运动学问题。

1 运动学建模

常用机构空间位姿描述方法有四元素法和Rodrigues参数法等。四元素法综合性能较高，但仍有一定约束条件。根据ISO14242-1:2002(E)标准，人工髋关节假体在进行摩擦学实验时，试验机的运动频率为1Hz±0.1Hz[3]，对求解方法的速度要求较高。Rodrigues参数实现了四元素向三维独立参数的转化，不涉及三角函数运算，较大程度地减轻了实时姿态解算的计算量。用Rodrigues参数表示的姿态旋转矩阵为D[4]。

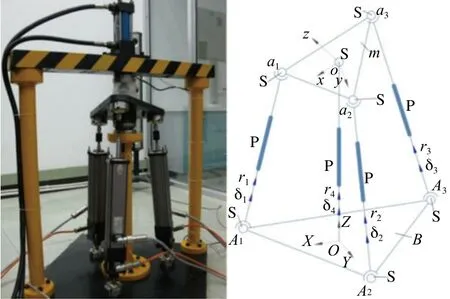
图1 3SPS+1PS并联髋关节试验机样机及其拓扑图

该试验机由定、动两平台组成。三条主动支链连接两平台，中心支柱支撑动平台。图1为髋关节试验机样机及3SPS+1PS并联机构拓扑图。建立参考坐标系如图1所示。定平台B连接点Ai(i=1, 2,3)、动平台m连接点ai (i=1, 2, 3)以及动坐标系原点O的位置坐标和oB表达式如下：

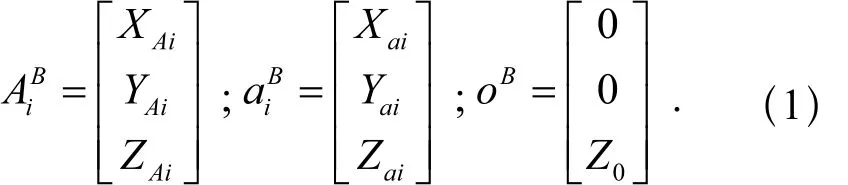
其中e是点ai到动平台坐标系原点O的距离，E是Ai到定平台坐标原点O的距离。(xl,xm,xn,yl,ym,yn,zl,zm,zn)是动平台m在{B}中的9个方位参数，构成描述动平台m位姿变换的旋转矩阵D。

由空间两点间距离公式可得支链ri(i=1,2,3)的长度表达式如下：

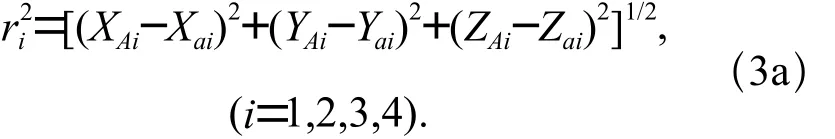
将式(1)、式(2)代入式(3a)可得各支链长度ri(i=1, 2, 3, 4)如下：

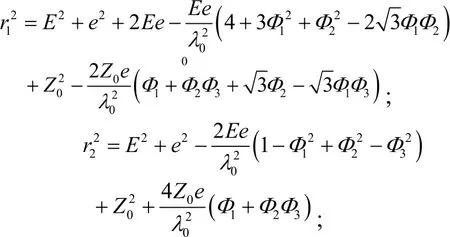
当给定支链的长度ri(i=1,2,3,4)和Zo的值时，动平台正位姿参数Φi(i=1,2,3)可通过以下过程进行求解，从而确定动平台在空间的姿态。

由式（3b）可得：

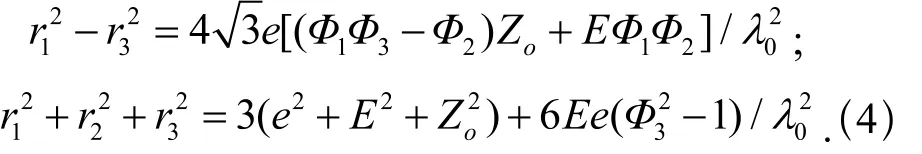
由式（3b）和（4），结合给定的支链长度值ri(i=1,2,3,4)和Zo值，通过求解非线性方程组可解得三个Rodrigues参数Φi(i=1,2,3)。

2 PSO- SVM正运动学求解算法

2.1 SVM简介

设训练样本集{(x1, y1) , (x2, y2) , … , ( xm, ym)}，其中xiRm,表示样本的输入空间，其对应的目标值 yiR, (i=1,2,…,m)。支持向量机回归方法的目的是建立一个超平面来精确逼近输入数据与输出数据之间的非线性映射，然后通过黑箱方法构造最优线性回归函数。

常用支持向量机回归估计函数为：f (x)=(wФ(x))高维特征空间的非线性映射函数[5]。

支持向量机估计的优劣通过损失函数和ε-不敏感损失函数来度量，其基本形式为：

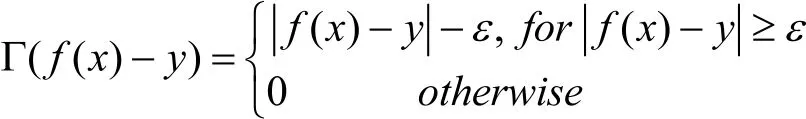
2.2 PSO算法对SVM参数的优化

支持向量机回归预测性能的优劣主要受惩罚参数c和核函数参数g的影响。对参数c、g最优解的选取目前尚无统一标准。粒子群优化算法(PSO)是基于群体智能的优化算法，它通过粒子在解空间追随最优粒子进行搜索。PSO算法收敛速度快、通用性强，一般情况下可很快收敛于全局最优解。本文将交叉验证意义下的预测均方误差作为PSO算法的适应度函数，通过PSO算法对SVM参数进行优化，利用所求得的全局最优解进行SVM网络训练。

2.3 基于PSO-SVM的正运动学求解过程

PSO-SVM求解正运动学的算法过程如下：

1）将逆运动学求解所得10000组解的前9000组作为训练数据集，后1000组作为测试数据集；

2）对训练数据集和测试数据集进行[0,1]区间归一化；

3）用归一化后的训练数据集作为SVM训练样本，通过PSO算法对SVM参数c和g进行全局寻优；

4）SVM采用全局最优参数c、g，以训练数据集作为学习样本进行训练，建立正运动学求解模型；

5）用测试数据集对建立好的正运动学求解模型进行测试；

6）评价测试结果。

3 仿真研究

采用PSO优化的支持向量机如图1所示并联髋关节试验机进行正运动学求解。该髋关节试验机结构参数见表1。

表1 3SPS+1PS 并联机构结构参数

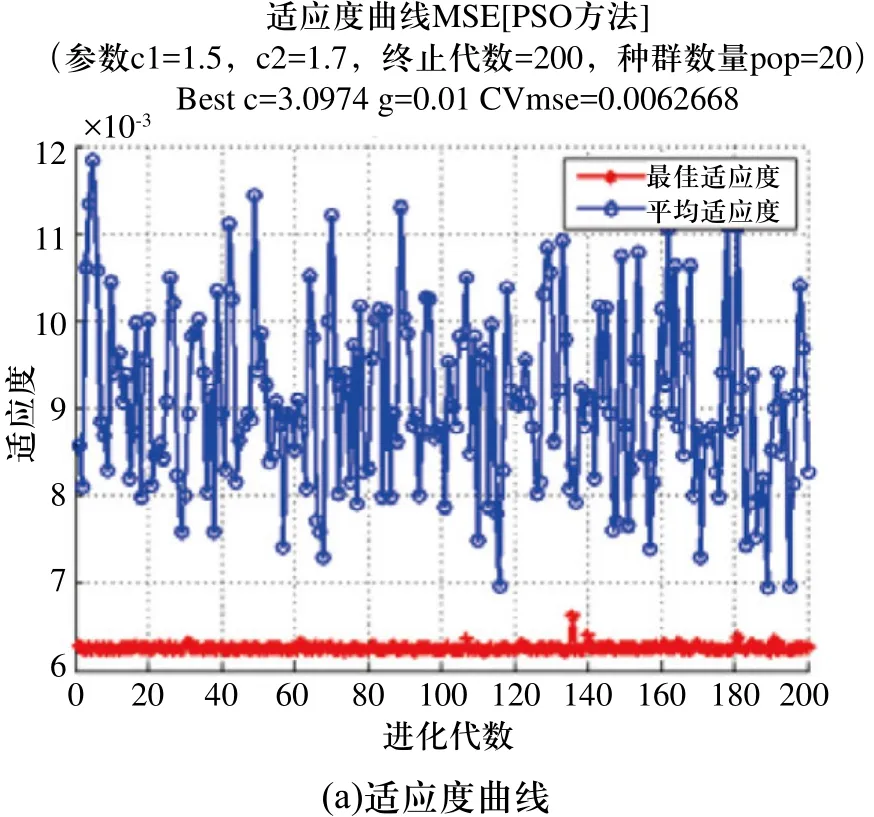
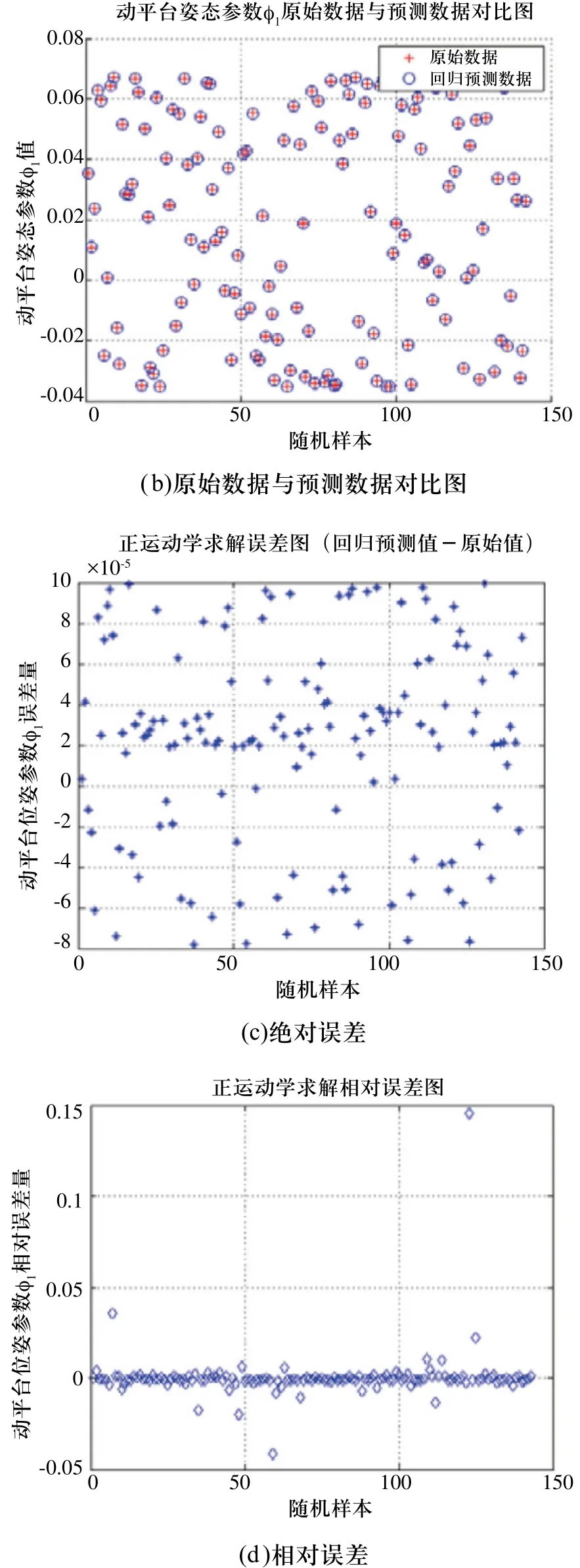
图2 PSO-SVM正运动学求解结果分析

该髋关节试验机在工作时需模拟人体髋关节的相对运动曲线，经过试验机逆运动学求解，得到1150组逆运动学解。随机选取1000组作为该正运动学求解的训练样本，另外150组作为测试样本。比较发现，具有线性核函数的ν-支持向量机在求解并联机构正运动学时性能优良。采用PSO算法优化过的ν-支持向量机分别对测试样本中的三个姿态参数Φi(i=1,2,3)进行预测。以参数Φ1的预测为例，其预测结果分析如图2所示。由图2可得粒子群算法优化后支持向量机CV意义下的全局最优参数c=3.0974，g=0.01。预测值与理论值最大绝对误差数量级为10-5个单位，最大相对误差为0.15，绝大部分相对误差在±1%之间。预测结果的均方误差为2.18167×10-7，相关系数为99.9998%，满足并联机构正运动学求解精度要求。

为了衡量本文利用PSO对SVM参数优化的有效性，本文采用传统SVM作为对比模型，对比求解结果如表2所示。

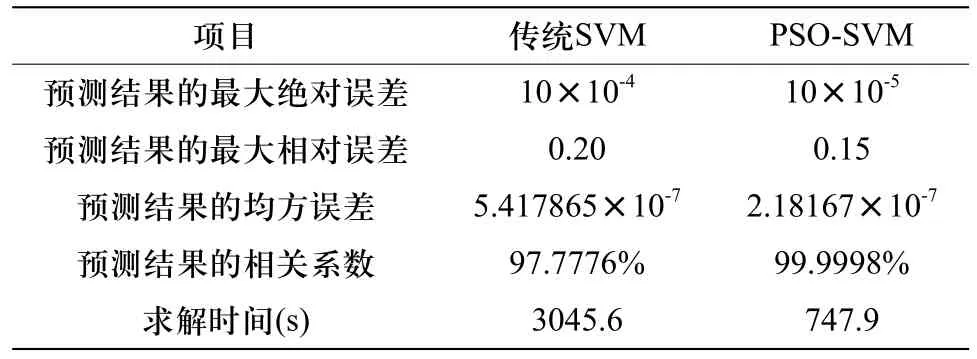
表2 传统SVM与PSO-SVM正运动学求解结果对比

从表2可知，PSO-SVM并联机构正运动学求解算法精度远高于传统SVM算法，但运算时间相对较长。结果表明通过PSO算法优化获得SVM参数是全局最优的。

4 结束语

针对人体髋关节的实际生物特性，研制了一台3SPS+1PS并联髋关节试验机。基于Rodrigues参数对3SPS+1PS并联髋关节试验机进行运动学建模。应用PSO算法优化过的ν-支持向量机对该试验机的正运动学进行求解，求解精度满足机构控制精度要求。通过与传统SVM支持向量机正运动学求解进行对比分析，证明PSO-SVM具有较高精度。

[1] Olazagoitia JL, Wyatt S.New PKM Tricept T9000 and its application to fl exible manufacturing at aerospace industry.SAE International, Paper No.07ATC-94, 2007.

[2] Chun-TaChen, Jyh-Chyang Renn, Zong-Yuan Yan.Experimental identif i cation of inertial and friction parameters for electrohydraulic motion simulators, Mechatronics 2011(21)1–10.

[3] ISO 14242-1:2002(E).Implants for surgery-Wear of total hipjoint prostheses-Part 1: Loading and displacement parameters for wear-testing machines and corresponding environmental conditions for test.

[4] 周江华, 苗育红, 王明海.姿态运动的Rodrigues参数描述[J].宇航学报, 2004, 25(5): 514-519.

[5] Zhang Dan, Le Jian-he.Kinematic analysis of a novel 3-DOF actuation redundant parallel manipulator using artif i cial intelligence approach.Robotics and Computer-Integrated Manufacturing 2011(27)157–163.