再论真正常识否定5千年“常识”:没最大自然数——数学课本极重大根本错误:将两异集误为同一集

黄小宁

(hxn268@126.com 广东 广州 510631)

丁肇中:“99%的人反对你，不代表他们是对的。专家的评论是依靠现有的认识，而科学的发现是推翻现有的认识。”（2011.10.17《新华每日电讯》2版）。钱学森希望大学能培养出有科学发现才能的杰出人才。应试教育摧残人的智力与学力，“高分低能”就远谈不上能有科学发现。发现的方法是“渔”。“科学”共识:初等数学绝不会有重大根本错误。“反科学”的太“反动”发现来自于太浅显逻辑学常识:①若R+各元x（相比下）全都是≈0的极小正数则R+绝不可含全部正数而必有正数>>R+所有数x；②…；…。故可如小学生看图识字那样看图识本文的发现。本文突出特点:是否真的推翻了5千年都没人能推翻的科学“常识”当然事关极其重大，但凡懂“一一对应”概念的中学教师等都有能力评判本文的正确与否性而非只有极少数人才能评判。

1 “一对一”常识让{n}的末项一下子暴露出来——对无穷数列的认识一直存在极重大缺陷与错误

设有圆形房门的旅馆空房间○序列○○...，给各○都挂上非0门牌号数得“夫妻”序列P:①②③...就用光已知非0自然数全体N的一切数n了，即N各数（或各号牌）与各○已一一配对。现又建一○，给其配挂数1就须摘下原①中的1，...——对各○重新编号（即数与○重新配对）的整个过程中始终都总有一○不能配有N的数表明全部○多于N的全部数（全部号牌）。注！为保证重新编号的号数都∈N(不可有N外数与○配对)不可涂改门牌号的数字且号牌背面不可有数。例要将房2改称是房1只能改变门牌号的位置:将原①中的1摘下改挂到原房2——须老老实实地按此 “没一摘就没一挂”的“死板”原则重新配对而不能没改配偶而只是改配偶的“名字”（例将n号房的号牌上的数n涂改为2n得②④⑥...——百年假象:部分号牌就可挂满P全部房间）。毛泽东:“要过细，粗枝大叶不行，粗枝大叶往往搞错。”老眼昏花的某人嫌女儿的对象张三穷而强令她改与李四处对象，她坚决不从但又不能硬顶，于是就换名不换人地让张三改名为李四；女父先入为主地坚信“我女绝不敢骗我”，故未戴眼镜粗枝大叶地看了几眼就将此新李四误为前李四了。同样…。

规定一数只能挂在一空房○内或外。P中1退出房间得P′:○②③...中的○没P′的数与之配对，除非拆散某对 “夫妻”。看图可知一n前移到空房○内的同时n号房就变空成○且在n的后面，这是一对一的:“拆东补西”地让一数前移到空房内的同时又生一新空房在前移数的后面。故 “各非1数n≥2都改与n-1号房配对”的重新配对法则令各n都前移一格到空房○内得②③④...中必有一○在各数的后面，因“拆东补西”前后的空房是一样多的，显然此○是P′的末项。故N有最大元t（若N是非0自然数全体则t是…）——推翻集论立论的论据:N各元n都有对应n+1、2n∈N。下节还要严格证明t的存在性。科学慧眼能洞察P′所有成员的配对情况而不被目光太短浅的肉眼所骗，不被“拆东补西”术迷惑。详论见[1]。故有革命结论:一给定无穷数列增（减）1个项后必比原来多 （少）1个项，{n≥1}不一定是N而有可能是其真子（扩）集。“推翻”此结论的症结:没有“过细地做工作”。

有傻瓜相机也有傻瓜数学:说y=2n>n中的n可取3、2、1就是说y可>这3个数，说n可遍取N一切数就是说y必可>N一切数而取N外数（后文指出N只是非0自然数全体的沧海一粟）。问题是不少人为了分数而扼杀自己的正常思维能力。故N各元n都有对应n+1、2n、…，但这所有对应数并非都∈N。故定义域为N的y=n＋1（或2n）的值域并非N的一部分！故中学“{n}必无末项”等等是重大错误。详论见[1]。两数之间有无穷多个数是常见的，例1与2之间的实数就多得写不完。有穷集Y的任何两元之间都绝不能有无穷多个Y的元——此性质不能硬套在无穷集W上，在W内必有一元与另一元相隔无穷多个W的元——此独特性质决定了无穷数列{n}中必有与首项相隔无穷多个项的项。

P中奇数都退出房间得○②○④○..中各数2n都左移到n号房内得②④⑥…；○○..——前列是“夫妻”列，后列是空房列，只不过各○都在一切夫妻的后面而肉眼不可见罢了。原因是有多少个奇数移出房就空出多少间房，而“拆东补西”前后的空房是一样多的。可见对无穷序列的认识一直存在…。引进思维“望远镜”使后列一下子暴露出来犹如医学有了电子显微镜使…。

2 再证{n}有末项推翻百年集论与百年“R完备”论

P={①②③..}中各“单人板凳”○与各数 n 已一一配对即n↔n号凳，将n看成是n号球员即“n=n号人”，①就是表示球员1坐在1号凳上的示意图，…，所有球员组成N。各n都改穿2n号球衣而改称是2n号人得②④⑥..——假象:部分球员可坐满P的○。文[1]有定理:

h定理1（重新配对定理）:有无穷多对“夫妻”的任一无穷有序数偶集中的“男、女人”之间任意重新配对（有的人“夺”别人配偶而“娶新欢”使有的人变成“单身”，一单身“再婚”就或使一与其异性的单身不再单身，或产生一与其同性的新单身，没别的可能。）后，一方出多少个单身，对方也必出多少个单身。

证:看图识理:P中任一n被n′夺去凳来坐的同时n′的原坐凳也变空了，这是一对一的，故每产一对新“夫妻”必同时产一对可配对的单身，这就使无论怎样的重新配对 （使P中人:有的变成“单身”后又“再婚”，继而又“单身”，继而又…，如此交替地进行；有的变单身后就一直单身而不再坐了；等等。）后有多少个人在凳外就同时出多少张空凳。关键是不可“混”入P外成员进行新配对。这说明定理成立。证毕。

设D～（对等于）D表示两D的元已一一配对:x↔x。两不交且非空的集 d、f的并记为 d＋f=H，d=H-f。G=N～N 中的 G 的非1元x=n＋1都被令改有新配偶n∈N（所有n=1，2，…组成U）后，G的 1（原有配偶 1∈N）就成单身，据 h定理1N也必出一单身t∉U显然是N的最大元！故“G各元x都可改有新配偶x＋1∈N”等等是不可实现的，否定此事实的症结:将N外数误为∈N，正如历史上人们曾力图将纳入有理数集抵制推翻“有理数完备”论一样。

图1内有两N且两N的元x与（x）一一配对成一数偶集在框框内，下N各元x的头上都有一（x）=x与其配成一对“夫妻”。下N的2改与其左斜上方的⑴∈上N配对，1与⑵就成一对单身；接着3改与斜上方的单身⑵配对就又产生一对含1 的新单身 1 与⑶；接着 4 改与单身⑶配对就..；…；x=n＋1 改与（x）=（n）配对就…——每产一对新夫妻必同时产一对（可配对）含1的新单身，故看图知下N的非1元x=n＋1都改有新配偶（n）∈上N的整个过程中1始终都总可有一单身∈上N与之配对。

图1

h定理2:任何无穷集W的任何真子集w都不可～W。

证 2（证 1 见[1]）:用反证法，假设 w′=w～W=w＋f成立则据h定理1在双方的元一一配对后再令w′=w各元x′=x都改有新配偶 x∈w=w′～w 后，w′（=w～w）方有 0 个单身的同时 W=w＋f方也只有0个单身，然而事实上f?W各元都是单身。故假设不成立。证毕。

定义:集 A与B的元 x与y:若可一一对应就称 A～B,若可一一对应相等就称A＝B。显然在未证明x与y可一一对应相等之前是不能断定A＝B的。

有大小的两圆形质点（圆心是点的中心）处在同一位置时它们的距离ρ是0，但它们相切时ρ=？规定两橡皮点之间的距离是它们的中心的连线的长。一截橡皮筋（橡皮点集）拉长后各点都变长了使点与点间的距离也变大了（例两端点的距离变大了），但各点的前后顺序关系没变。这是一种有序集的元的保序增距变换，其逆变换是保序减距变换。

点集:...是由……的各点（都在 x 轴上）之间彼此都保序拉大一段距离而得，示意图显示这增距变换使各在新位置的点到x轴任一定点例如原点的距离都比原来变大或变小了。任何非空数集A（或B）各元x（或y）到0的距离是|x|（或|y|），显然若A与B是同一集则|x|与|y|是同一函数；故有h定理3:A=B的必要条件是|x|=|y|。

书上x数轴的正半轴R＋各点x全都离开原位置地沿轴正向保序前移至新位置 x′=kx=x＋△x＞x＞0 处形成元是点 x′的Z＋，R＋显然就至少空出一没有点的正数位置x=a落在一切点（都在位置x′处）的后面——此x轴的固定位置与活动点之间的关系非常形象直观地表明R＋至少有一数a＜Z＋的一切元x′；故 Z＋的元 x′=kx 都变小为 x=x′/k＞0 组成 R＋≠Z＋，同理 R＋的元x都变小为y=x/k＞0组成 T≠R＋， 因 T至少有一y＜R＋一切x——发现有无穷小正数＜R＋一切x。其实应有h常识:“对于R＋从大到小、一个不漏的每一元x都有对应标准正数y=x/2＜x”就是说至少有一标准正数y＜R＋每一元x。将R＋换为“任何元为正数的A（各元 x都有比x大（小）的对应正数y）”就有革命的

h 定理 4:A 的元 x＞0 都变大（小）为 y（x）＞（＜）x 组成 B必≠A，因A必至少有一元x＜B一切元y（因B必至少有一元y＜A 一切元 x）。

证:①集是随元素的变换而变换的。A的元x:有的变大有的变小才有可能使变化前后的集相同，若其全都一致变大（小）为y（x），变化前后的集的元x与y就不可一一对应相等了。哪能有数集各元全都变大（小）了，而集却岿然不动的道理呢？！②据h常识由“对于B一个不漏的每一元y都有对应x（∈A）＜y”知 A 至少有一数 x＜B 每一（一切）元 y，同样…。 证毕。

故应有起码逻辑学常识:R＋各数x全都变大（小）为y(x)＞（＜）x所成之集不能还是原集R＋了，否则何来“一个不漏地全都变大（小）”？

3 “推翻”h定理2的症结:不知中学数学一直隐含重大病句

L=（0，10）=D＋[1，10）的一小部分 D=（0，1）各元 x 均保序不保距地变为y=10x∈L组成Z～D。问题是[2]指出Z≠L而只是L的一小部分。理由之一是～D的Z不可～L，没一配对法能使L各元x都有“配偶”y∈Z。按证明h定理2的反证法由h定理 1 易证 Z（～D）～L=D＋[1，10）不成立。 不可～L 的 Z 更≠L。据h定理2L不～DìL，故～D的Z≠L。L各元x的绝对值是|x|（x=y的变域是 L）＞0而 Z各元 y=10x的绝对值是|y|=|10x|（x=y/10的变域是D）≠|x|；据h定理 3Z≠L。D各元 x＞0均变大为y=10x组成Z，据h定理4DìL必至少有一元 x＜Z一切元y——显示Z≠L。 可见将元是x的D=（0，1）“拉长”变为元是10x的集Z与D增元变为元是x的L=D＋[1，10）是有根本区别的。

故自有函数概念几百年来一直公认的中学 “定义域为（0，1）的 y=10x 的值域=（0，10）”是将两异集误为同一集。 这使康脱误以为 D～L 而“推翻”h 定理 2。 同理“（0，1）～（0，k＞1）”等等，都不成立。 形如 y=10（y/10）=10x＞x＞0 的数 y都有对应正数y/10=x,称这类数为般正数。L内形如y=10x＞x∈D的正数y的全体组成了Z即L内全部般数组成Z。Z=L（般数）（L内所有般数组成的集）才是正确的，去掉“（般数）”就是中学重大错误。Z≠L揭示L内还有无穷多用而不知的不可纳入Z的非一般的“特异”数y无对应数y/10∈L。其实几百年函数“常识”:“对于一个不漏的每一正数x都有对应正数y=x/10比x小”就是说有正数y＜所有正数x——初数竟一直隐含此类重大病句！这是智力正常者都能一说就明的事实。关键是连文盲也知“一个不漏”的确切含义。

x轴各点x均保序变为点y=kx（k是有穷正数），x轴就保序变换成元为点y=kx的y=kx轴。

同序元概念:有序集如数轴A各数x在A内分别都有一定的大小“名次”。A各元x均保序变为y=g（x）（y是增函数）就得A的保序变换集B=g（A），x∈A在A中的大小名次与g（x）∈B在B中的大小名次是一样的，称y与x互为同序元。显然有

h定理 5:元为x的有序数集A保序变为B=g（A）～A，A=B的充要条件是恒有x=g（x）（凡同序元必相等）；显然必要条件:变换是保距变换（x轴与y轴的保序变换式y=kx（k是有穷正数）中的k=1时是保距变换，两轴若不全等就更不可重合相等）。

x轴所有正数点的坐标数组成R＋各元x均保序变大为y=10x＞x组成 U～R＋， 据 h 定理 5、4 等，U≠R＋即定义域为 R＋的y=10x的值域U≠R＋。

以上发现表明中学“R各元x都有对应 10x、x/10∈R”等等是一系列重大错误。由此可知:因“R各元x都有对应标准实数10x、x/10”故有部分10x∈U与x/10是用而不知的非一般的R外标准实数——推翻百年“R完备”论。详论见[2][3]。

4 近似常识凸显R只是标准实数全体的沧海一粟表明有标准无穷大实数＞R一切数——可视其为0而忽略的x→∞可取一切正数？

解恩泽等:“大凡一种理论体系，都可能潜伏着逻辑矛盾即悖论，发现悖论并设法消除之，往往会导致重大的科学革命。 ”（《潜科学》1992(2)，2 页）。 质量为 M=kx的地球（或其它星球）上一粒质量为x的沙子被风扬起，球的M就受到扰动而变为=kx＋（-x）≈kx——和式的末项-x可视为0而忽略，若x→∞则x与kx(k＞＞1固定不变)相比总还是等价于一沙子与地球相比，以致于可视x为0而忽略。可见x→∞也有相比下总≈0的另一面，科学极不发达期地球的极伟大性掩盖了它的极渺小性，数学极不发达期此x→∞的一面掩盖了其也有被限制相比下总距0太近的另一面。同样，定义域为R＋的取标准正数的

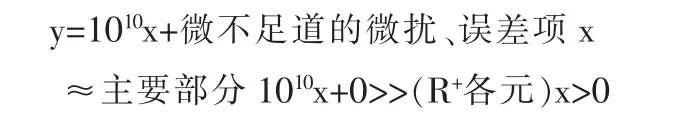
是说变域是R＋的误差项x（可→∞）＞0与y的主部相比实在是总距0太近了以致于可视其为0而忽略即说R＋各元x相比下全都是可忽略不计的极小正数。于是R＋只是正数全体的沧海一粟（y的首项可是10100x等等）——近似计算常识凸显y的变域K有元y＞＞R＋的一切元x。因“R＋各元x都有对应标准正数y与1010x、…”故一直存在用而不知的标准无穷大实数x＞R一切数，以及1/x＜R一切正数——标准分析与非标准分析等价的原因。人们在近似计算中不自觉地纠正了中学重大错误:K=R＋且含全部正数。关键是有起码数学常识:绝不可将可取一切正数的x视为0而忽略；且据h定理5等，R＋≠K。故“R各元x都有对应1010x、10100x、…∈R”是极重大错误。

若y的定义域改为是N（各元n都有对应标准自然数y与1010n、…）则上述近似常识凸显K有自然数元y＞＞N一切元n，N只是非0标准自然数全体Q的沧海一粟，中学的“N=Q”是以井代天错误。将根本不是N的一部分的K～N误为N的一部分使人“推翻”h定理2。

5 结束语

不识上述重大真相使数学一直被无穷现象中的假象与病态的集论迷惑而无法化解数学危机。详论见[1][2][3]。这表明数学家们在打基础的中学阶段就受到了影响自己一生的重大误导教育而又一直被蒙在鼓里，从而受害终生。例如使“天才数学家”康脱推出极荒唐的百年病态谬论“部分可=全部”。百年集论百年来浪费了亿万学生大量的宝贵时间（“时间就是金钱，…”）与精力以及亿万元宝贵学费。更要命的是它的重大误导作用:误导人推出更重大错误。育人课本的重大错误所造成的重大经济损失一点也不亚于经济建设中的重大错误所造成的经济损失，是否及时纠正，与每一个人的切身利益息息相关。

［1］黄小宁.真正科学常识否定5千年“常识”:没最大自然数——证实庞加莱百年前伟大科学预见推翻百年集论[J].科技信息，2011（27）.

［2］黄小宁.发现最小正数推翻百年集论消除2500年芝诺悖论——中学重大错误:将无穷多各根本不同的点集误为同一集[J].中国科技信息，2010（18）.

［3］黄小宁.“时空量子化”的关键:纠正数学课本一系列重大错误——证明实数轴有最小、大正数点推翻百年集论[J].科技信息，2011（17）.