基于LMI的主动悬架混合H2/H∞控制

陈建军，葛如海，王 斌

(1.江苏大学汽车与交通工程学院，镇江 212013;2.盐城工学院优集学院，盐城 224001)

近年来，线性矩阵不等式方法以其高效的求解而引起控制界的关注，成为鲁棒控制分析与综合的重要方法.基于LMI方法的混合H2/H∞控制因具有H2控制的优良品质和H∞控制的鲁棒性以及干扰抑制能力，同时又是一种便于处理的多目标控制，被广泛应用于悬架系统多目标鲁棒控制分析与综合中[1].

文献[1-3]中将车身加速度作为H2性能，将轮胎动载荷作为H∞性能，H2性能和H∞性能分别赋予不同权值后构成一个单目标函数，然后最小化目标函数，从而得到最优控制律.然而，对于实际问题，选择合适的加权系数并不容易，此外，在H∞性能中也没有考虑主动控制力阈值.针对上述问题，尝试将车身加速度作为H2鲁棒控制性能输出指标;将悬架动行程、轮胎动载荷和控制器作动力作为H∞鲁棒控制约束输出指标;综合考虑平顺性、操纵稳定性以及主动控制力阈值，将系统的性能输出归结为在给定抑制程度γ∞下的最优控制问题，避免加权系数的选择，然后，利用LMI方法进行处理.

1 1/4车辆主动悬架模型

1/4车辆主动悬架模型如图1所示.它由悬架弹簧和阻尼组成被动部分，而主动力F由液压伺服装置提供，ms为车身质量，mu为车轮质量，ks为悬架刚度，cs为悬架阻尼，kt为轮胎刚度，zs、zu、zr分别表示车身位移、车轮位移与路面位移.

图1 1/4车辆主动悬架模型

对应的动力学微分方程表示如下

选取状态向量

则二自由度模型的状态空间可描述为

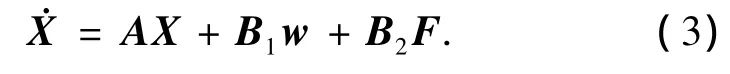
式中各系数矩阵

2 控制器设计

2.1 基于LMI的混合H2/H∞控制问题描述

混合状态反馈控制模型如图2所示，其中z∞和z2代表被控输出信号;y为测量信号，代表外部干扰信号;P(s)代表广义受控对象;K(s)代表所设计的控制器.系统的状态方程如下

式中:

图2 混合H2/H∞控制框图

由外部输入w到被控输出的闭环传递函数分别为TwZ2和TwZ∞，混合状态反馈H2/H∞可表示为设计一个控制器，并满足以下要求[4]:

①闭环系统渐进稳定.

②当w被看成是一个有限能量的扰动信号时，从干扰输入w到约束输出z∞的闭环传递函数的H∞范数小于给定的 γ∞.其中=，σmax表示一个矩阵的最大奇异值，γ∞代表干扰抑制程度.

根据文献 [5]，用LMI表示即为:

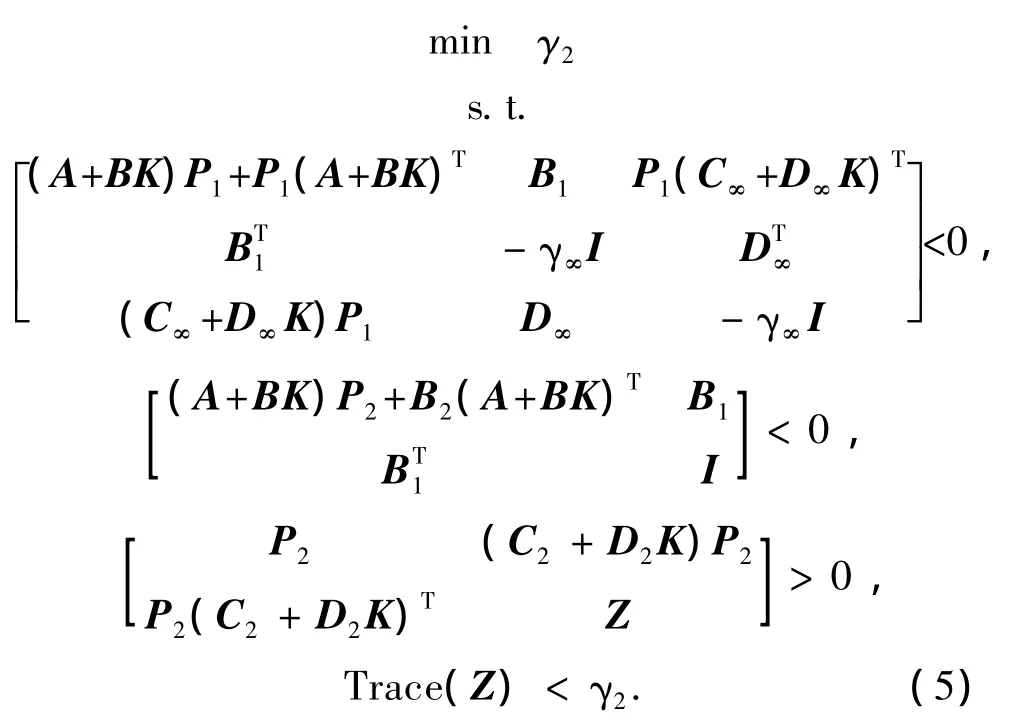
在上述模型的约束条件中，P1和P2是两个不同的对称正定矩阵，并且和控制增益K耦合在一起，这是一个非线性矩阵不等式问题 (双线性矩阵不等式BMI).为了利用线性矩阵不等式方法进行求解，引入约束条件X=P1=P2，因此，得到的结果具有一定的保守性.保守性的引进可以换来计算上的方便和有效，但如何估计由约束条件所带来的保守性大小，目前还缺乏有效的方法.

2.2 混合H2/H∞控制器设计

设计悬架首先考虑乘坐舒适性的要求，车身加速度¨zs是评价舒适性的主要指标.同时，兼顾稳定性的要求，轮胎与路面的动载荷kt(zu-zr)不能超过静载荷(ms+mu)g;又由于受悬架结构的限制，必须将悬架动行程zs-zu限制在一定的范围，以免撞击缓冲块而破坏乘坐舒适性[6-7].此外，考虑发动机功率的限制，液压伺服机构只能提供有限的主动力.因此，控制器的设计原则为在悬架动行程、轮胎动载荷和控制器作动力约束输出指标不超过相应范围的条件下，最小化车身加速度输出性能指标.而只要H∞范数小于预设的干扰抑制度γ∞就可以将其限定在一定的范围[8]，所以将悬架动行程、轮胎动载荷和控制器作动力定义为H∞约束输出指标，在此条件下优化车身加速度H2性能输出指标.综上，主动悬架的性能输出和归一化约束输出为则状态反馈控制律为路面激励用白噪声，其中，G0为路面不平度系数;U代表车速;w(t)代表均值为零的高斯白噪声.

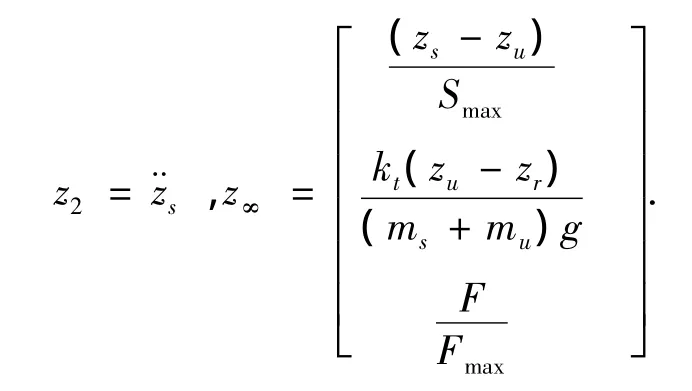
3 仿真与结果分析

为了检验控制效果，在MATLAB/SIMULINK环境下，参考文献[9]建立B级路面模型对被动悬架和主动悬架进行仿真对比计算.系统参数为:簧载质量为ms=372 kg，非簧载质量mu=45 kg，悬架刚度为ks=30 kN/m，轮胎刚度为kt=181 kN/m，悬架阻尼为 cs=1600 Ns/m，Smax=0.03 m，Fmax=1000 N，路面不平度系数为Gq=64×10-6m2/m-1，车速U=60 km/h，参考空间频率为n0=0.1 m-1，采样时间为0.01 s，仿真时间为5 s.

3.1 时域分析

通过对不同的标量γ∞求解相应的H2/H∞控制问题，可以分析系统H2性能和H∞性能的关系:两者之间相互竞争，牺牲系统的鲁棒性可以改进系统的性能.通常先求取最小的γ∞(代表系统的最优H∞性能指标)，然后，逐渐增大γ∞的值，求取满足约束输出且性能输出较好的K.这里取γ∞=0.2，然后，利用YALMIP工具箱求解线性矩阵不等式组求得K，再利用状态空间法便可以得到各性能参数的输出响应，图3～6分别为车身加速度、悬架动行程、轮胎动载荷和主动控制力的时域响应波形对比图.

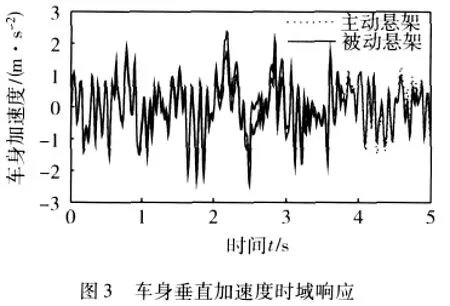
图6 主动控制力时域响应

可以看出主动悬架的控制效果明显，在悬架动行程和轮胎动载荷均有降低的情况下主动悬架的车身加速度明显小于被动悬架的车身加速度，同时由于在求解时将作动器最大输出力做了约束，输出控制力没有出现超过Fmax的现象，这样可以节省能量.各输出参数均方根对比图见下表1.

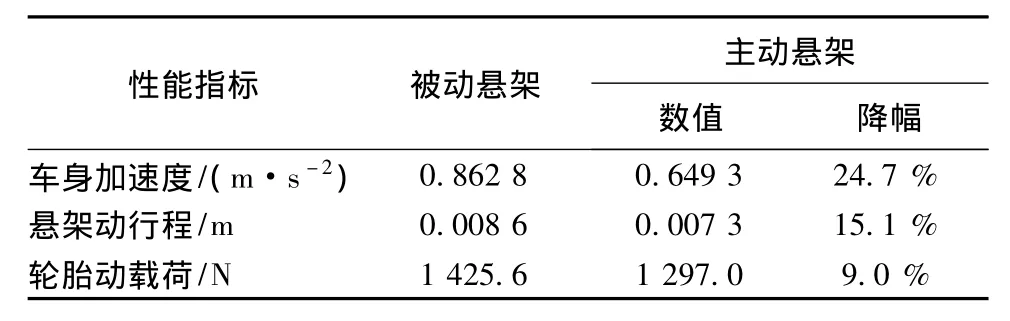
表1 时域均方根值表

主动悬架的各项性能指标均方根均低于被动悬架，其中车身加速度降幅最大，悬架动行程次之，轮胎动载荷降幅较小.分析可以发现，被动悬架的轮胎动载荷为1 425.6 N，大于静载1/3(1 390 N)，主动悬架的轮胎动载荷为1 297 N，小于静载1/3，轮胎有99.7%以上的时间不离地，根据3σ理论满足操纵稳定性的要求[1].

3.2 频域分析

车身加速度作为衡量舒适性的标准，不仅在时域上要求其幅值尽可能低，而且在频域内要求在人体最敏感的4～8 Hz内幅值尽可能低.图7和图8分别为车身加速度和轮胎动载荷的频域响应.

图7 车身加速度频域响应

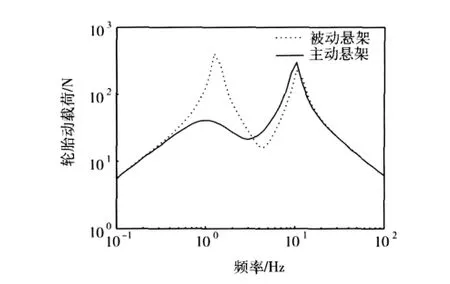
图8 轮胎动载荷频域响

从图7中可以看出主动悬架的平顺性在0.4～10.5 Hz的频率范围内以及第2个共振峰处均优于被动悬架;从图8中可以看出主动悬架在0.3～3.4 Hz频率范围内的操纵稳定性明显优于被动悬架，在高频区稍有恶化.

4 结论

以获得较好的平顺性和操纵稳定性为目标，将主动悬架的被控输出分离为性能输出和约束输出两部分，以H2范数描述性能输出，以H∞范数描述归一化约束输出.运用混合H2/H∞鲁棒控制理论结合线性矩阵不等式算法时，通常先求取最小的γ∞，然后通过逐渐增大γ∞的取值.即通过在H2性能和H∞性能之间取折衷，这样避免了加权系数的选择，在满足H∞约束输出指标的干扰抑制程度γ∞的条件下得到了最小化H2性能输出指标的最优状态反馈控制律.仿真和分析结果表明，采用的控制算法对车辆悬架的设计具有一定的指导意义和实际应用价值.

[1]罗铭刚.基于LMI的半主动悬架多目标输出反馈控制研究[D].重庆:重庆大学，2007.

[2]李以农，郑 玲，罗铭刚，等.汽车主动悬架H2/H∞多目标控制线性矩阵不等式方法 [J].重庆大学学报，2010，33(4):1-8.

[3]Lu J，Poyster M De.Multi-objective optimal suspension controlto achieve integrated ride and handling performance[J].IEEE，Trans.On Control Systems Technology，2002，10(6):807-821.

[4]张志勇，文桂林，钟志华.车辆主动悬架的混合H2/H∞最优保守性能控制 [J].汽车工程，2007，29(7):606-610.

[5]俞 立.鲁棒控制—线性矩阵不等式处理方法[M].北京:清华大学出版社，2002.

[6]HROVAT D. Survey of advanced suspension developments and related optimal control applications[J].Automatica，1997，33(10):1781-1817.

[7]Abdellari E，Mehdi D，M’Saad M.On the Design of Active Suspension System by H and Mixed H2/H∞:An LMI Approach [C].American Control Conference，2000.Proceedings of the 2000:4041—4045.

[8]陈 虹，马苗苗，孙鹏远.基于LMI优化的主动悬架多目标鲁棒控制 [J].自动化学报，2006，32(4):550-559.

[9]吴志成，陈思忠，杨 林，等.基于有理函数的路面不平度时域模型研究 [J].北京理工大学学报，2009，29(9):795-798.