用于优化机械加工参数的BP网络模型

滕荣华，谢晓燕

0 引言

随着工业化进程的进一步加快，基于BP网络模型下优化机械加工参数的网络模型研究热潮又一次兴起，这不仅是基于BP网络模型的改进，更主要的是基于智能优化机械加工参数的迫切需求。这是因为在进行机械加工时，不同毛坯的形位、尺寸以及装卡偏心都不尽相同，存在一定的误差，这些都可引起加工误差的产生（也就是我们常说的误差复映）。在实际的机械加工过程中，为减小误差复映所产生的误差，通常采用多次加工的方式，这是因为在每次的加工过程中我们都可以选取适当的加工余量进行加工。

目前，随着BP网络模型的进一步成熟和完善，完全可以利用BP网络的非线性全局映射能力、泛化能力以及强大的自学能力，通过学习人的优化经验，只要把加工的条件以及完成目标输入BP网络，就可以得到加工工件的加工次数、切削力以及加工余量等加工参数，实现基于BP网络模型的机械加工参数的优化。

1 改进的BP算法

1.1 标准的BP算法自身存在的缺陷

标准的BP算法主要存在的两个方面的缺陷，分别为训练时间过长和易陷入局部极小值。

1.2 改进的BP算法

遇到一些比较复杂的问题，用标准的BP算法来处理的话，由于其训练的速率小，因此需要比较长的训练时间，对于以上情况我们可以通过结合自适应学习率解决上述问题。可通过附加动量修正法帮助BP算法滑过误差的极小值，避免BP网络模型陷入局部极小值，其实现的主要途径是修正BP网络的权值。把结合自适应学习率与动量法的BP算法称为改进的BP算法。下面利用一个具体的例子来直观展现改进算法的优点。

实例1：有目标矢量1组和但输入矢量24组为：

目标矢量：P=-1:0.1:1；

但输入矢量：T=[-0.860 -0.025 0.345 0.456 0.660 0.580 0.465 0.376 0.242…-0.190 -0.453 -0.550 -0.420-0.168 0.056 0.045 0.356…0.410 0.366 0.105 -0.042-0.258 -0.345 -0.420]

分别使用BP算法、结合动量法以及改进的BP算法对实例1进行训练，在训练的过程中统一参数及网络结构。其中要求训练次数最多为8000次，目标输出与实际输出的误差平方和令其等于0.8。

BP算法训练的误差曲线如图1所示，其中，模型的学习速率设置为0.01。

结合动量法训练的误差曲线如图2所示，其中动量常数使用原始值。

使用改进的BP算法训练的误差曲线如图3所示，其中，动量常数以及学习速率都使用初始值。

从三幅误差曲线图能够看出，使用标准算法训练的次数多，效果最差；训练5600次后结合动量法完成目标要求；只训练了1600次，改进的算法训练便达到了要求。因此，使用改进算法具有最佳的效果。

图1 标准BP算法训练的误差曲线

图2 结合动量法训练的误差曲线

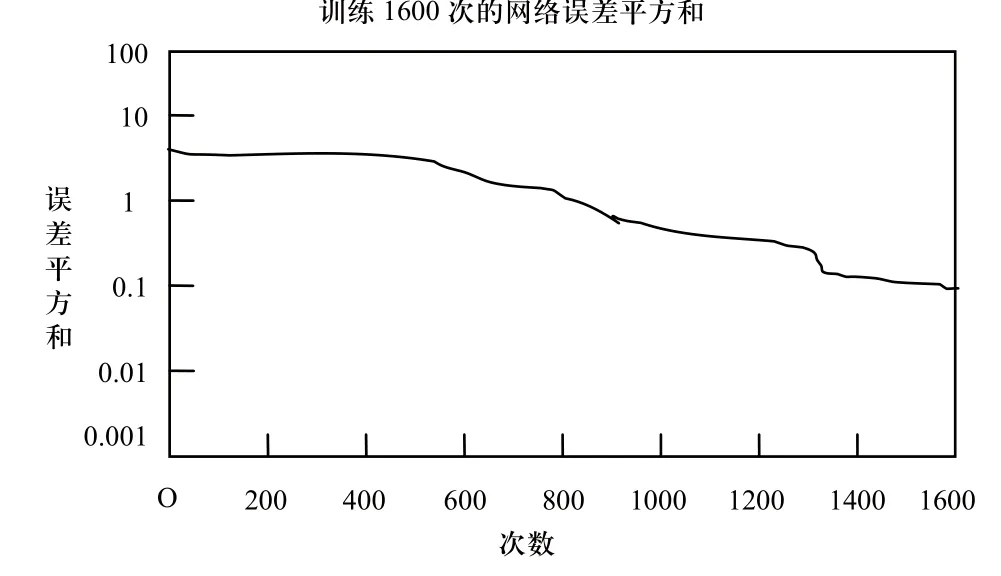
图3 改进的BP算法训练的误差曲线

2 毛坯工件的误差复映特点

未加工的毛坯工件A如图4所示，其外围近似椭圆形状，但存在一定的形状误差，我们令ap1和ap2分别表示刀具在椭圆长轴和短轴上的背吃刀量，分别用y1和y2表示让刀量，若加经过第一次加工后的机械工件仍有形状误差，则需继续加工。

图4 毛坯工件A的误差复映问题示意图

误差复映系数ε表示为：

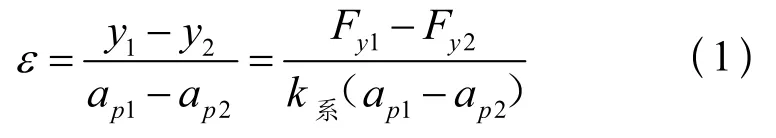
其中，Fy1表示椭圆长轴处的径向切削分力，Fy2表示椭圆短轴处的径向切削分力，而k系表示工艺系统的刚度。而刀削力Fy可表示为：

其中，与刀具前角等切削因素相关的系数用Cy表示，进给量用f表示，ap代表背吃刀量，加工的工件材料的硬度用HBS表示，y、x、n分别代表它们的指数，那么误差复映系数可表示为：

对车削进行近似，并令x≈1，则式（3）可表示为：

我们用QQ表示加工前工件的毛坯误差，用QH来表示加工完成后工件的误差，用ε1、ε2、ε3表示第1、2、3次工件加工的复映系数，那么我们可得出：

在上面的式（4）中，Cy由刀具的前角决定，在对同种类型的工件进行加工时，所使用的刀具相同，因此Cy不变。综合式（4）和式（5），我们可以得到：

通过式（6）能够得出加工完成后的工件误差与工件的硬度、进给量、加工次数、工艺系统的刚度以及毛坯自身的差异等存在复杂的非线性关系。从实际上来讲，如果采用的切深不同，加工完成后的误差就会不同。因此我们用P1、P2表示每次切深与总切深的比值，用Z表示加工次数。得出相关参数，其中，输入参数为k系、HBS、f、QQ以及QH，输出参数为P1、P2，然后对BP网络模型进行学习、训练，得出上述变量的非线性函数的逼近。

3 改进的BP网络模型的应用

3.1 Z值变换

实验中选取φ45 的铸铁、30的钢、40的钢以及铸铝等不同型号的棒料进行加工。在实际的加工过程中，会出现数值大小相差较大的变量，因此，在实验初期需要对所有的变量进行标准化，目的就是使每个变量处于同等重要的位置。可通

3.2 确定网络隐层数及神经元数

3.2.1 隐层数的确定

隐层数的增多会降低误差曲面梯度的稳定性，因此在解决实际问题时通常采用较少的隐层；但在解决存在不连续映射关系的问题时，如果使用一个隐层，无论增加多少个神经元，进行多少次训练，都到达不了目标误差，因此需要再增加一个隐层。经过大量的实验发现，一般采用两个隐层就能很好的解决问题，因此，通常情况下采用两个隐层。

3.2.2 隐层神经元数的选择

隐层神经元数的选择对整个网络来说显得极为重要，这是因为如果隐层神经元的数量太少，会导致不足匹配；而如果选择的神经元的数量太多，又会增加训练时间以及局部极小值的点数。通过大量的实验发现，隐层神经元数的选择应服从从输入层到输出层等比递减的金字塔规则，因此，多数的神经元应在第一层被选择。

3.3 训练和测试流程图

在测试过程中，先对Z值反变换然后再进行网络输出，初始权值在（-1，1）之间选，并用S1表示第一层神经元的个数，这样做的目的是在保证得到较好的训练结果的前提下尽量减少训练次数。其训练和测试流程如图5所示。

3.4 测试及其结果

3.4.1 测试

用训练集对改进的BP网络的测试结果如表1所示。其中EB表示加工前的误差，EE表示加工后误差的输入量。

图5 训练及测试流程图

表2 测试集对网络测试结果

用测试集对BP改进的网络的测试结果如表2所示。

3.4.2 测试结果

通过表1、2可看出，无论是使用训练集还是测试集对改进的BP网络进行测试，改进的BP网络都能实现较好的收敛性，达到目标误差的要求，可以很好地对机械加工中的参数进行优化。

4 结论

用改进的BP网络模型对机械加工参数进行优化，能避免过去纯粹依靠工人经验的盲目性，并通过自身的训练和学习能力，适应不同类型的机械工件的加工条件和要求，极大地提高了优化机械参数的质量和效率。

[1] ABDENNOUR A. Shortterm MPEG-4 video traffic predictionusing ANFIS[J].International Journal of NetworkManagement, 2010,15(6): 377-392.

[2] 吴晓莉, 林哲辉. MATLAB辅助模糊系统设计[M]. 西安: 西安电子科技大学出版社, 2008.

[3] DEMUTH H, BEALE M, HAGAN M. Neural networktoolbox for use with MATLAB user’s guide[M]. USA, MA: The MathWorks Inc, 2009.

[4] JIANG M, GIELEN G, ZHANG B, et al. Fast learningalgorithms for feedforward neural networks[J].AppliedIntelligence, 2008, 18(1): 37-54.

[5] 何强, 何英. MATLAB 扩展编程[M]. 北京: 清华大学出版社, 2009.

[6] 卢秉恒, 于骏一, 张福润, 等. 机械制造技术基础[M]. 北京: 机械工业出版社, 2008.

[7] LOTFI A Z, BERKELEY C. Fuzzy logic toolbox for usewith MATLAB user’s guide[M]. USA, MA: TheMathWorks Inc,2010.