输电铁塔中连续轴压杆计算长度系数的讨论

王如新，柳 超，刘中伟，江 帆

（1.辽宁省建筑设计研究院，沈阳110005；2.东北建筑设计研究院，沈阳11005）3.华东建筑设计研究有限公司，上海200012）

输电铁塔中的主杆通常是连续的构件，通过腹杆将其分为不同段，其主要受力形式为轴心受压。在设计结构时，常常将所计算的受压杆件从整体结构中分离出来，考虑结构其他部分对它端部的约束作用，并用计算长度来体现这种约束。在目前的铁塔规范设计中连续轴压主杆的端部约束仅考虑了不同腹杆布置的影响，对于上下段压杆对于中部压杆的支撑作用并未考虑，设计偏于保守。本文通过对输电线塔结构中抽取简化的理论分析模型，采用弹性弯曲屈曲分析的方法，分析了上下段压杆对于中部压杆的有利作用，得出轴心压杆受上下连续连接的压杆影响下的计算长度系数求解公式。

1 规范关于主杆计算长度规定

我国《架空送电线路杆塔结构设计技术规定》对于主材计算长度主要从腹杆的布置来考虑的，对于不同的腹杆布置，计算长度和计算回转半径都有所不同（见表1）。按最小轴布置，主材在两个面内节点重合，计算回转半径采用绕最小轴的，计算长度取节点间距；按照平行轴布置时，主材在两个面内无节点重合，其计算长度采用绕平行轴的，计算长度取1.2倍节点间距。

表1 主材计算长度表

不同腹杆的布置，主材的受力形式有所不同。按照最小轴布置时，主材的受力近似轴心受力构件，在规范里忽略了上下端压杆对它的有利影响，直接将实际长度取为计算长度。而对于按照平行轴布置时，由于每个面内的节点不重合，主材在节点处的受力为偏心受压，这会降低主材的承载能力，其计算长度有所扩大。

美国《输电铁塔设计导则》［2］对于两端具有中心轴力的主杆其计算长度系数取1，忽略上下段压杆的有利作用，计算结果偏于保守。

2 约束端柱的计算长度系数分析方法

将各种约束条件的压杆等效为铰接轴心压杆，此铰接轴心压杆的长度即是实际受压杆件的计算长度。图1大致表征了铰支端和约束端柱曲线的关系，AC长度为约束端柱的实际长细比L／r，AB长度为约束端柱的有效长细比L0／r，L0即为约束端柱的计算长度。计算长度与构件实际长度之间的关系是L0＝μL，其中μ为计算长度系数，图中计算长度系数可表示为

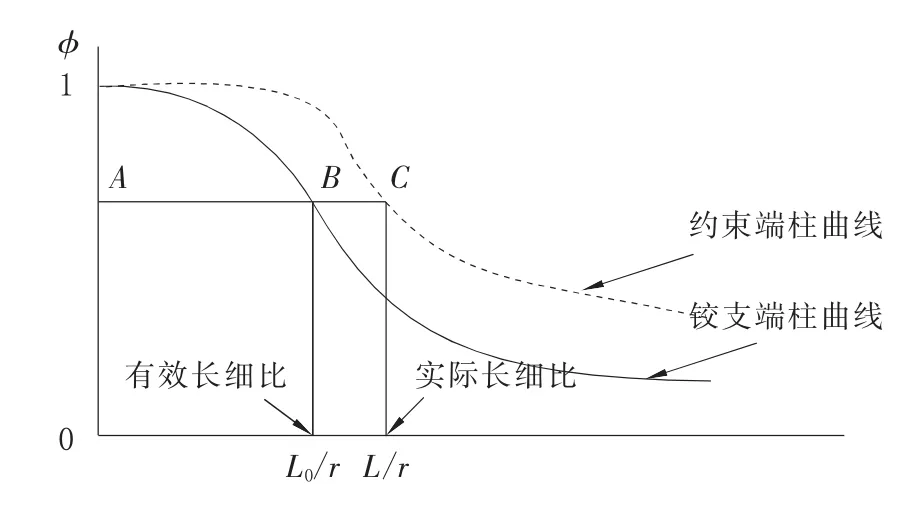
图1 杆端约束下计算长度

3 连续轴心压杆的理论分析

为了考虑上下段压杆对中部压杆的支撑作用，从输电铁塔中提取如图2的分析模型。

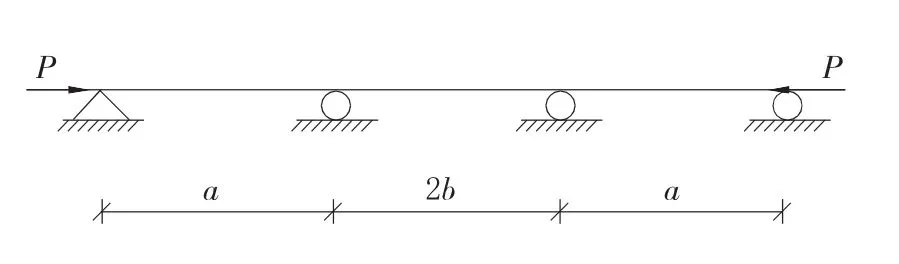
图2 理论模型

由于模型是对称结构，取半结构进行分析，上端简化为可平移但无转动的滑动支座，计算简图见图3。根据结构屈曲时存在微小弯曲变形的条件，先建立平衡微分方程，而后求解构件的分叉屈曲荷载，在建立弯曲平衡方程时需做如下基本假定：（1）构件是理想的等截面挺直杆；（2）压力沿构件原来的轴线作用；（3）材料符合胡克定理，即应力和应变呈线性关系；（4）构件变形之前的平截面在弯曲变形之后仍为平面；（5）构件的弯曲变形是微小的，曲率可以近似地用变形的二次微分表示，即Φ＝－y″。

图3 理论模型计算简图

由于Pv与M的大小关系不同对于平衡方程及求解也有所不同，分2种情况讨论。

（1）当Pv≠M 时

构件弯曲变形见图3，顶端挠度为v，当0≤x≤a时，平衡方程为：

其通解为：

根据边界条件，y1（0）＝0和y1（a）＝0，解得：

由于Pv≠M，B1＝0，边界条件要求A1≠0，故sinka≠0，所以

当0≤x≤a时，屈曲后的变形曲线为：

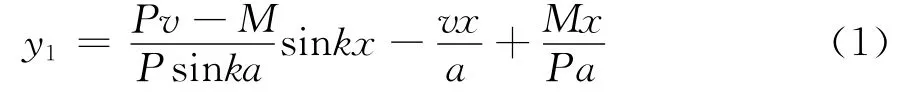
当a≤x≤a＋b时，平衡方程为：

令k2＝P／EI，

其通解为：

根据边界条件，y2（a）＝0、y2（a＋b）＝－v和y′2（a＋b）＝0，带入上式得：

由上述方程组得1－coskb＝Pv／M，故1－coskb≠0，上式的解为：

当a≤x≤a＋b时，屈曲后的变形曲线为：

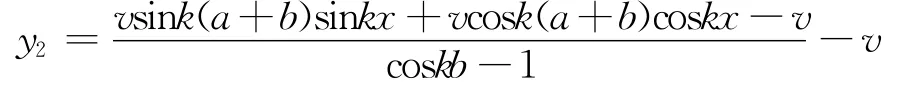
将式（2）中的M 值带入式（1），得出y1表达式为：

由B点变形协调条件y1′（a）＝y2′（a）＝及v≠0得到屈曲方程如下

由于1－coskb≠0，sinkb≠0，sinka≠0，上式可简化为ka＝kacotkacotkb－cotkb （3）

令α＝a／2b，l＝2b，因P＝π2EI／（μl）2故kl＝带入式（3），得到屈曲方程

（2）当Pv＝M 时

构件弯曲变形图见图3，顶端挠度为v，当0≤x≤a时，平衡方程为

通解为

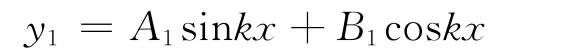
根据边界条件，y1（0）＝0和y1（a）＝0，带入上式解得

在0≤x≤a范围内，杆件产生如图3变形，并使屈曲荷载最小，需要ka＝π。变形及两屈曲荷载与两端铰接轴心压杆相同。

当x≥a时平衡方程与0≤x≤a相同，但变形曲线不同。

通解为：

由边界条件y2（a）＝0，y2（a＋b）＝－v 和y′2（a＋b）＝0，可得：

由式（5）中sinka＝0，故coska≠0，求解上式得：

在x≥a范围内杆件产生如图3变形，并使屈曲荷载最小，需要此段kb＝π／2，变形及两屈曲荷载与一端铰接一段滑动轴心压杆相同。

由于两段k相同，故

此情况下各段杆件之间无支撑作用，即μ＝1，此时的α＝a／2b＝1，这种情况也满足式（4）。

以不同的α值带入式（4）后，即可得到相应的计算长度系数μ，绘出μ－α曲线，见图4，当α接近0时，两端联系杆对中间试验段压杆的转动约束限制作用越来越强，μ＝0.5意味着端部的约束作用近似为刚接；当α接近1时，两端联系杆对中间压杆几乎无限制作用，μ＝1表示着端部的约束作用近似为铰接；在（0，1）区间里，压杆的计算长度小于1，说明端部的联系杆件对试验压杆承载力有一定的提高作用；当α大于1时，μ值也大于1，如α＝1.5时，μ＝1.30，结构破坏不再是中间的轴心压杆，而是上下段的压杆发生破坏，同样承载力较强的中间压杆对于上下段压杆有一定支撑作用；式（4）在上下段压杆长细比相同的情况下得出的，实际结构中上下段压杆的长细比并非一致，在此情况下，较安全地采用长细比较大的压杆计算α系数，计算的μ系数也是可靠的，式（4）的应用范围可以扩大了任意的连续轴压杆。

图4 μ—α曲线

4 结语

（1）上下段压杆对于中间的压杆支撑作用是有利的，而且随着α系数的增加，约束作用减小，中部压杆的端部约束在刚接和铰接之间变化，当α系数超过1时，屈曲破坏部位变为上下段的压杆，中部压杆同样对其有支撑作用。

（2）本文主要考虑了上下段压杆的影响，忽略了水平位移的影响，按照式（4）的公式仅可以计算不考虑水平位移下轴心受压主杆的计算长度系数。

（3）公式（4）是在上下段压杆长细比相同的情况下得出的，对于上下段压杆长细比不相同时，可取二者中长细比较大的压杆来计算α系数，求得的计算长度系数更可靠。

［1］DL／T 5154－2002，架空送电线路杆塔结构设计技术规程［S］.

［2］ANSI／ASCE10－1997，Design of Latticed Steel Transmission Structure［S］.

［3］陈骥.钢结构稳定理论与设计［M］.3版.北京：科学教育出版社，2006：10－15.