复合墙板承载力计算公式分析
李九阳,窦立军,王 莹
(长春工程学院土木工程学院,长春130012)
0 引言
复合墙板是由内、外两层钢筋混凝土板中间夹保温材料组成的一种新型墙体材料,钢筋桁架连接的复合墙板采用钢筋桁架穿过保温层连接墙板内叶、墙板外叶形成整体。钢筋混凝土层与保温材料层是物理力学性质相差较大的2种材料,受力后截面应力情况比较复杂。因此其承载力计算不能完全采用普通混凝土受弯构件的承载力计算公式。利用有限元程序进行多个试件的承载力试验模拟,依据混凝土受弯构件的计算公式,分析得到了复合墙板的承载力计算公式。
在承载力计算之前,首先需要确定墙板截面的应力分布类型。钢筋桁架作为3层材料的连接件,起着传递剪力的作用。根据连接件刚度的不同,截面的应力类型可以分为3类:3层材料之间无共同作用,部分共同作用和完全共同作用。无共同作用的截面没有连接件或连接件的刚度很小,可以近似认为上下混凝土层之间仅有保温层,不能传递剪力,在均布荷载作用下相当于两块跨度相同曲率相同的独立板;对于部分共同作用的墙板,连接件在剪力作用下会产生滑移,截面的平衡分析必须考虑应变差,连接件传递的剪力大小与其刚度有关;在完全共同作用下的墙板内,连接件的刚度足够大,上下层混凝土之间不会发生相对滑移,在弯矩作用下相当于整体截面板受力,沿截面高度的应变分布为一条连续直线。3种类型的墙板在弯矩作用下的应变分布分别如图1(a)、(b)、(c)所示。
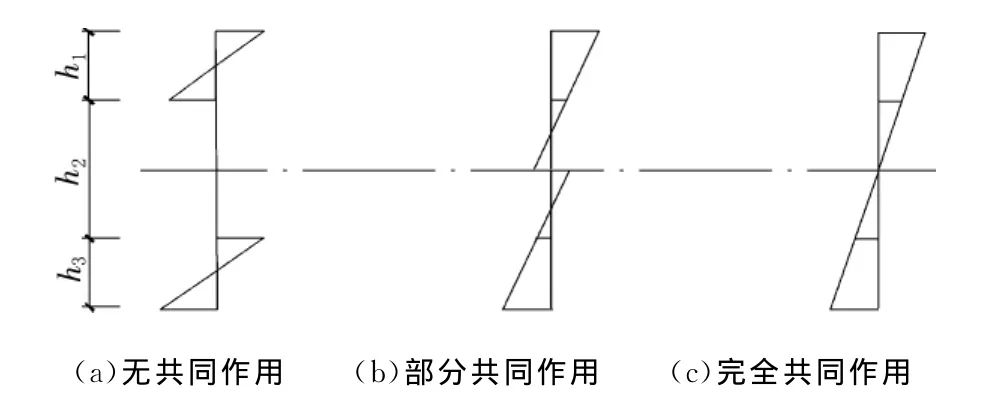
图1 复合墙板截面应变分布图
对于钢筋桁架连接的复合墙板,在钢筋桁架刚度足够的条件下,通过理论分析与试验验证,截面应变符合图1(c)的应变分布,即符合平截面假定。
其二,钢筋桁架连接的复合墙板承载力计算公式参考普通钢筋混凝土构件的理论,在受拉区纵向钢筋受拉形成拉力,受压区混凝土和受压钢筋形成压力,拉力和压力形成极限弯矩。因此按照墙板实际组成,利用有限元程序计算均布荷载作用下墙板各材料的应力,分析受压混凝土、受压钢筋、受拉钢筋,三者发生破坏的条件,建立承载力计算公式。
1 有限元计算材料应力
1.1 有限元模型建模
第1步,创建单元。建立2种不同的单元。墙板内、外叶、保温材料均属于体单元,选用Solid中的concret 65单元(保温材料材料属性不同);墙板中钢筋网、钢筋桁架用钢筋选用Link中的3Dfinit stn 180线单元。
第2步,定义线单元截面特性。
第3步,定义材料。定义混凝土、保温材料、钢筋3种材料的弹性模量、泊松比。
第4步,建模。创建节点,构筑体单元,复制小单元构成整块墙板;创建线单元,创建钢筋网架和桁架的杆件单元,复制构成钢筋网与钢筋桁架杆单元模型。
第5步,施加约束与加载。选取4个约束的位置,分别限制X、Y、Z3个方向的移动。施加均布荷载。
第6步,求解。
第7步,后处理。
1.2 确定破坏极限弯矩
墙板的破坏标志有4种:受压区混凝土压碎破坏、受压区钢筋屈服;受拉区混凝土开裂破坏;受拉区钢筋屈服破坏;最大挠度超过限值l/200,发生变形破坏。按照试件的实际截面构成,根据有限元计算结果,判断哪种材料先达到破坏,则可由该种材料强度确定破坏时的极限弯矩。
在课题研究中,按照工程实际及构造要求,在墙板内、外叶混凝土层双向配置Φ5@100冷轧带肋钢筋,按照实际位置放置竖向、水平钢筋桁架,直径按照等效原则换算成Φ8。有限元计算结果表明,受压区混凝土最危险。按照荷载—内力—应力线性关系,可以判断受压区混凝土应力首先达到抗压强度而破坏。因此将有限元计算时输入的荷载值乘以混凝土的轴心抗压强度设计值与混凝土的应力的比值即可得到墙板破坏时的极限荷载,从而可求得墙板破坏的极限弯矩。
1.3 试件极限承载力
有限元计算时按照热工计算和构造要求确定了2组常见墙板的截面构成,按照钢筋桁架间距不同设计了2组共15个试件,试件工况组合见表1,墙板中受压区混凝土应力及计算的极限荷载Qmax见表2。

表1 试件工况组合表

续表1

表2 墙板所能承受的极限荷载Qmax
已知作用在复合墙板上的均布荷载,通过不开洞墙板Mxmax、Mymax内力公式可以计算出复合墙板在X和Y方向上的破坏时的极限承载力弯矩,见表3。

表3 墙板极限承载力弯矩

续表3
2 承载力计算公式
2.1 公式推导
按照受压区混凝土破坏,参考普通混凝土受弯构件承载力计算公式M =α1fcbx(h0-0.5x)=α1fcbxγsh0,建立墙板理论极限承载力的计算公式模型为:

受压区高度简化成墙板内或外叶厚度,由此产生的误差在内力臂系数γs中调整。
式中:h3—— 受压侧墙板厚度,即内(外)叶墙板厚度;
h0——截面的折算厚度,按照惯性矩相等的原则计算;
γs—— 内力臂系数。
将极限弯矩、截面参数、材料强度带入式(1),可求得内力臂系数γs,其计算值见表4。
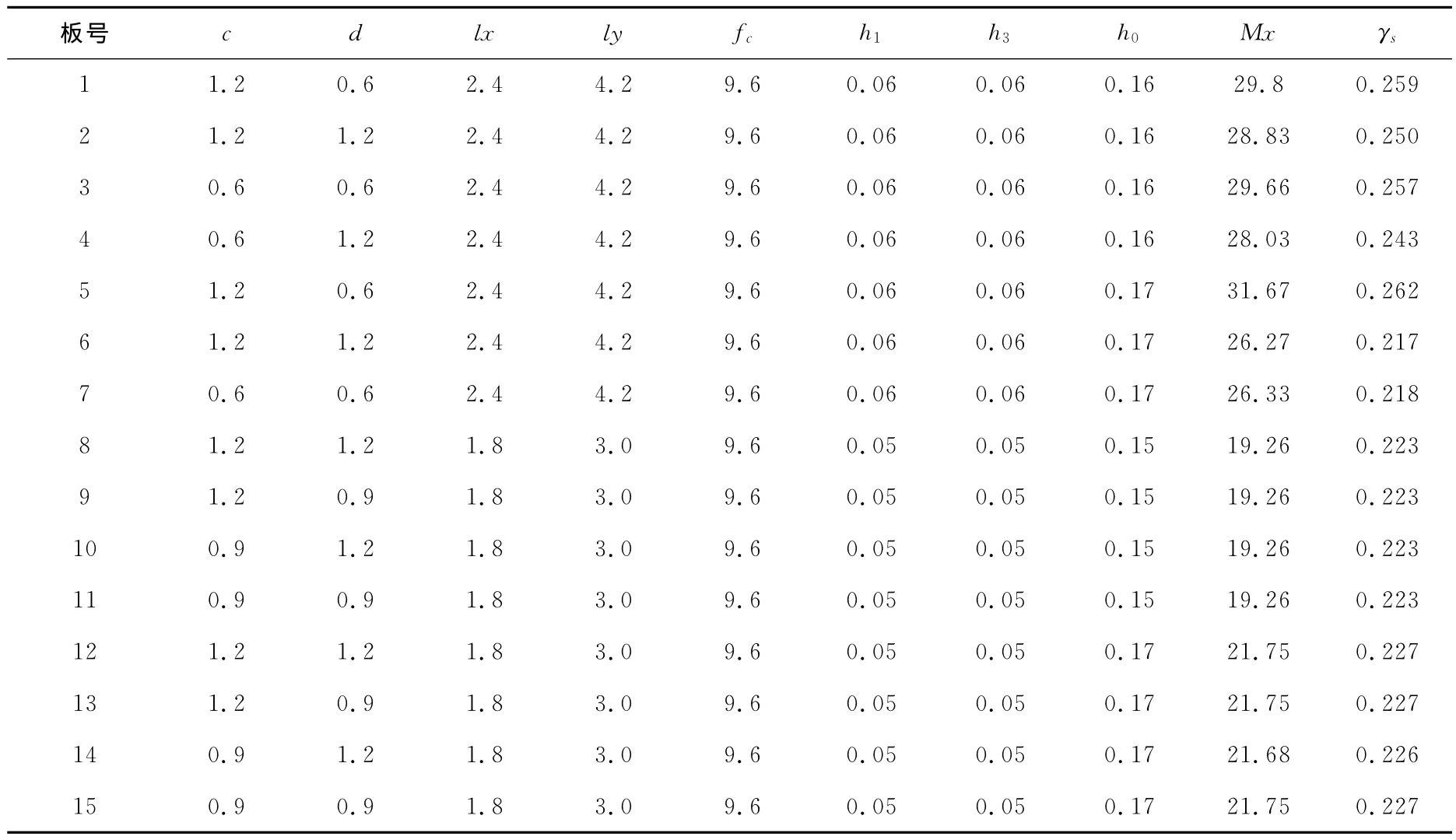
表4 内力臂系数计算表
在研究过程中,考虑影响内力臂系数的因素有:墙板内、外叶厚度h1、h3,截面的折算厚度h0,水平、竖直桁架的间距c、d,墙板的尺寸L、H。由于考虑到桁架间距对系数的影响较小,所以将cd/LH作为修正系数公式的一个变量。将h2(保温层厚度)和h对修正系数的影响组合成一个变量h2/h。在回归后,发现误差较大,考虑到墙板内、外叶厚度h1、h3较小,所以将墙板内、外叶厚度h1、h3之和作为一个因素,与截面高度h比值作为一个变量(h1+h3)/h作为一个影响因子,其中h为墙板截面高度。因此假定了γs公式模型为:

其中α、β、δ为回归系数。
按照一次线性函数,利用Matlab程序,回归得到系数,通过程序的误差观察,以及对公式的进一步检验。最后内力臂系数γs公式为:
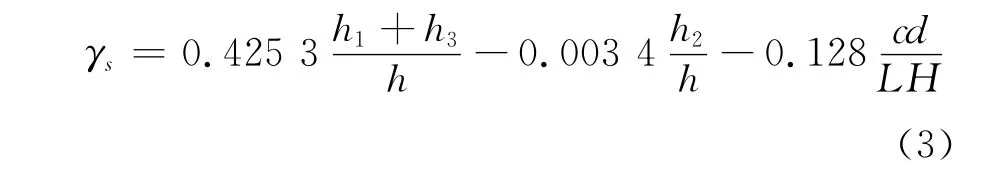
按照式(3)计算的内力臂系数γs与实际内力臂系数进行偏差分析,偏差率见表5。

表5 内力臂系数误差表
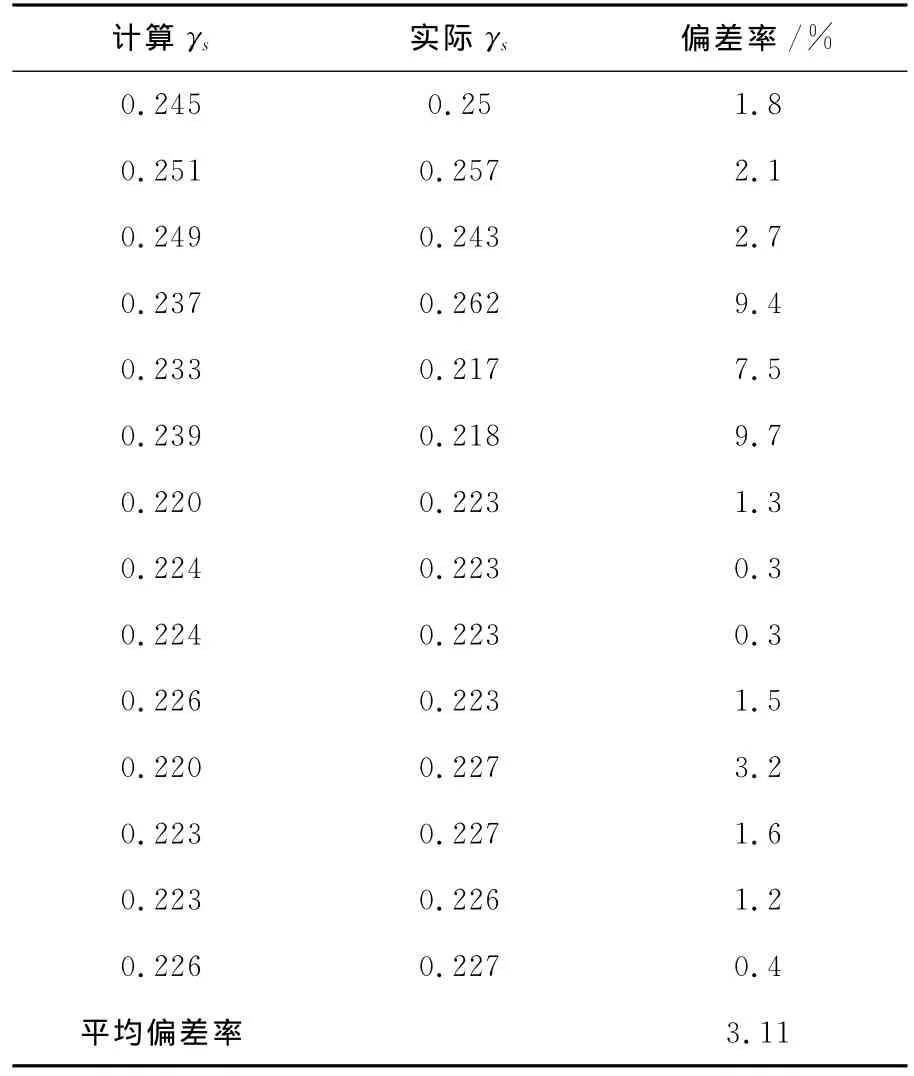
续表5
公式的偏差率3.11%,小于10%,所以此公式可以作为内力臂系数的计算公式。故复合墙板截面的受弯极限承载力计算公式为:

式中:h3——受压区混凝土厚度;
h0——墙板夹层截面折算高度;
h2——保温层厚度;
h——墙板截面高度;
c——水平桁架间距;
d——竖直桁架间距;
L——墙板板宽度;
H——墙板板高度。
2.2 公式适用范围讨论
(1)该公式仅适用于墙板受压区混凝土压碎破坏的破坏类型。对于钢筋屈服破坏,受拉区混凝土开裂破坏等其他破坏类型均不适用;
(2)lx≤0.5L,此公式是在墙板跨中正弯矩发生破坏时得到的。如果lx>0.5L时,支座处负弯矩将大于跨中最大正弯矩,为防止支座外墙板所受弯矩过大以及支座处负弯矩造成的破坏,lx尺寸不宜过大。
(3)墙板尺寸L、H 应用满足下述范围:L(3 000,4 800),H(3 000,4 800)。
[1]王爱民.密肋复合墙体在竖向荷载作用下受力性能有限元分析[J].工业建筑,2006(11):62-66.
[2]李九阳.夹芯复合墙板在水平荷载作用下变形的有限元分析[J].工业建筑,2010(12):87-89.
[3]Jiuyang Li.Finite element analysis of displacement of composite wall cladding under wind load[C]//ICETCE,2011.
[4]Jiuyang Li.Analysis of deformation of composite wall cladding panel[C]//ICECE,2011.

