采用模糊综合评判法的电缆过路管敷设模型

朱立蓉，吴 炜，李露莹，李昊扬，袁 喆

（

1.上海电力公司市北供电公司，上海200072；2.上海浦海求实电力新技术有限公司，上海200090；3.天津大学智能电网教育部重点实验室，天津300072）

随着经济的快速发展和大规模的城市建设，被称为“空中视觉污染”的城市上空架空线入地改造被提到了新的高度，特别是跨越城市快速路及区域主干河流的架空线改造势在必行，对电力过路管的敷设原则和敷设适应性提出了新的挑战。目前，国内对电缆保护排管的建设模式研究主要为道路排管，对于过路管的敷设适应性原则和发展模式鲜有研究，使目前过路管规划建设方向不够明确，更没有针对具体区域的过路管的量化敷设原则。

另外，由于各个地区的经济发展、负荷特性和负荷发展趋势各有特点，电力排管敷设现状及架空线入地改造等因素都将影响着过路管的敷设数量，为避免跨越城市主要道路和河流重复施工影响城市正常运转，因此在建设过路管之前，必须对该区块进行深入的分析和科学的规划，提出过路管量化敷设的原则，有效地指导过路管规划建设发展方向和发展模式，最终获得电力和全社会经济、社会效益最大化。

在明确敷设电缆过路管的用地性质及有无电缆排管等基础条件后，可通过评判方法从众多种敷设方案中确定一种最为合理经济的敷设方案。由于影响敷设方案的因素众多，所以本质上这是一个多指标的综合评判问题。本文尝试使用模糊综合评判的方法对电缆过路管的敷设模型进行研究。

1 模糊综合评判

模糊综合评判方法是从多个指标对被评价事物的隶属等级状况进行综合性评判的一种方法，它把被评价事物的变化区间做出划分，又对事物属于各个等级的程度做出分析，这样就使得对事物的描述更加深入和客观，故而模糊综合评判方法既有别于常规的多指标评价方法，又有别于强制的打分方法［1］。

1.1 评判模型

模糊综合评判法包括以下几个要素［2］。

（1）因素集。这里的ui是被评判事物的指标，表明从哪些方面来评判描述。

（2）评判集。

这里的评语vi是指对被评判事物变化区间的一个划分，即评判等级。专家针对方案某一因素的初始评判结果即为某一评语，本文方法正是利用这一模糊评判的手段来避免精确评判的不确定性。

（3）方案总数l和专家总数h。

（4）方案评判矩阵，将针对各个方案所收集的专家评判结果进行整合，即可形成各个方案的评判矩阵Rk，其中，1≤k≤l。

此矩阵表示针对方案k在因素集U中的因素ui对应于评判集V中的评语vj的隶属关系。其中，模糊关系矩阵中的数值由下式确定：

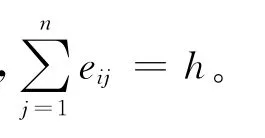
1.2 评判方法

针对上述模型，若可确定因素集U的权重向量A1×m，则可以输出一个评判结果向量Bk。

其中o是一个合成算子。从理论上说，算子有很多，此处使用加权平均型算子（﹒，＋）［3］，该算子在使用中的计算方法如下：

该方法不仅考虑了所有因素的影响，而且保留了单因素评判的全部信息，是模糊综合评判中常用的算子之一。选择了合成算子之后，将权重向量A与模糊矩阵R合成即得到该方案的模糊评判结果向量为Bk。针对l个方案要重复评判l次，以进行结果对比。

1.3 模糊评判数量化

若要将模糊的评判结果数量化，则需首先确定评判集V的数量化结果G

然后将其与针对某一方案的评判结果向量Bk进行加权平均处理，从而得到最终结果Ck。具体的处理方法是：

该模糊评判方法中有三个量需通过专家意见收集来获取，分别为Rk、A和G。其中，Rk可由专家针对某一个方案的评价意见直接得出，A和G则需综合各个专家意见方可得到，具体可采用Delphi法［4］等方法，此处不加赘述。

2 电缆过路管敷设问题分析

电缆过路管由于敷设地区的用地性质的不同，负荷水平的不同，以及现状条件有所差异，在进行评判之前应该分类处理，这样才能使评判有意义。对不同类别的过路管敷设进行模糊综合评判，得到可能的众多方案中最适合该方案的一种。过路管的分类如图1所示。

（1）由于缺乏具体的过路管敷设原则和敷设规划，过路管的敷设具有很大的随机性和不确定性，过路管用孔数种类很多，过路管敷设无量化的原则指导。

（2）路口过路管的敷设数量与有无电缆排管关系密切。如果道路上有电缆排管敷设，过路管的使用量会相应减少；但电缆排管代替不了过路管。

（3）过路管敷设孔数与负荷性质有密切关系，商业区路口过路管的用量高于居住区。居住区根据建设年代的不同，过路管的敷设有一定的差别，老型居住区过路管敷设量较少。

（4）随着商办区和居住区供电可靠性要求逐渐提高，智能电网建设迫在眉睫，现状过路管敷设中往往未考虑留有一定的裕量及检修孔。

（5）路中过路管布置与有无排管、区域用地性质关系不大，最大实用性孔数为4孔。

由现状的分析可以看到，路中过路管的情况比较简单，下面将只讨论路口过路管，以下提到的过路管均指路口过路管。

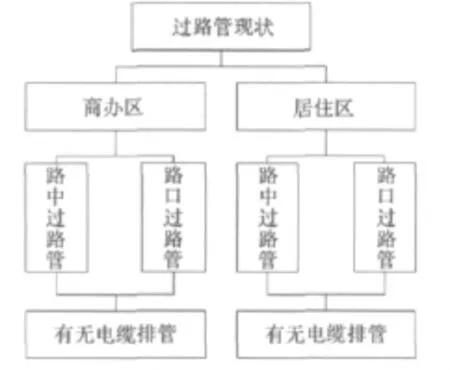
图1 过路管现状分类Fig.1 Category of cross road pipe

3 基于模糊综合评判的电缆过路管敷设模型

由于目前过路管的敷设没有统一的标准、对于过路管敷设的评判受到众多因素的影响，模糊综合评判能够较好的适应这类问题，将多指标的问题进行定量的评价，并客观的体现专家意见。首先要建立一个针对过路管敷设的评价指标体系，见图2。以便在众多可能的敷设方案中得到一个最符合环境要求并且经济可行的方案。

3.1 确定因素集

因素集即为直接参与评判的指标。对于过路管的敷设方案可以从三个方面分析。

4）胆道支架：支架的材质包括塑料类、镍钛合金类、不锈钢类。该三类支架植入后行MRI检查不会发生移位、致病性发热。不锈钢类支架在植入部位及附近行MRI检查可能产生伪影，影响图像质量。

（1）方案与环境因素的契合度

由于商办区用电需求明显大于居住区，其通过的电缆条数一般也大于居住区，因此过路管用量也会较大；另外有排管经过的路口，原则上过路管的用量应少于无排管通过的路口。

（2）方案与技术要求的符合度

根据上海习惯性施工方法，若电源方向为东西方向，则道路南侧为电缆和过路管的主要敷设方向，北侧则为次要敷设方向；若电源方向为南北方向，则道路东侧为电缆和过路管的主要敷设方向，西侧则为次要敷设方向。在次要敷设方向，应尽量减少电缆迂回敷设，一般要比主要敷设方向过路管数量少。此外，该地区负荷发展的预期也是影响过路管敷设孔数的选择。

（3）方案的工程经济性

过路管敷设孔数直接影响工程成本，同时，敷设孔数的多少也决定了施工土方以及土地资源的占用等方面问题。随着智能电网建设的快速发展，为智能通信和检修预留一些孔也是必要的。

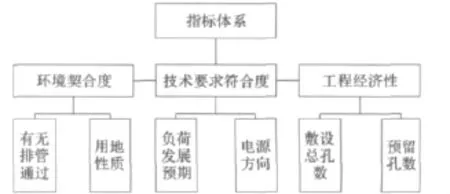
图2 过路管敷设评判指标体系Fig.2 Evaluation index system of cross road pipe

3.2 计算各分类中方案的模糊结果向量

对过路管的各种分类，分别用模糊综合评判来计算其结果向量。对各个分类分别进行模糊综合评判，在众多可能的方案中确定一种最优方案。由专家打分确定模糊关系矩阵是最关键的一环，必须由经验丰富的专家认真确定，从而保证整个评判的有效性和可信度。

3.3 计算评判结果向量确定敷设方案

对可能出现的几个方案得到的评判结果向量进行加权计算，得到一个综合得分并进行排序。最终得出该种情况下过路管敷设方案。

4 算例分析

以上海市北商办区为例，考虑已存在道路排管敷设的路口作为算例分析对象。现有四种针对某商办区路口的实际过路管敷设方案：方案1在路口东、南、西、北四个方向敷设过路管的孔数分别6、8、6、6；方案2在路口东、南、西、北四个方向敷设过路管的孔数分别6、8、8、6；方案3在路口东、南、西、北四个方向敷设过路管的孔数分别6、8、6、8；方案4在路口东、南、西、北四个方向敷设过路管的孔数分别6、8、8、8。根据所选定的评判指标对四个方案进行评判，选择一个得分最高的方案作为最终的商办区路口过路管敷设模型。

4.1 评判的初始条件

在进行模糊评判之前，首先确定评判的因素集和评判集。

（1）因素集。

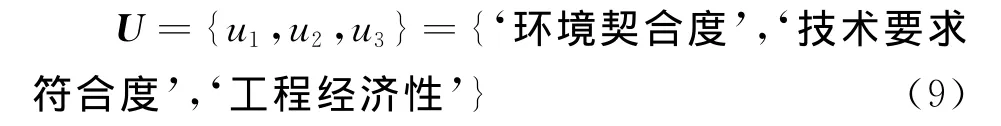
（2）评判集。

（3）方案总数l＝4，专家总数h＝10。

然后，利用Delphi法对专家意见进行统一，从而得出因素集权重及评判集数量化对应结果。

（1）由于‘技术要求符合度’相对更为重要，而‘环境契合度’与‘工程经济性’重要程度相当。因此权重向量为：

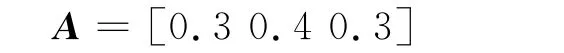
（2）评语数量化结果为｛优，良，中，差｝＝ ｛90，80，60，50｝，故

4.2 方案评判

在此基础上，即可针对各个方案进行评价，算例只给出方案1的详细计算过程，其他方案则直接给出评判结果。

（1）由10位专家打分为方案1进行评价，并确定模糊关系矩阵。

表1所示为10位专家对于因素集中的指标进行打分的情况。例如：10位专家中有6人认为方案1的‘环境契合度’这一指标可以评为‘优’，那么对应表格中填写‘6人’。

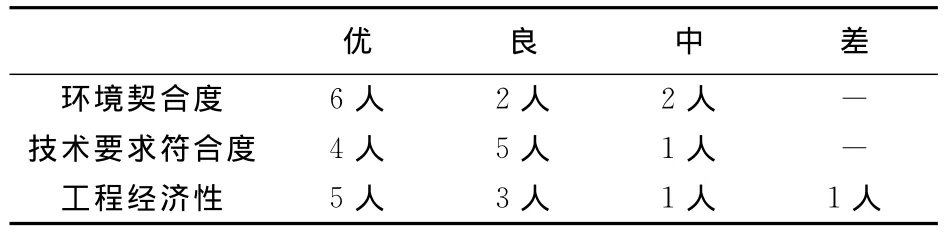
表1 方案1专家打分情况Tab.1 Expert evaluation results for project 1

（2）得到专家打分表之后，则可得到方案1的模糊关系矩阵。

（3）用加权平均型算子得到评判结果向量：

（4）将评判结果向量转化为最终结果，可得C1＝81.4。

方案2和方案3的计算过程类似，其评判结果向量分别为。

方案2：B2＝ ［0.37 0.44 0.16 0.03］

方案3：B3＝ ［0.27 0.35 0.35 0.03］

方案4：B4＝ ［0.34 0.29 0.34 0.03］

分别计算得到的最终结果分别为：C2＝79.6，C3＝74.8，C4＝75.7。

将评判结果向量转化为用单一数值表示的最终结果的得分可见方案1得分最高，因此选取方案1作为商办区有排管时的过路管敷设模型，见图3。

细化分析原因有如下三点：

①过路管敷设孔数多寡与电源方向相符；

②非电源方向已存在排管敷设的方位过路管孔数经济合理；

③方案整体经济性与预留余量协调合理。

图3 商办区有排管通过时过路管敷设结果Fig.3 Result of laying of cross road pipe in business area

5 结语

本文将模糊综合评判方法应用于电缆过路管敷设模型的研究中，很好地适应了评判指标的不确定性，并且在深入客观地描述电缆过路管敷设方案的同时，为敷设方案决策提供理论依据。通过引入模糊综合这一数学方法，使得传统电缆敷设中定性问题定量化，对电缆过路管的施工和管理具有实际意义。

［1］ 王巨川，章前，王刚（Wang Juchuan，Zhang Qian，Wang Gang）.多指标 模糊综合评判 （Multi－targets problem by fuzzy comprehensive evcaluation）［J］.昆明理工大学学报（Journal of Kunming University of Science and Technology），1998，23（4）：69－71.

［2］ 邹春伟（Zou Chunwei）.道路工程中的模糊综合评判法（Applications of fuzzy comprehensive assessment in technology of highway engineering）［J］.安徽建筑工业学院学报：自然科学版（Journal of Anhui Institute of Architecture ＆Industry），2004，12（1）：74－78.

［3］ 葛少云，阎大威，董智（Ge Shaoyun，Yan Dawei，Dong Zhi）.基于模糊综合评判的城市电网电缆化改造（Urban electric network cabling reconstruction based on fuzzy comprehensive judgment）［J］.现代电力（Modern Electric Power），2005，22（3）：37－40.

［4］ 刘学毅（Liu Xueyi）.德尔菲法在交叉学科研究评价中的运用（Delphi technique in the assessment of interdisciplinary research）［J］.西南交通大学学报：社会科学版（Journal of Southwest Jiaotong University：Social Sciences），2007，8（2）：21－25.

［5］ 杨永萍，李宝栋，常文春（Yang Yongping，Li Baodong，Chang Wenchun）.基于模糊综合评判方法的研究及应用（Study and application of fuzzy synthesize judgment method）［J］.兰州工业高等专科学校学 报 （Journal of Lanzhou Polytechnic College ），2006，13（3）：49－52.

［6］ 张晓平（Zhang Xiaoping）.模糊综合评判理论与应用研究进展（Advance in fuzzy comprehensive evaluation methods theory and application）［J］.山东建筑工程学院学报（Journal of Shandong University of Architectural and Engineering），2003，18（4）：90－94.

［7］ 王道勇（Wang Daoyong）.模糊综合评判的失效与消除（Lost efficacy and its removal in fuzzy synthetical judgment）［J］.系统工程理论方法应用（Systems Engineering－Theory Methodology Applications），1998，7（2）：66－69.

［8］ Wang Xizhao，Chen Bin，Qian Guoliang，et al.On the optimization of fuzzy decision trees［J］.Fuzzy Sets and Systems，2000，112（1）：117－125.

［9］ Dubois D.Fuzzy real algebra：some results［J］.Fuzzy Sets and Systems，1979，2（4）：327－348.

［10］ 孙强，张运洲，李隽，等（Sun Qiang，Zhang Yunzhou，Li Jun，et al）.电网规划设计中的风险评估应用（Risk assessment application in power grid planning）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2009，21（6）：17－21，116.