无阻尼LCL滤波器的并网变流器稳定性控制策略

李 军 李玉玲 陈国柱

（浙江大学电气学院 杭州 310027）

1 引言

三相电压型PWM变流器可以实现网侧电流正弦化、功率因数可控及能量双向流动，在电气传动、高电压直流输电、无功补偿和可再生能源并网等领域有广泛的应用前景[1]。为减少变流器开关频率附近的高次谐波，需在变流器和电网之间加入滤波器。在传统的应用中，一般采用单电感滤波，虽然简单、可靠、易于控制，但成本上升，装置体积加大，效率降低，系统动态特性变差。LCL滤波器的引入解决了上述问题，但其在欠阻尼下可能会引起系统谐振，进而可能导致系统不稳定。目前常用两种方式解决此问题：其一是引入无源阻尼[2]，即通过在滤波电容上串联电阻增加系统阻尼来使系统稳定，但其增加了系统的损耗；其二是引入有源阻尼[3,4]，即通过控制算法等效地增加系统阻尼来使系统达到稳定，如超前网络法、虚拟电阻法及基于遗传算法的有源阻尼等。此方法虽然一定程度上降低了系统损耗，但控制比较复杂，需较多的控制参数和传感器，降低了系统的可靠性[5]。根据控制理论可知，连续系统离散化以后，其稳定性可能会发生改变，且不同的采样频率下的离散系统也有不同的稳定性。基于此，本文提出了一种根据电流采样点位置选择合适的采样频率的电流环稳定性控制方法，其不仅不会给系统带来损耗，而且也不改变原系统的控制性能，实现起来简单可靠。仿真和实验结果也有效验证了此方法的可行性。

2 基于LCL滤波器的PWM并网变流器模型

图1是采用LCL滤波器的电压型PWM并网变流器的结构图，其中 L2为 LCL滤波器网侧电感和电网电感的等效值，vsa、vsb、vsc为电网电压，L1为变流器侧电感，C为滤波器电容，R1、R2分别为变流器侧和网侧电感等效电阻。

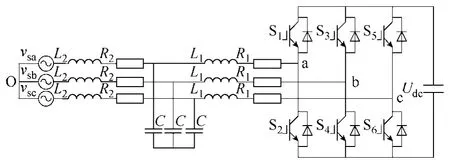
图1 LCL滤波的电压型PWM变流器Fig.1 Voltage-source PWM converter with LCL filter

在基波应用中，基波分量对LCL滤波器而言是低频分量，而LCL滤波器中的电容支路只对高频分量具有低阻通路。因此在确定低频段数学模型时，电容可以忽略，只要在分析系统稳定性时才考虑电容对系统的影响，不考虑电容时dq0旋转坐标系下的三相电压型PWM变流器状态方程如式（1）所示

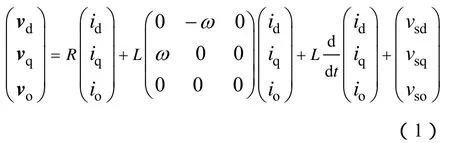
式中，L=L1+L2；R=R1+R2；vd、vq、v0为变流器三相交流输出电压；vsd、vsq、vs0为电网电压，ω=2πf，f为电网频率。在三相平衡系统中三相电流的零序分量为零，因而方程可以简化为

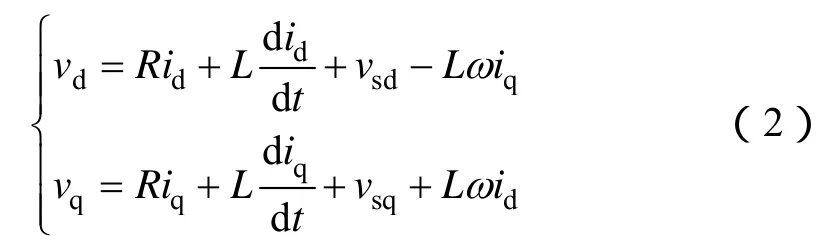
由式（2）可见，d轴、q轴变量相互耦合。为了简化控制器的设计，首先对其前馈解耦，电流环控制框图[6]如图2所示。

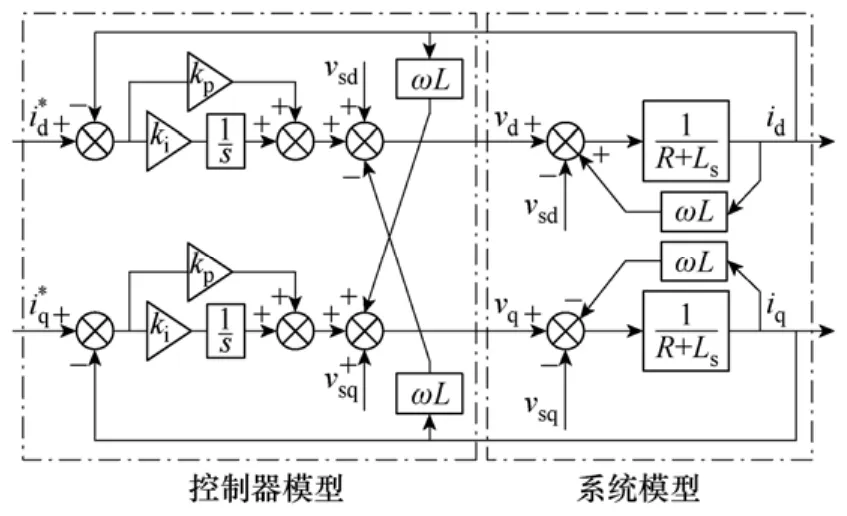
图2 PWM变流器电流环控制框图Fig.2 Current control block diagram of PWM converter

3 电流环稳定性控制策略

在上述数学模型和解耦控制的基础上进行系统稳定性研究，但在进行系统的稳定性设计时，C是不能忽略的，因为电容C的存在使系统存在谐振频率点[7-11]。如果系统不增加阻尼或其他控制措施，电网电压扰动、系统的动态过程、控制器或者传感器噪声等扰动信号都可能触发系统不稳定。本文分别从电网侧和变流器侧两个不同的电流反馈点，系统的研究了采样频率对电流环稳定性的影响，并提出相应的电流环稳定控制策略。

3.1 不同采样频率下的系统稳定性分析

3.1.1 网侧电流反馈

网侧电流反馈控制的结构框图如图 3所示，图中虚线部分是LCL滤波器。

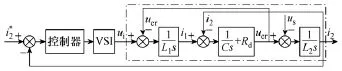
图3 网侧电流反馈控制的结构框图Fig.3 Block diagram of feedback grid current control

网侧电流到逆变器输出电压的传递函数为

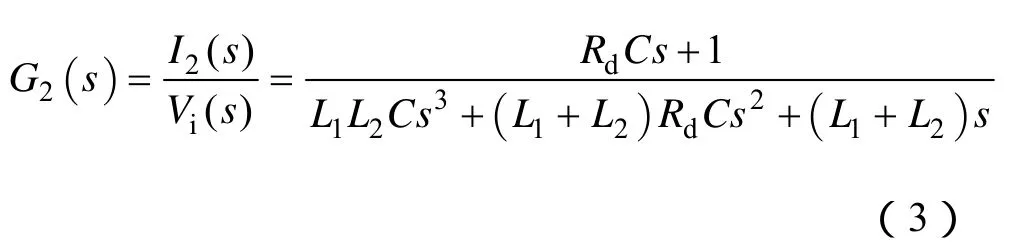
令LCL滤波器参数为L1=0.3mH，L2=0.04mH，C=40μF，Rd=0.018Ω（Rd为电容的寄生电阻），因为其涉及到一个零点，因而不能忽略，文献[12]指出电感的寄生电阻 R1与 R2对系统稳定性的影响可以忽略。LCL滤波器的频率特性如图4所示，由图可见G2(s)存在3个零穿越点，并且在4.24kHz处相频曲线穿越-180°相位，此时对应的幅值增益为23dB，显然在此处通常的相角裕度稳定性判断方法难以适用。实际上，在线性系统频域分析中，奈奎斯特判据是判定系统稳定性的根本方法[11]。由图 5显示在4.24kHz处其超调达到98.9%，阻尼系数只有0.003 51，因而系统闭环不稳定。

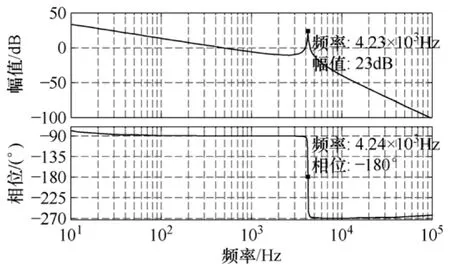
图4 G2(s)的频率特性Fig.4 Bode plot of the transfer function of G2(s)

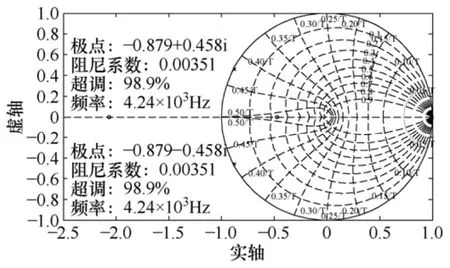
图5 开环零极点分布Fig.5 Zeros and poles of the open-loop transfer function

为了保证系统稳定，需要增加系统阻尼，若引入无源阻尼会增加系统损耗，而有源阻尼一般需要反馈多个变量，参数较多，控制复杂，工程实践中难以实现。

通过观察图4G2(s)的幅频特性可以发现：0.5～4kHz的频率范围内，G2(s)的幅值增益在0dB以下。若增加 G2(s)在这个频段的相移，使-180°相角穿越点在上述频率范围内，则系统可以得到真正的幅值裕度。采用二阶低通滤波器、数字控制的零阶保持器或一拍延时控制都可以产生相移。其中，一拍延时控制的影响尤为明显，而通过采样频率调节延时时间则是一种较简单的控制方式。将式（3）离散化得系统的脉冲传递函数

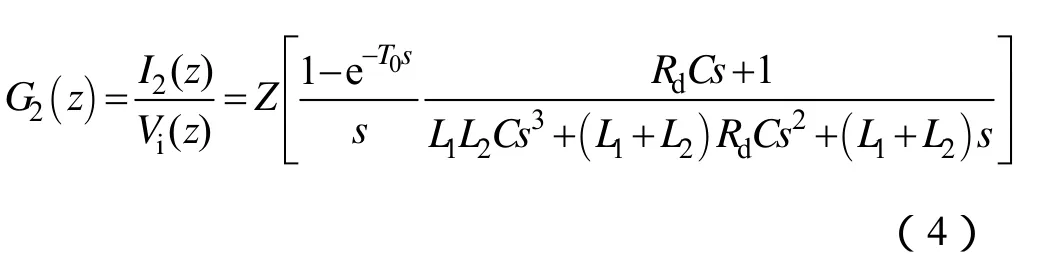
图3控制器用 D(z)表示，则系统的闭环传递函数为

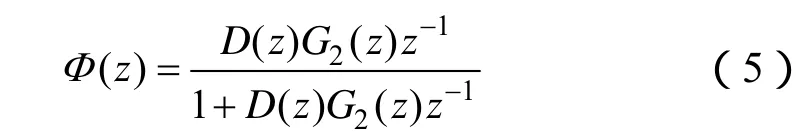
D(z)在这里采用 PI调节器。PI控制器用来增加低频段增益，让其积分引入的相位滞后仅出现在不影响稳定性的低频段，在关系到稳定性的谐振频率处，PI控制器不改变G2(s)的频率特性，z-1是由于计算或检测造成的延时，一般这个延时是一个采样周期，所以又叫一拍延时。取 KP=1，KI=31.47，以上面的PI参数及采样频率由5～20kHz变化时系统的闭环零极点分布，如图6所示。

图6 反馈网侧电流随采样频率变化零极点分布图Fig.6 Zeros and poles of the gird current control varying the sampling frequency from 5 to 20kHz

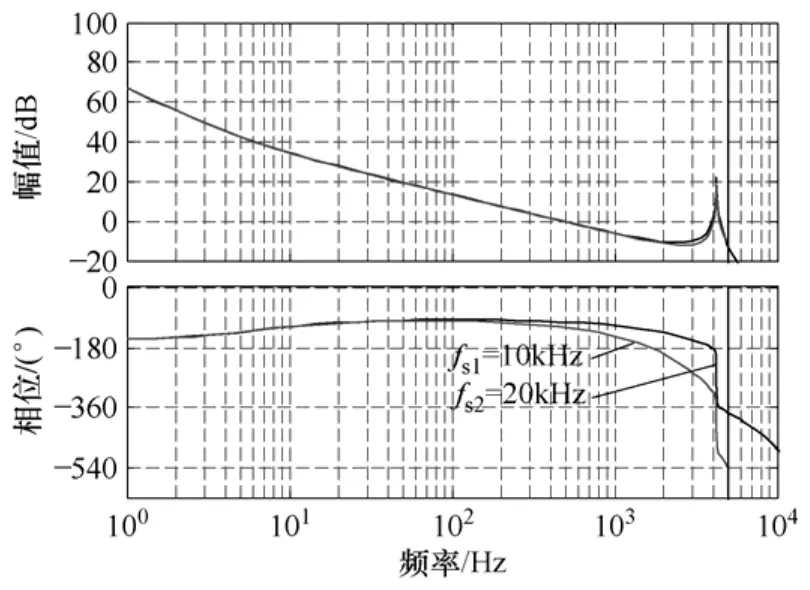
图7 网侧电流反馈开环频率特性Fig.7 Bode plot of feedback grid current control

由图6可见，在本例中，当反馈网侧电流时采样频率在6kHz到接近14kHz时，即引入适当的延时，系统是稳定的；此外的采样频率则不稳定。图中箭头表示主导极点的根轨迹。由根轨迹图可知通过选择合适的采样频率，利用采样延时可使系统稳定。图7为当采样频率分别为10kHz和20kHz时的伯德图，当采样频率为 10kHz时，系统的相频曲线穿越-180°相位穿越点的频率在1.3kHz处，此时的幅值裕度约为9.13dB；而采样频率为20kHz时，相频曲线穿越-180°线的频率在4.2kHz处，此时的幅值裕度为-20dB，此时幅频特性与连续系统相比基本不变，系统不稳定；采样频率为10kHz时的伯德图与图4对比可知延时控制增加了G2(s)在转折频率处的相移，-180°相角穿越从校正前的4.24kHz降为 1.5kHz，而且此时开环奈奎斯特曲线没有包含（-1，0j），系统稳定。

3.1.2 变流器侧电流反馈

图8所示是变流器侧电流反馈控制的控制框图，式（6）是变流器侧电流到变流器输出电压的传递函数。

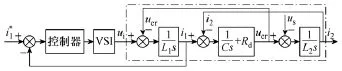
图8 反馈变流器侧电流的控制结构框图Fig.8 Block diagram of feedback converter current control

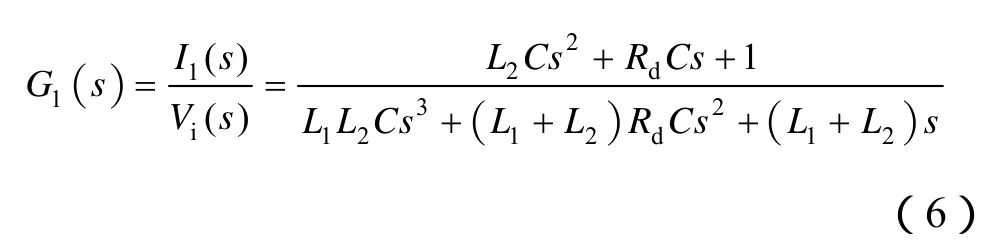
令 LCL滤波器参数 L1=0.3mH，L2=0.04mH，C=40μF，Rd=0.018Ω。G1(s)的根轨迹如图 9所示。无论系统的开环增益K如何变化，系统的闭环极点都不会到达s的右半平面，也就是说此连续系统始终是稳定的。当然K的增大会提高系统带宽，同时把干扰信号也放大，因此K取得过大也没有意义。图9中根轨迹分析是基于模拟系统的，下面研究采样频率对系统稳定性的影响，同样采样频率也在5～20kHz之间变化。将式（6）离散化得变流器侧反馈的脉冲传递函数如式（7）所示。

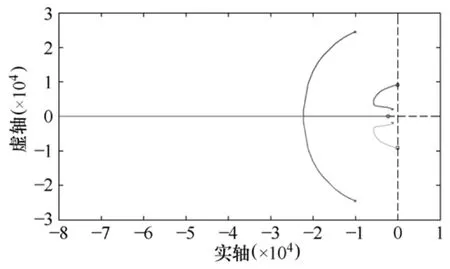
图9 G1(s)的根轨迹Fig.9 Root locus of G1(s)

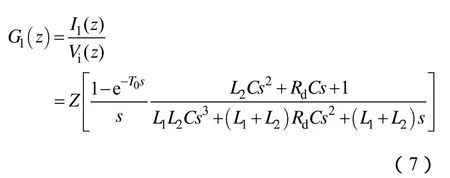
控制器用D(z)表示，则系统的闭环传递函数为

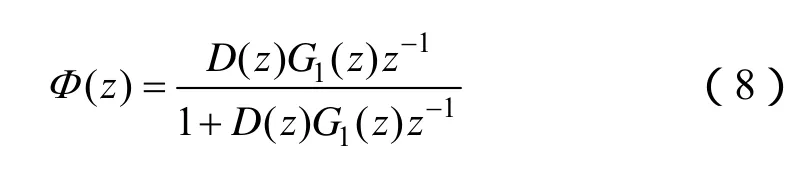
D(z)在这里采用PI调节器，PI调节器的参数取KP=1，KI=31.47，z-1为一拍延时环节。

以上面的PI参数及采样频率由5kHz到20kHz变化时系统的闭环零极点分布，如图10所示。采样频率在5kHz时系统不稳定，当位于6kHz时系统处于临界稳定状态，随着采样频率的增大到系统的阻尼系数越来越大，即系统的相对稳定裕度越大。由此可知采用变流器侧电流反馈时，在连续系统中稳定的系统，离散化后可能变为不稳定。此时可以通过选择合适的采样频率来使系统稳定，而变流器侧电流反馈控制要增加系统的稳定裕度就应该采用尽可能高的采样频率。

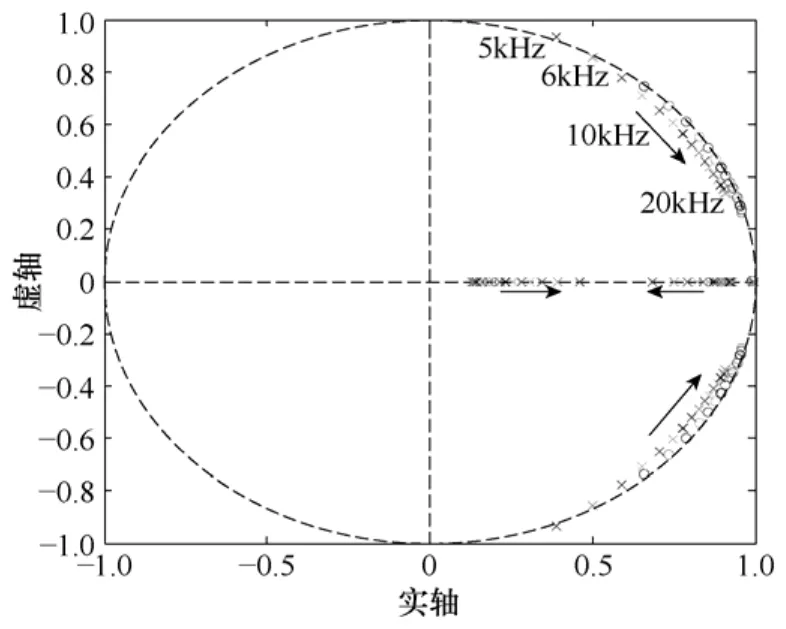
图10 变流器侧电流反馈闭环零极点分布Fig.10 Zeros and poles of the converter current control varying the sampling frequency from 5 to 20 kHz

3.2 采样频率对系统稳定性的影响机理

本节以反馈网侧电流为例分析采样频率对系统稳定性影响的本质。采样频率对系统稳定性的影响是通过延时环节来体现的，除装置本身带来的延时外，一般采样系统中的零阶保持器、二阶低通滤波器都会带来延时，同时也可以人为的加入一拍延时控制。各延迟环节都会使系统的相频特性出现滞后，其中一拍延时带来的滞后最为显著。所以以一拍延时为例来分析采样频率对系统稳定性的影响。图11为考虑延时环节时电流环数字控制框图，其中D(z)是数字控制器的传递函数，G(z)是控制对象的离散传递函数，在这里是指LCL滤波器的传递函数，z-1为一拍延时环节的传递函数。

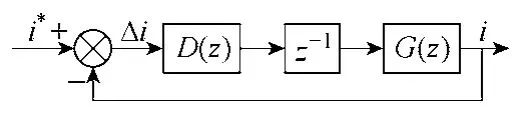
图11 电流环数字控制框图Fig.11 Digital block diagram of current control

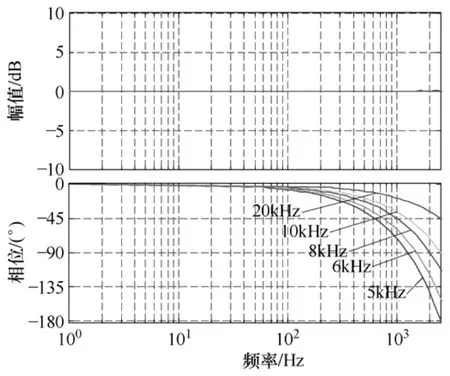
图12 不同采样频率下延时环节z-1的伯德图Fig.12 Bode plot of z-1 in different sampling frequencies

图12是在不同的采样频率下，一拍延时环节的伯德图，可见，一拍延时环节对幅频特性不产生影响，只增加相位滞后，而且在同一频段采样频率越小滞后就越大。这样就可以通过改变采样频率来调节 LCL滤波器中频段的相频特性，从而使系统稳定。而当采样频率到20kHz以上时，其给系统中频段带来的相位滞后较小，对系统稳定性的影响也相对较小。在采样频率对延时环节的影响上，其他延时环节与一拍延时有类似的特性。零阶保持器和二阶低通滤波器虽然在给系统带来的相位滞后上不如一拍延时显著，但二者对系统的高频段有一定的衰减作用，对系统谐振峰可以起到一定的抑制作用，不过并没有将谐振峰值控制在零以下。因此，实际上，往往还是利用相位滞后特性降低了开环相角-180°的穿越频率，利用控制对象中频段的特性提高幅值裕度，使系统稳定。

4 仿真研究

为有效验证以上理论分析的正确性，对系统进行了仿真，仿真参数：L1=300μH，R1=0.05 Ω，L2=40μH，R2=0.02Ω，C=40μF，Rd=0.018 Ω，电网线电压 vs=690V，直流母线电压 Vdc=1200V，开关频率fsw=3kHz。为了体现采样频率对系统稳定性的影响，仿真首先在连续状态下运行，然后在离散状态下采样频率由5kHz变化到20kHz。

4.1 网侧电流反馈控制

图13为网侧电流反馈时各个状态下的网侧电流波形。图13a为连续系统下的波形呈高频振荡，系统不稳定；20kHz时系统振荡如图13b所示；图13c中采样频率为10kHz系统稳定运行。当采样频率为 5kHz系统小幅振荡，闭环系统处于不稳定状态。对比可知仿真结果基本与3.1节图6中的理论分析一致。

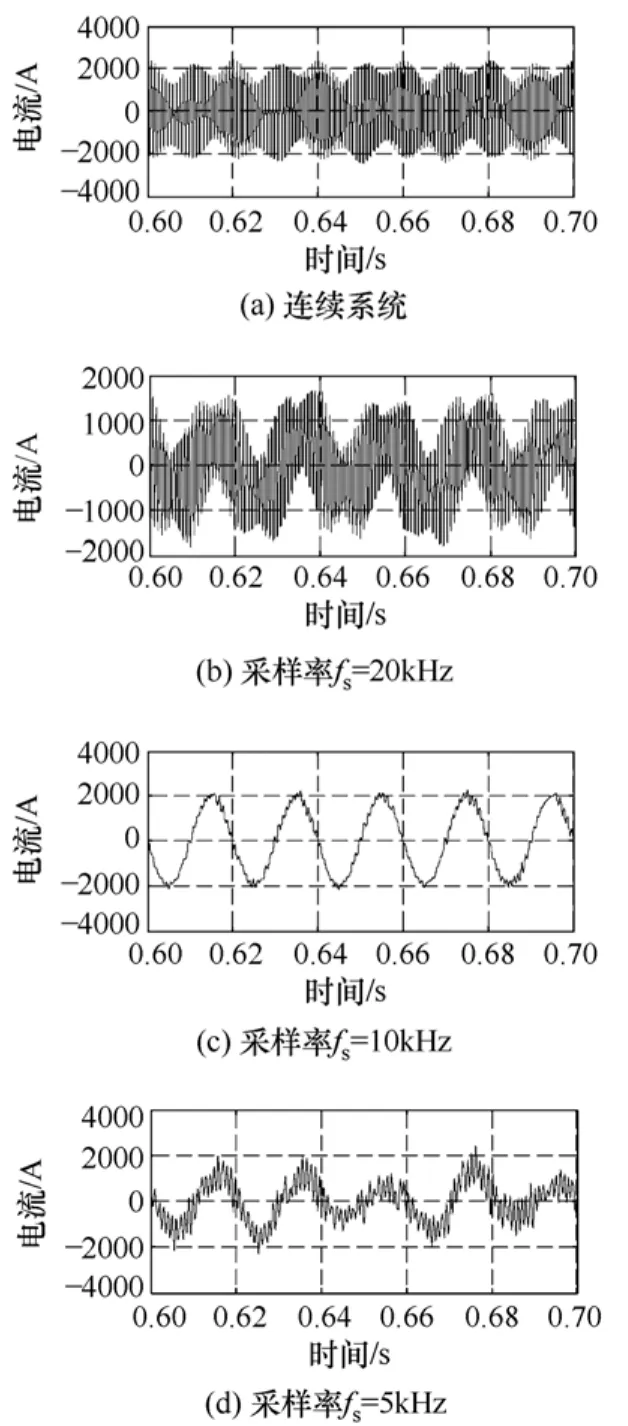
图13 网侧电流反馈仿真波形Fig.13 Simulated grid current of feedback grid current control

4.2 变流器侧电流反馈控制

仿真参数与网侧电流反馈控制时一致，图 14a是连续采样时系统变流器侧电流波形，可见系统在连续状态下是稳定的，这也和理论分析一致，图14b是系统在采样频率fs=10kHz时的仿真波形，可见在10kHz时系统已有一些振荡，说明系统的稳定性在降低。在fs=6kHz时系统已经进入临界稳定状态，如图14c所示，电流波形出现明显振荡。如果继续减小采样频率到fs=5kHz时系统进入不稳定状态，说明在当前参数下系统的采样频率不能低于6kHz，如图14d所示。

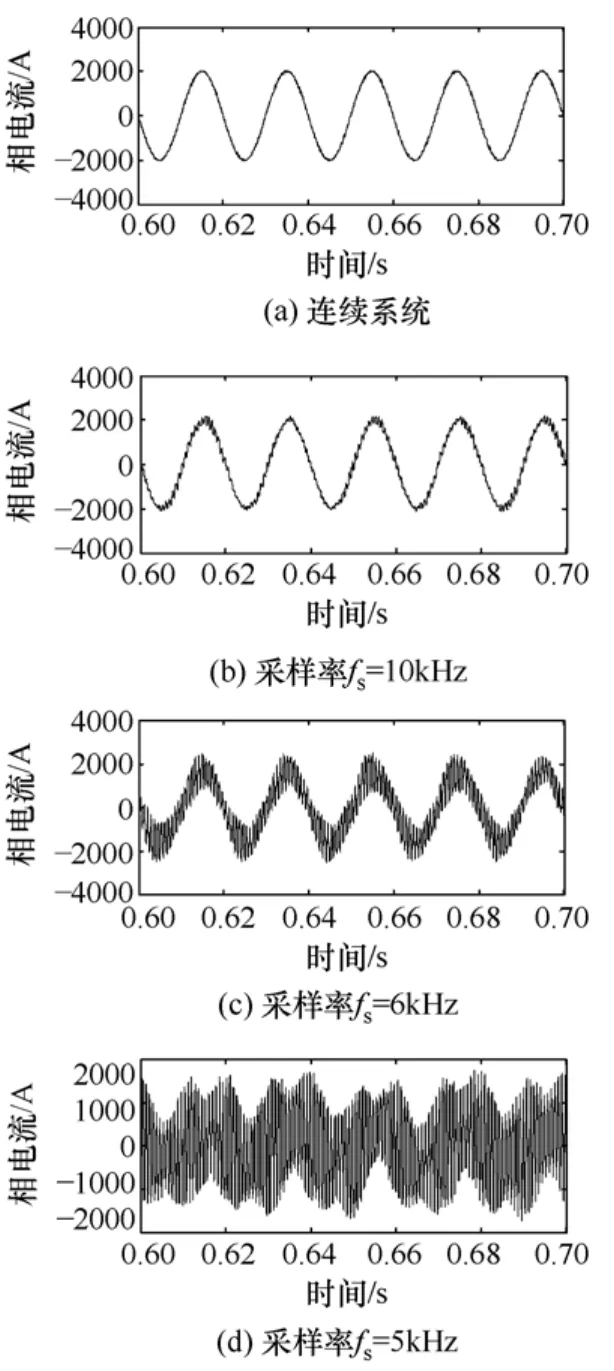
图14 变流器电流反馈仿真波形Fig.14 Simulated converter current of feedback converter current

由上面的仿真和理论分析可知，对于变流器侧电流反馈来说，只要采样频率足够高可以不外加阻尼，系统仍然可以稳定。

5 实验验证

实验参数：L1=3.2mH，R1=0.8Ω，L2=0.3mH，R2=0.05 Ω，C=50μF，Rd=0.018 Ω，电网线电压vs=40V，直流母线电压 Vdc=100V，开关频率fsw=3kHz，同样采样频率由5kHz变化到20kHz。由于做稳定性实验，装置要承受一定的风险，因而实验的参数和功率等级与仿真的不一致，但是其设计理念和控制方法基本是一致的。

5.1 网侧电流反馈

此实验结果与3.1.1节中的理论分析基本一致，即当采用网侧电流反馈时，过高或过低的采样频率系统均不稳定，如图15所示。必须选择合适的采样频率，才能达到利用控制对象的中频段幅频特性提高幅值裕度，使系统稳定。

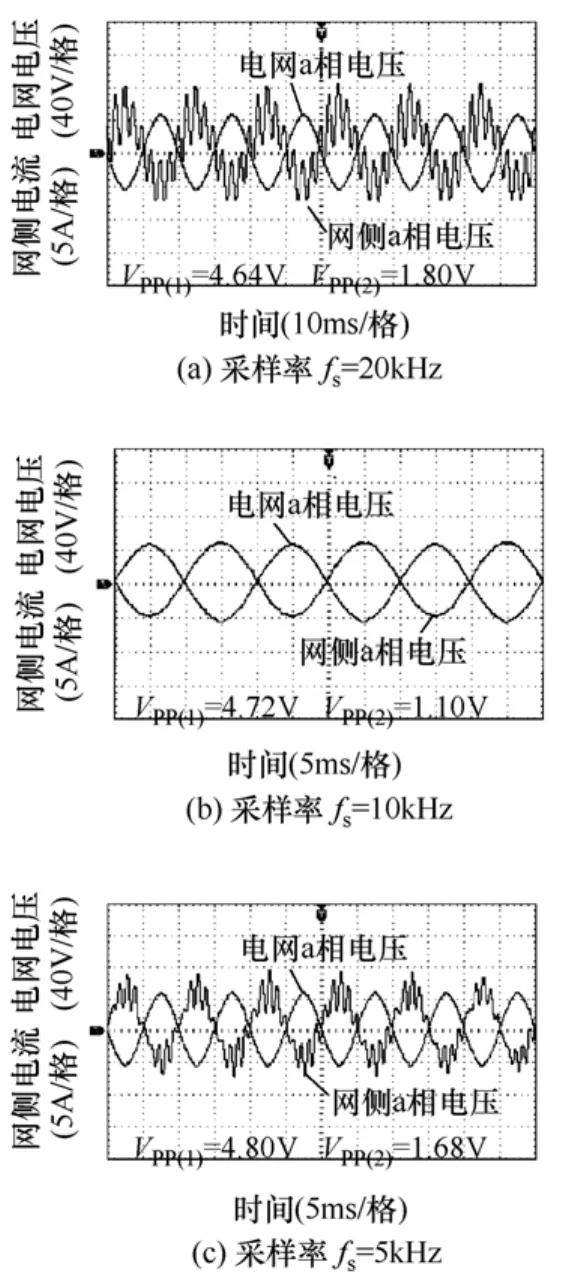
图15 网侧电流反馈实验波形Fig.15 Measured grid-side current of feedback grid current control

5.2 变流器侧电流反馈

由图16可知，实验结果与前文理论分析基本一致。反馈变流器侧电流控制在理论上拥有较好的稳定性，但系统离散化以后，当采样频率过低时系统难以稳定。

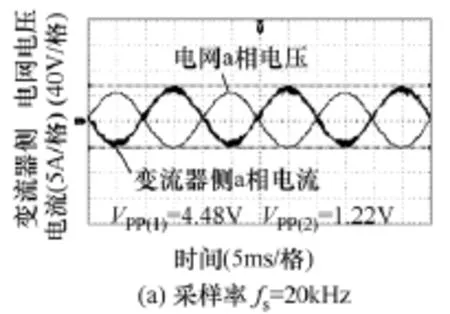
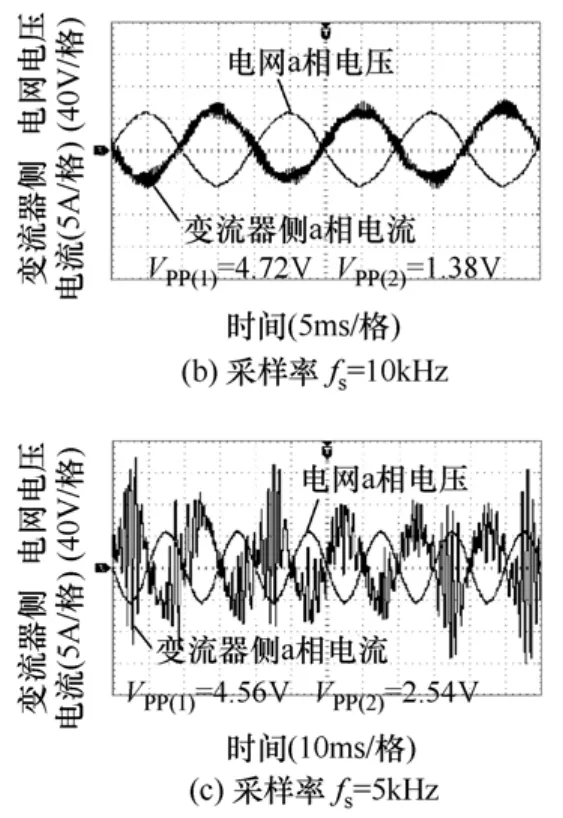
图16 变流器侧电流反馈实验波形Fig.16 Measured converter-side current of feedback converter current control

6 结论

本文对 LCL滤波器的并网变流器采用选择采样频率的稳定控制方法进行理论分析、仿真和实验研究，结果表明：

（1）适当选择数字采样频率，由此有目的地引入适当的延时，可以使LCL并网变流器系统稳定。

（2）稳定采样频率的选择与电流反馈点有关。采用网侧电流反馈时，过高或过低的采样频率都不合适，只有中段频率才能使系统进入稳定。而稳定（或最优采样频率）的选择与控制对象的频率特性、所选的延时控制环节、控制目标和信号带宽等要求有关；当采用变流器侧反馈时，则在允许的范围内，采样频率越高，系统的稳定性越好。

（3）研究表明：采用选择采样频率在改善系统稳定性的同时，对系统的其他性能基本不造成影响。

该方法在系统效率、实现的复杂性和成本等方面均有较大的优势，具有较高的理论与应用价值。

[1]Marco Liserre, Frede Blaabjerg,Steffan Hansen.Design and control of an LCL-filter-based three-phase active rectifier[J]. IEEE Transactions on Power Electronics, 2005, 41(5): 1281-1290.

[2]孙蔚, 伍小杰, 戴鹏, 等. 基于 LCL 滤波器的电压源型PWM整流器控制策略综述[J]. 电工技术学报,2008, 23(1): 90-96.Sun Wei, Wu Xiaojie, Dai peng, et al. An overview of current control strategy for three-phase voltagesource rectifier with LCL-Filter[J]. Transactions of China Electrotechnical Society, 2008, 23(1): 90-96.

[3]张宪平, 林资旭, 李亚西, 等. LCL滤波器的 PWM整流器新型控制策略[J]. 电工技术学报, 2007,22(2): 74-77.Zhang Xianping, Liu Zixu, Li Yaxi, et al. A novel control strategy for PWM rectifier with LCL filter[J].Transactions of China Electrotechnical Society, 2007,22(2): 74-77.

[4]Bierhoff M H, Fuchs F W. Active damping for three-phase PWM rectifiers with high-order line-side filters[J]. IEEE Transactions on Industrial Electronics,2009, 56(2): 371-379.

[5]Rodriguez J, Pontt J, Silva C A, et al. Predictive current control of a voltage source inverter[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1):495-503.

[6]徐德鸿. 电力电子系统建模及控制[M]. 北京: 机械出版社, 2006.

[7]夏德钤, 翁贻方. 自动控制理论[M]. 北京: 机械出版社, 2004.

[8]Malinowski M, Kazmierkowski M P, Szczygiel W, et al. Simple sensorless active damping solution for three-phase PWM rectifier with LCL filter[C]Proceedings of the 31st IEEE Annual Conference of the Industrial Electronics Society, 2005.

[9]Eric Wu, Lehn P W. Digital current control of a voltage source converter with active damping of LCL resonance[J]. IEEE Transactions on Power Electronics.2006, 21(5): 1364-1373.

[10]Kjar S B, Andersen G K. Control aspects of a LCL grid-connected green power inverter[J]. Nordic Workshop on Power and Industrial Electronics. 2002,8: 12-14.

[11]胡寿松. 自动控制原理[M]. 3版. 北京: 国防工业出版社, 1994: 203-209.

[12]仇志凌. 基于LCL滤波器的三线三相并网变流器若干关键技术研究[D]. 浙江大学, 2009.