12脉冲自耦变压整流器的优化与滤波电感的设计

蒋磊磊，陈乾宏，毛 浪

(南京航空航天大学，江苏省新能源发电与电能变换重点实验室，江苏南京210016)

1 引言

对于飞机交流电源系统，机载电子设备采用的大量电力电子器件等非线性元件会对飞机电网造成谐波污染，危害到飞机供电质量和系统的稳定性。民航适航标准RTCA DO-160E和国军标GJB181A-2003均规定网侧电流THD＜10%。多脉冲整流器作为一种无源方案，已在 B787、A380、Arj21等机型上得到了应用［1］。

多脉冲自耦变压整流器按其脉冲数分为12、18、24、30脉冲ATRU，其中在相同输出功率条件下12脉冲自耦变压整流器的等效容量最小，体积重量占有优势，受到航空领域的青睐。但12脉冲自耦变压整流器输入电流 THD理论计算值为15.2%［2］，不满足航空标准。现有的减小输入电流THD方法有谐波注入和交直流侧串入电感两种方法。其中谐波注入方法在降低系统可靠性的同时会引入高频干扰因此并不为人们所接受。本文即采用了在交直流侧串入电感的方法减小输入电流的 THD，同时通过理论分析给出交直流侧电感的计算方法。针对三相不控整流电路，各种谐波分析方法相继被提出。如考虑直流侧的电感为有限值，输出电流有脉动分量，而忽略交流侧电感引起的换相过程，这种情况下可以采用Dobbinson法来对脉动电流近似处理，其核心思想是将两个正弦波顶上各60°的波头部分，叠加在方波上，近似代表直流侧电流脉动的情况［3］;在Dobbinson法的基础上，考虑交流侧电感引起的换相过程，并近似认为换相过程中电流线性变化，这就是 Graham-Schonholzer法［4］。在直流侧电流脉动为中等或严重的情况下，这两种方法的精度已经较高，特别是Graham-Schonho lzer法的误差比较小，已被列入国际标准IEEE519-1992所建议的谐波分析方法中。以上两种分析方法都只针对单组三相整流电路，本文采用 Graham-Schonholzer的分析方法，对12脉冲整流电路在非理想情况下输入电流谐波进行分析，为交直流电感的设计提供理论依据。

2 非理想条件下P型12脉冲自耦变压整流电路的谐波分析

12脉冲自耦变压器采用P(Polygon)型结构，主电路结构如图1所示，Ls为各相交流侧电感，Ld为直流侧电感，Co为输出电容。限于文章篇幅，具体电路分析和工作原理见参考文献［2］。将图1中输出电流的脉动部分用正弦波的波头来近似，同时考虑交流侧电感引起的换相过程。

设换相重叠角为γ，12脉冲自耦变压整流电路整流桥输入电流ia'，如图2所示，四个正弦波头叠加在120°+γ的梯形波上，梯形波的斜边是对换相过程的近似。

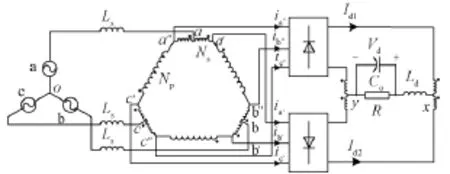
图1 P型12脉冲自耦变压整流器Fig.1 P type 12-pulse auto-transformer rectifier

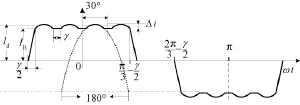
图2 12脉冲整流电路电流ia'近似波形Fig.2 Waveform of ia'in 12pulse auto-transformer rectifier

IB为换相末电流，Δi为电流波头脉动的峰峰值，引入电流纹波比rB来表示电流脉动的程度:

图2所示的电流波形可以用IB、rB和换相重叠角γ这三个变量表示。对电流波形进行傅里叶分解，可得基波和各次谐波的统一表达式，其中n=1或n=6k±1，k为整数，In表达式为:

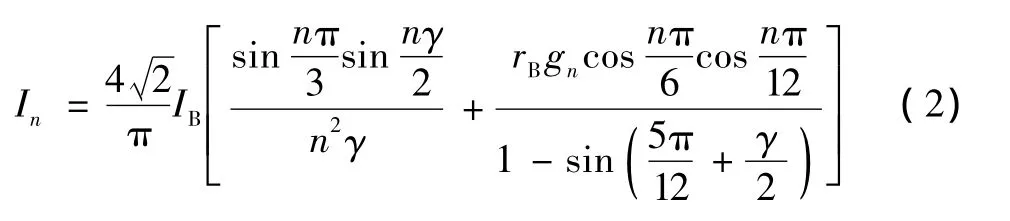
其中，gn的表达式为:

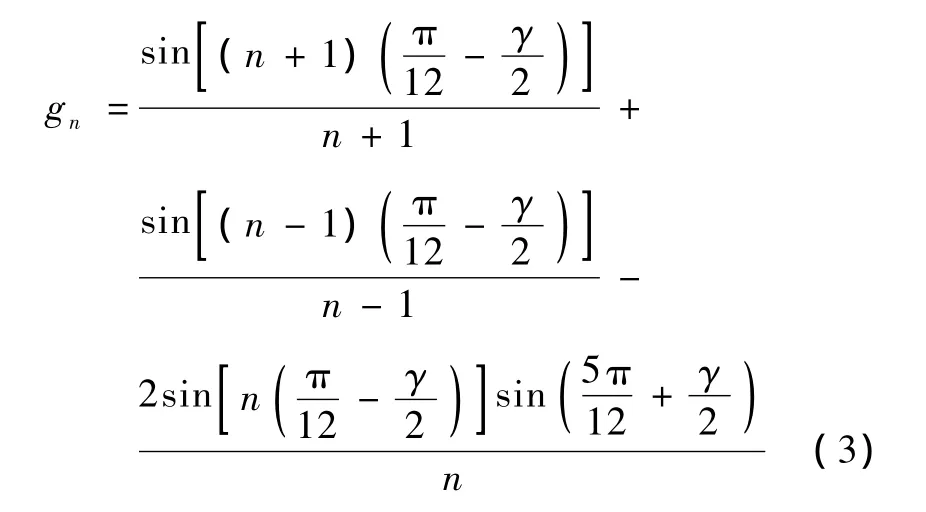
根据文献［2］对P型12脉冲自耦变压整流电路的原理分析，交流侧输入电流为

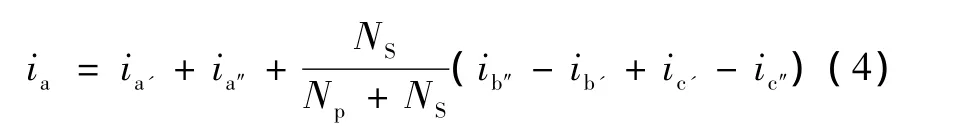
已知电流ia'表达式，根据各电流间相位关系，可得到交流侧输入电流ia的傅里叶分解表达式为

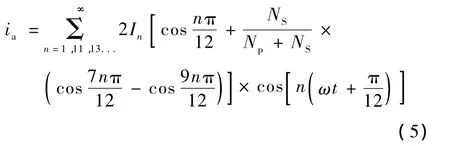
其中，n=1或n=12k±1，k为整数。从式(5)可以看出，交流侧输入电流中已不含有5次、7次谐波。

不同电流纹波比和移相重叠角下输入电流THD如图3所示。在电流纹波较小时，随着移相重叠角的增大，输入电流 THD减小。相反，电流纹波比大于一定值，移相重叠角增大，THD增大。

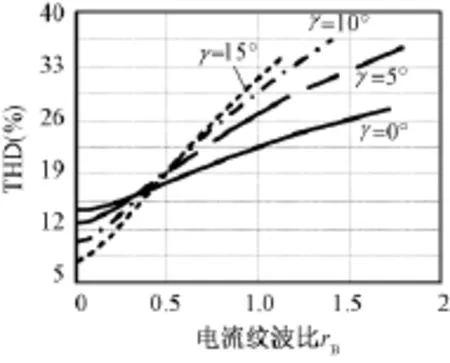
图3 电流纹波比和输入电流的THD关系曲线Fig.3 Curve of current ripple and THD

3 系统设计

本文设计了一台4kW P型12脉冲自耦变压整流器，系统指标见表1。

表1 系统指标Tab.1 System parameter

3.1 交直流电感值的设计

3.1.1 交流侧电感的设计

12脉冲整流电路的两组整流桥互相独立工作，因此计算换相重叠角时可以只考虑其中一组整流电路换相的情况，ωt=0时c'相电流开始向a'相转换，则换相过程应满足如下方程:

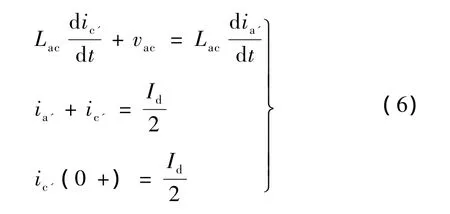
求解可得电流ia'表达式为:

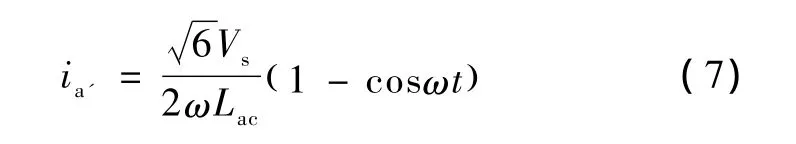
式中，Vs是输入电源相电压的有效值。当ia'=Id/2时，换相结束，因此换相重叠角为:

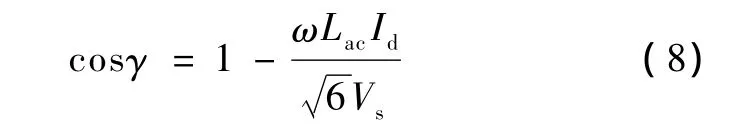
系统指标要求满载情况下输入电流THD＜10%，12脉冲输入电流的 THD=15.2%，因此必须引入直流电感和交流电感进一步减小THD。由图3曲线，此处取换相重叠角γ=15°，电流纹波比rB=0.2。根据式(8)可得交流侧电感的大小:

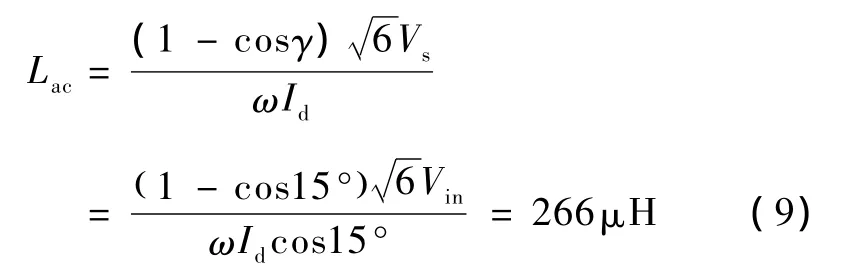
3.1.2 直流侧电感的设计

通过计算加在电感上的电压在一个脉波内的积分，可以求出电流纹波［5］。根据12脉冲自耦变压整流器工作原理可知，由于平衡电抗器的作用整流桥中每个二极管导通120°，平衡电抗器中点电压如图4中虚线所示，12脉冲自耦变压整流器的输出电压为270V，因此可得直流侧电感上的压降见图5。图中阴影部分即为直流侧电感承受的正向电压。

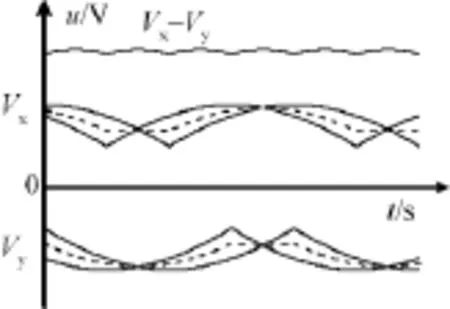
图4 12脉冲自耦变压整流器各点电压波形Fig.4 Voltagewaveforms in 12-pulse ATRU

由 rB=0.2 和式(1)得，IB=13.92A，Δi=3.48A。由 U =Ldi/dt得，所需直流侧电感量为130μH。

3.2 磁性元件的设计

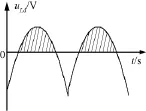
图5 直流电感电压波形Fig.5 Voltage waveform on DC inductor

在400Hz这种中频场合中硅钢带因其价格低廉是最被广泛应用的磁芯材料。其饱和磁密为1.6T，考虑损耗取其最大工作磁密为1.2T。但航空领域中对系统体积重量的要求非常高，因此有必要找到一种饱和磁密更高的磁芯材料以减小磁性元件的体积重量。铁钴钒材料也适合工作在中频场合，其饱和磁密为2.4T，考虑损耗取其最大工作磁密为2.0T。但铁钴钒材料在制作过程中需经过特殊的热处理工艺，因此价格比较昂贵。

本文先后采用了硅钢片和铁钴钒完成了自耦变压器及电感的设计，并进行了比较，见表2。由设计结果证明了由于铁钴钒材料的饱和磁密相对硅钢片较高，因此铁钴钒材料的磁性元件在体积重量上有很好的优势如图6和图7所示。

图6 硅钢片与铁钴钒变压器Fig.6 Silicon steel and Fe-Co-V transformers

图7 硅钢片与铁钴钒电感Fig.7 Silicon steel and Fe-Co-V inductors

4 实验结果与讨论

实际实验中由于变压器存在漏感，交流侧电感取220μH，直流侧电感取130μH。图8所示为整流桥一相的输入电流，从波形可以看出此处电流并非理想条件下的矩形波，而是具有换相重叠角和电流脉动的波形，与前文提出的近似电流波形相近。图9所示为系统的三相输入电流波形，输入电流波形为12脉波组成的近似正弦波，通过功率分析仪测得输入电流的THD仅为9%，满足指标要求。

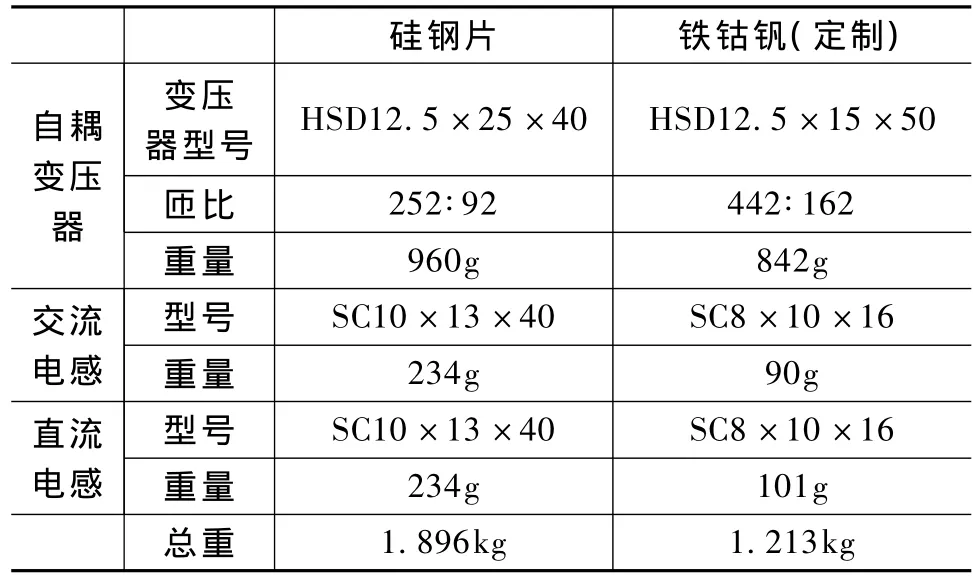
表2 硅钢片与铁钴钒磁性元件参数Tab.2 Silicon steel and Fe-Co-V magnetic components’parameter

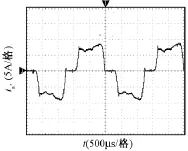
图8 整流桥一相输入电流Fig.8 One phase input current of rectifier

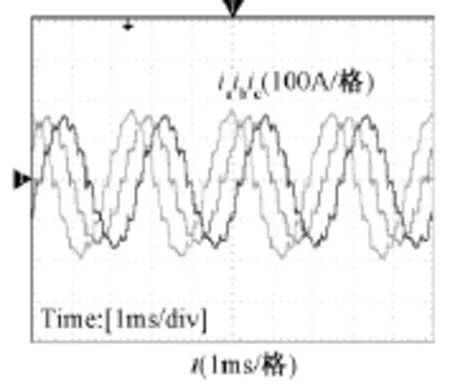
图9 系统三相输入电流Fig.9 Three-phase input current

图10为12脉冲自耦变压整流器的效率曲线，系统满载情况下效率大于95%，满足要求。图11为输入电流的THD随输出功率变化的曲线，在重载情况下，均能保证输入电流的THD小于10%，同样满足指标要求。图12为输入电流的基波及各次谐波电流值，其谐波主要含量为12k±1次谐波。

5 结论

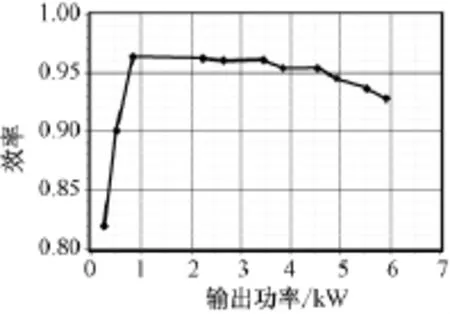
图10 系统效率曲线Fig.10 System efficiency curve

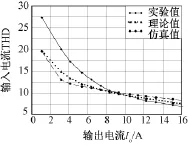
图11 输入电流THD曲线图Fig.11 Input current THD curve

图12 输入电流各次谐波的电流值Fig.12 Value of harmonic current

本文考虑换相重叠角和直流侧电流脉动，分析了P型12脉冲整流电路的输入电流谐波。基于分析结果，本文研制了一台4kW 12脉冲自耦变压整流器，并采用交流侧和直流侧加入电感滤波方案将输入电流THD降低至10%以下，实验结果也证明负载较大时，谐波分析结果与实验结果吻合较好。同时本文还针对这一系统分别制作了硅钢片与铁钴钒两种材料的系统，并对两个系统的体积重量进行比较，结果表明由于铁钴钒的饱和磁密较大，有效地减小了系统的体积重量。

［1］陈伟 (Chen Wei).多电飞机供电系统研究 (The investigation of more electric aircraft power system)［A］.中国航空学会航空电气工程第六届学术年会论文集(The 6thAnnual Conference of Chinese Aviation Institute Aviation Electrical Engineering)［C］.2005.

［2］任志新(Ren Zhixin).多脉冲自耦变压整流器(ATRU)的研究 (The investigation of multi-pulse ATRU)［D］.南京:南京航空航天大学 (Nanjing:Nanjing University of Aeronautics and Astronautics)，2008.

［3］Dobinson L G.Closer accord on harmonics［J］.Electronics and Power，1975，21:567-572.

［4］Graham A David，Schonholzer Emil T.Line harmonics of converters with DC-Motor loads［J］.IEEE Transactions on Industry Applications，1983，19:84-93.

［5］Schaefer J.Rectifier circuits:theory and design［M］.New York:John Wiley＆ Sons，1965.