基于概率谐波电流源的交流电力机车模型研究

田钰笙，姜齐荣，田 旭

(清华大学电机工程与应用电子技术系，北京100084)

1 引言

近年来，采用交-直-交传动系统的动车组列车已成为多条客运专线的主要牵引负荷，其电气性能与交-直型机车有较大差异，有必要对其合理建模以分析机车负荷对电力系统造成的影响。电力机车的模型可以分为主电路模型和等效电流源模型。主电路模型包含整个牵引传动系统，即整流桥、逆变器和牵引电机。该模型可以较准确地得到机车负载的工频特性，但在谐波特性方面却可能与实际负荷存在一定差距。原因主要有:①动车组内部电气参数控制方法未公开，同时补偿装置的运行状态也难以获得;②受线路条件、天气等因素的影响，机车负荷的谐波具有随机波动性;③牵引网的影响会使得某些谐波放大或衰减，流入牵引变电所的谐波电流和机车注入牵引网的谐波电流并不一致［1］。

本文提出了一种交流电力机车的概率谐波电流源模型，将机车负载等效为一个接在变电站牵引变压器副边的电流源。其基波分量由带有等效直流负载的四象限整流桥得到，谐波部分则采用符合实际分布规律的概率谐波电流源。采用概率统计法分析牵引负荷谐波特性在国内外研究中已有许多应用并且取得了很好的效果［2-5］。本文采用一种改进的最大熵法，基于大量实测数据分析了机车负荷主要谐波的概率密度函数，并在 PSCAD仿真平台上利用MATLAB接口模块实现了相应的概率谐波电流源模型。模型可同时用于仿真机车负荷的冲击性、负序以及谐波对电力系统的影响。由于电流源模型的谐波分量直接利用实测数据，因此谐波仿真结果更接近实际情况。

2 机车负荷谐波分布特点

本文采用的数据来自郑西线某牵引变电站，数据记录时长为1天。实验数据显示:

(1)机车负荷谐波主要集中在 3、5、7、9、19、21、23、25、27、39、45 等奇次频率上;

(2)谐波的相角在四个象限内分布均匀;

(3)谐波分布规律和基波电流大小相关，当基波电流较小时，谐波分布特征有较大变化。

以3次谐波为例，在不同基波电流大小情况下谐波散点图分布如图1所示，图中所有数据均取自非空载工况下的实验数据(认为基波电流大于30A为非空载工况)，相角以基波电流为参考相量。

3 机车负荷概率谐波分析

3.1 数据预处理

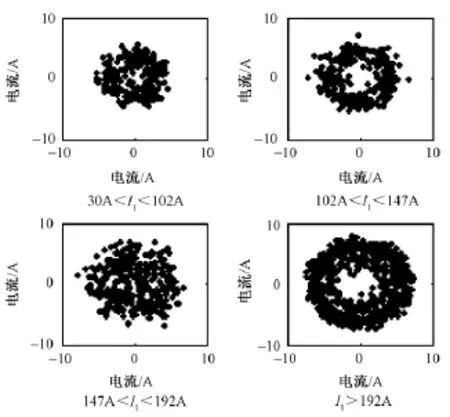
图1 3次谐波电流散点图Fig.1 Scatter diagram of 3rdharmonic current

(1)牵引变电站采用AT供电方式，实测数据为接触线和馈线各次谐波的幅值和相位。利用磁势平衡原理可以通过接触线和馈线的电流计算出自耦变压器原边电流。以自耦变压器原边作为等效电流源的接入点，可以略去馈线电流的建模。

(2)电力机车概率谐波模型仅考虑线路带有负载的情况，已将实验结果中空载情况下的数据滤除。按照基波电流大小对谐波电流数据分组，分别进行概率密度函数估计。

(3)谐波电流的幅值和相位均具有随机波动性，在直角坐标系下，谐波电流可以看做X坐标分量和Y坐标分量的叠加。本文关于概率密度函数的估计建立在直角坐标系下，并且为了简化分析，假定这两个分量相互独立，可以分别进行统计。

3.2 概率密度函数获取

目前常用的概率密度函数估计方法有最大熵法和最佳平方逼近法，二者都具有简明的解析表达式且估计精度较高。本文提出了一种改进的最大熵法，提高了最大熵法的估计精度和效率，并与最佳平方逼近法的估计效果加以比较，最终选择最大熵法作为实验数据处理方法。

3.2.1 最大熵法

最大熵原理由 E.T.Jaynes于 1957年提出，其主要思想是在只掌握关于未知分布的部分知识时，应该选取符合这些知识但熵值最大的概率分布［6］。

信息论中把随机变量X的熵定义为:

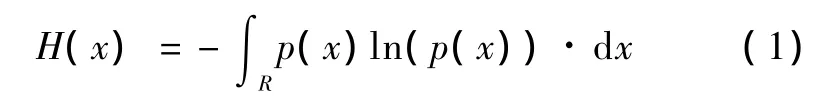
其中，p(x)是随机变量X在取值x处的概率密度;R是随机变量X的定义域。于是概率密度函数估计转化为如下的优化问题:

显然，m0=1。

选择l阶原点矩，构造如下的拉格朗日方程:

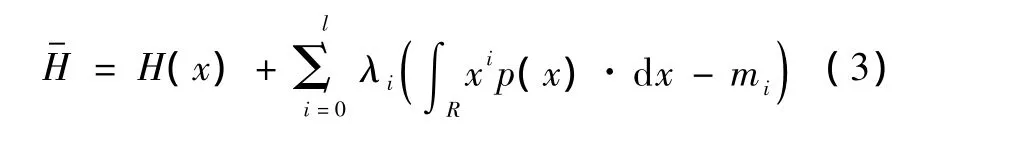
根据拉格朗日方程极值条件 ∂H－/∂p(x)=0可以得到最大熵概率密度函数的解析表达式:

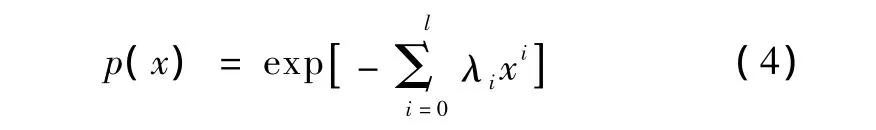
相应的 λ0，λ1，λ2…λl满足的非线性方程为:

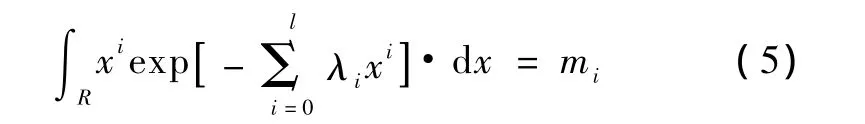
一般取较低阶矩(4～5阶)就能取得很好的估计效果。

3.2.2 最佳平方逼近法

最佳平方逼近法的思想是用n次多项式对有限的实验数据构成的概率密度分布进行最小二乘拟合。通过MATLAB的相关函数可以验证该方法的估计结果能够自然满足各阶矩的约束条件。由于最佳平方逼近法并不是本文论述的重点，相关内容可参考文献［3］，本文不另作介绍。

3.2.3 改进的最大熵法

实验数据是随机变量的离散取值。假设N是对统计数据按随机变量大小进行等间隔分组的组数，xn是第n组对应的数据点，Δx是数据点之间的间隔，是根据每组的样本数量计算得到的xn处概率密度，是根据式(4)计算得到的xn处概率密度，则式(5)对应的离散数据方程为:

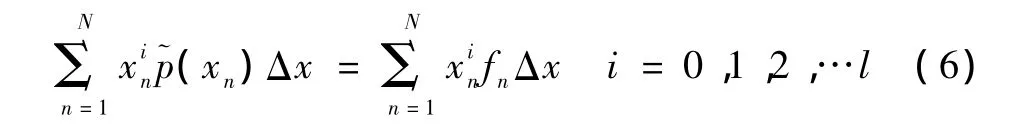
通常采用迭代法对式(6)对应的l+1个非线性方程进行拉格朗日系数 λ0，λ1，λ2...λl的求解［6］，但这种方法初值选取不当就很容易造成求解时间过长，甚至出现找不到合适解的情况。考虑到最佳平方逼近法可以自然满足各阶矩的约束条件，本文对最大熵法的求解过程加以改进，保留其概率密度表达式，但是将拉格朗日系数的约束条件转为如下的最小二乘拟合问题:

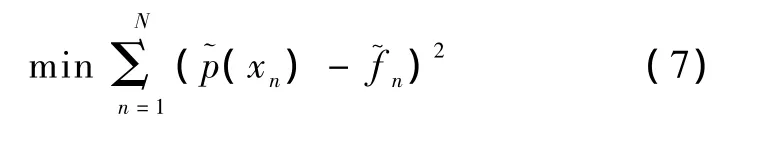
即通过使用最小二乘拟合来满足阶矩约束条件。本文选用4阶最大熵法估计，将概率密度估计结果代入式(6)等号左右两边分别计算，每一阶矩的相对误差均在1e-3数量级以下。

3.2.4 三种方法估计精度比较

选取波形和实际谐波分布情况类似的两种分布:正态分布、双峰分布(由两个正态分布构成)对三种估计方法进行验证，评估指标为均方差指标(Mean Squared Error，MSE)，计算公式为:

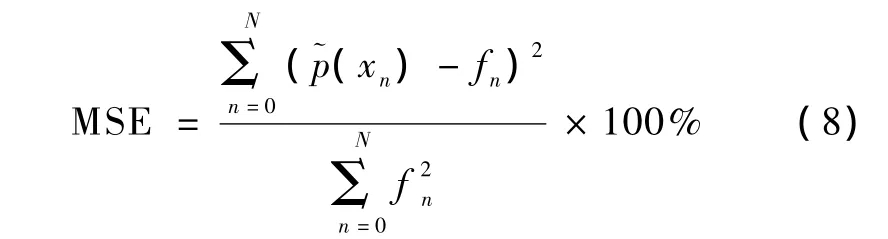
其中，fn是将xn代入实际分布函数表达式计算得到的实际概率密度。最大熵法选择4阶估计，最佳平方逼近法选择9阶估计。非线性函数求解选择MATLAB中fsolve函数，最小二乘拟合选择 Isqnonlin函数。针对每种分布进行50次实验，取平均值作为最终的估计精度，结果见表1。

表1 正态分布和双峰分布三种方法估计精度Tab.1 Estimation results on normal distribution and double-peak distribution using three methods

实测数据样本容量在200～1000之间，比较结果显示，在此范围内，对于单峰分布和双峰分布，改进的最大熵法估计精度均为最高。

3.3 主要特征谐波概率密度函数估计结果

以3次和25次谐波为例，在基波电流I1＞192A情况下的概率密度函数估计结果如图 2和图 3所示。

对于双峰分布的情形，在两峰连接处截断，分别对两峰进行概率密度函数估计。在连接处可能会出现不连续的情形，但由于最终利用的是分布函数(参见4.1节)，即概率密度函数积分的结果，所以一处不连续的点对最终结果没有影响。

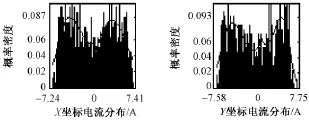
图2 3次谐波电流随机分量概率密度函数估计结果Fig.2 Estimation results of random vector of 3rdharmonic

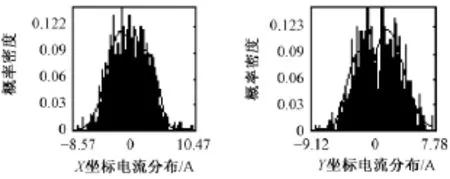
图3 25次谐波电流随机分量概率密度函数估计结果Fig.3 Estimation results of random vector of 25thharmonic

4 基于概率谐波电流源的电力机车模型

4.1 概率谐波电流源在PSCAD中的实现

可以证明，若随机变量X服从概率密度为p(x)的分布，则随机变量 F(X)服从［0，1］区间上的均匀分布，其中 F(x)为随机变量 X的分布函数［7］。按照上述方法，建立不同基波电流大小情况下各主要谐波含量的分布函数数据表，通过生成［0，1］上均匀分布的随机数查找表中对应的随机变量值，就能产生符合实际分布规律的各次谐波X轴分量和Y轴分量，进而得到各次谐波的幅值和相对于基波电流的相位。在PSCAD中引入MATLAB接口模块可以随机生成符合实际分布规律的各次谐波幅值和相位。

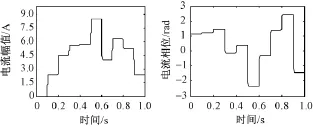
图4 3次谐波电流幅值和相位刷新波形Fig.4 Amplitude and phase update waveform of 3rdharmonic

图4是3次谐波电流的幅值和相位刷新波形。如果仿真时间足够长，谐波电流幅值和相位的仿真数据的分布规律将与实测数据的分布规律相符。考虑到谐波的X坐标分量与Y坐标分量并不是完全独立，且概率密度函数估计本身存在误差，仿真和实测数据的分布规律会存在一定偏差，但统计结果显示(参见第5节)该偏差很小。

4.2 基于概率谐波电流源的电力机车模型

电力机车的概率谐波电流源模型如图5所示。牵引供电臂一侧接有负载，另一侧空载。图5中，TA、TB、TC为牵引变电所高压侧进线，iload为四象限整流桥模型在自耦变压器原边产生的电流，idiff为电流修正量，iload_n为修正之后的机车负载电流。

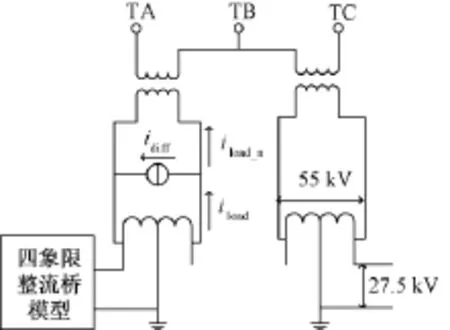
图5 基于概率谐波电流源的电力机车模型Fig.5 Locomotive model based on probabilistic harmonic current source

假设计算得到的谐波电流为 ih，通过锁相和傅里叶分析得到 iload中基波分量瞬时值为 iload_1，则电流的修正量idiff的计算表达式为:

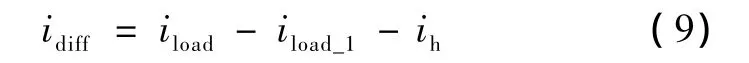
修正之后的负载电流iload_n为:

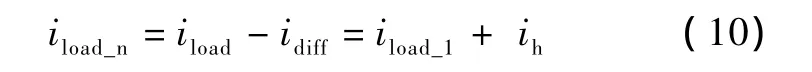
其基波分量为四象限整流桥模型的基波电流，谐波分量由随机电流源模型产生。

5 模型仿真结果

根据线路机车型号，选择三电平四象限整流桥，主电路参数选择参考文献［8］:牵引变压器容量17.6MVA(考虑到有上行和下行同时带有负载的情况)，额定电压27.5kV/1.5kV，折合到二次侧漏感L=0.2mH，电阻R=0.02mΩ，直流侧支撑电容C1=C2=80mF，直流侧电压 Ud=3kV，载波频率1250Hz。

牵引和制动工况下接触网与馈线之间的电压差uTF以及机车负荷电流iload_n的仿真波形如图6所示，为了便于观察，将电流波形放大了100倍。波形显示，四象限整流桥的功率因数控制效果良好。通过整流桥搭建的物理模型可以较好地仿真机车负荷的冲击性以及负序对电网的影响。

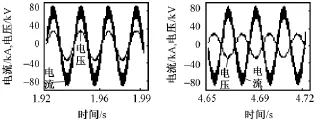
图6 牵引和制动工况下的机车负荷电流以及接触网馈线电压差仿真波形Fig.6 Simulation curve of load current and catenaryfeeder voltage on traction condition and braking condition

概率谐波ih的仿真结果如图 7所示，可以看出仿真得到的谐波电流具有随机波动性。

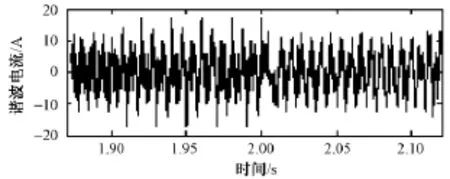
图7 概率谐波ih仿真结果Fig.7 Simulation curve of probabilistic harmonic current

为了验证模型谐波的仿真效果，按照实测机车功率分布情况对机车模型的负载功率进行设定，得到1000组谐波电流仿真数据。变电站牵引变压器副边各次谐波95%概率值的仿真值与实测数据统计结果如图 8所示。可以看出模型谐波大小仿真结果非常接近实际情况。谐波相角的分布接近均匀分布，此处不再列出仿真结果。

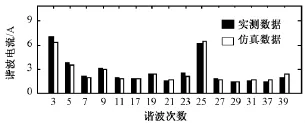
图8 谐波电流95%概率值仿真结果和实测数据比较Fig.8 Comparison of 95%harmonic value of simulation result and measured data

6 结论

本文基于大量实测数据，使用改进的最大熵法分析了某牵引变电所机车负荷的谐波分布特征，考虑了负荷谐波受基波电流大小以及路况等随机因素的影响，利用 PSCAD的 MATLAB接口模块实现了电力机车概率谐波电流源。用带有等效直流负载的三电平四象限整流桥模拟机车负荷的基波电流，叠加上概率谐波电流源就得到了机车负荷的等效电流源模型。由于概率谐波电流源基于实测数据，避免了牵引网以及机车电气参数和控制策略等因素对谐波仿真结果的影响，因此更接近实际情况。该模型可同时用于仿真机车负荷的冲击性、负序以及谐波对电网的影响。本文提出的基于概率谐波的交流机车建模方法对于其他类型的牵引负荷也是适用的。

［1］郎兵，吴命利 (Lang Bing，Wu Mingli).牵引网谐波模型及其仿真计算 (Harmonics model of traction network and its simulation)［J］.电力系统自动化 (Automation of Electric Power Systems)，2009，33(17):76-80.

［2］杨少兵，吴命利 (Yang Shaobing，Wu Mingli).基于实测数据的高速动车组谐波分布特性与概率模型研究(Study on harmonic distribution characteristics and probability model of high speed EMU based on measured data)［J］.铁道学报 (Journal of the China Railway Society)，2010，32(3):33-38.

［3］解绍锋，李群湛，赵丽平 (Xie Shaofeng，Li Qunzhan，Zhao Liping).电气化铁道牵引负载谐波分布特征与概率模型研究(Study on harmonic distribution characteristic and probability model of the traction load of electrified railway)［J］.中国电机工程学报(Proceedings of the CSEE)，2005，25(16):79-83.

［4］韩奕，李建华，黄石柱，等 (Han Yi，Li Jianhua，Huang Shizhu，et al.).SS4型电力机车的动态模型及随机谐波电流计算 (Dynamic model and computation of probabilistic harmonic currents for type-SS4 locomotive)［J］.电力系统自动化 (Automation of Electric Power Systems)，2001，25(4):31-36.

［5］Morrison R E，Clark A D.Probabilistic representation of harmonic currents in AC traction systems［J］.IEE Proceedings on Electric Power Applications，1984，131(5):181-189.

［6］徐俊 (Xu Jun).基于信息熵原理的电气化铁道概率谐波研究 (The study of probabilistic harmonics electrical railway based on maximum entropy method)［D］.上海:上海交通大学(Shanghai:Shanghai Jiaotong University)，2009.

［7］叶俊，赵衡秀 (Ye Jun，Zhao Hengxiu).概率论与数理统计 (Probability and Mathematical Statistics)［M］.北京:清华大学出版社 (Beijing:Tsinghua University Press)，2005.

［8］邓学寿 (Deng Xueshou).CRH2型200 km/h动车组牵引传动系统 (Traction drive system of 200km/h CRH2 EMUs)［J］.机车电传动(Electric Drive for Locomotives)，2008，(4):1-7.