扩散项与时滞有关的单种群模型的全局稳定性

李晓艳，姚 频

(兰州城市学院 a.数学学院;b.附中，兰州 730070)

用数学模型的方法来研究种群生态学问题是常见的方法，具有扩散的种群模型的周期解问题的结论较多，而具有时滞的单种群扩散模型中扩散项仅依赖于当时种群的密度是不完全符合现实的。

在自然界中，许多生物体(尤其是植物)必须经历一段时间才能发生扩散;举例来说，柳树、松树要迁移，必须靠风的力量，由风传播它们的种子才能生根发芽;麻雀在出生后不能立即展翅飞翔，要经过一段时间后才能飞，这是发生扩散的基本条件。因此，为了更符合客观事实，应考虑扩散项具有时滞的模型。

1 模型建立

考虑如下非自治单种群模型

其中:ai(t)是内禀增长率;bi(t)为密度制约因子;Ci(t)为繁殖率;Di(t)(i=1，2)是扩散率;τ 是关于t 的函数且τi(t)(i=1，2，3)是连续的ω 周期函数，且ai(t)，bi(t)，Ci(t)，Di(t)均大于0，τi(t)≥0，τ˙i(t)＜1，t≥0。

2 周期解的存在唯一性与稳定性

定理1 设系统(1)满足如下假设

则系统(1)的任一正解均一致有界。

证明:由假设(A1)必存在r ＞1，H ＞1，使得

定义:V ( x1，x2)=max { x1，x2}，下面分2 种情况

可见“醉鬼”不醉，只是以醉态示人。至于为何如此，有人说是他藏形隐色，掩饰真功以防暗算的一种做法；有人说是他为了免除权贵骚扰，故意所作的玩物丧志饮酒误事的假象。

(1)若V ( x1，x2)= x1，沿 系 统(1)的 正 解 计 算 的 右 导 数，若‖ (x1(t)，x2(t))‖ ≥H，则 对 任 意θ ∈ [ -τ，0 ]，有V (x1( t+θ )，x2( t+θ ))＜rV (x1(t)，x2(t))。由( 1 )得

(2)若V ( x1，x2)=x2，同理可得·V＜-1。由Lyapunov 稳定性定理知，正解是最终一致有界的。

设M ＞H ＞1，(x1(t)，x2(t))表示具有初始条件 ( σ，φ )的任意正解，φ = ( φ1，φ2)∈C+。当θ∈ [ -τ，0 ]时，有0≤φi( θ )≤M，( i=1，2 ).下证对t≥σ，都有‖ (x1(t)，x2(t))‖≤M。

假设存在¯t ＞σ，使得

若

则

由(4)和(5)得

引理1［4］设条件 ( A1)成立，则存在正数ε ( 0 ＜ε ＜M )，使得对给定的0 ＜δ ＜d，总存在正数T = T ( δ，d )＞0，使得对任意t ＞σ+T(σ∈R，φ∈C+[ δ，d ])有xi( σ，φ )≥ε。

证明:令 (x1(t)，x2(t))是系统( 1 )的正解，作变换Xi(t)=ln ( xi(t ))，i=1，2，则系统( 1 )转化为关于X1，X2的新系统。由定理1与引理1 可知，新系统的解也一致有界，由定理4.2［5］得新系统至少存在一个不动点，即至少存在一个正ω 周期解，从而系统( 1 )至少存在一个正ω 周期解。

令σi(t)=t-τi(t)，则σi(t)有反函数，记作ui(t)=max {Di(t)t∈R，i=1，2 }。

定理3 对系统(1) ，若满足以下假设

其中i，j=1，2，i≠j，ε 和M 分别为系统(1) 的任意正解的最终下界和上界，则系统(1) 存在唯一全局渐进稳定的正ω 周期解。

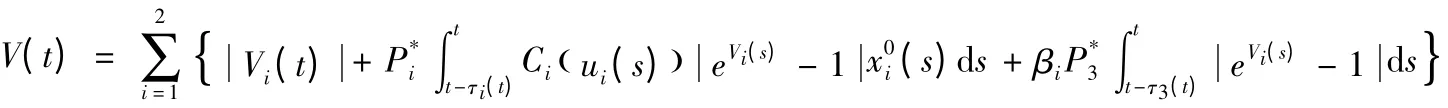
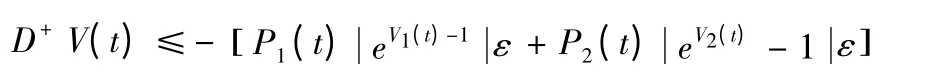
由假设(A2)得D+V(t)≤0，所以系统(1)的周期解是全局渐近稳定的。

同时文献［7］的模型是bij(t)=cij(t)=0 时的特殊情况。

［1］Wang H，Zhang S.Permanence and Existence of Periodic Solutions of a Predator-Prey Patchy Model with Dispersal and Time Delay［J］.Journal of Biomathematics，2007，22(1):25-36.

［2］陈超，纪昆.具有Holling III 类功能性反应的多种群捕食竞争系统的周期解［J］.应用数学学报，2006，29(4):756-765.

［3］韩思远，贾建文.具有时滞和扩散的基于比例的捕食系统的正概周期解［J］.陕西师范大学学报，2008，4(21):18-21.

［4］Wang C，Pei Y. Global Stability for a Single-Species Plant Model with Delay in Diffusion［J］. Journal of Biomathematics，2005，20:129-134.

［5］Hale J.Theory of Functional Differential Equations［M］.Heidelberg:Spinger Verage，1977.

［6］陆征一，周义仓.数学生物学进展［M］.北京:科学出版社，2006.

［7］马知恩.种群生态学的数学建模与研究［M］.合肥:安徽教育出版社，2000.

［8］马知恩，周义仓.常微分方程定性与稳定性方法［M］.北京:科学出版社，2001.