PBX 细观损伤特征及表征方法研究综述

郭 虎，罗景润，谢朝阳

(中国工程物理研究院 总体工程研究所，四川 绵阳 621900)

高聚物粘结炸药(PBX)是由主体炸药颗粒和高聚物粘接剂等组成的固体高能炸药。PBX 是一种颗粒高度填充复合材料，图1 是PBX 典型的细观结构，主要由形状不规则的炸药颗粒和粘结剂组成，炸药颗粒的尺寸在几十到几百微米之间，图2 是其中炸药颗粒边界形貌，左上方和左下方是较大的炸药颗粒边缘，夹在其中的是较小的炸药颗粒和粘结剂。PBX 的颗粒填充度高达85%以上，且炸药晶体和高聚物粘结剂的性能差异很大，这使得PBX 不同于传统的颗粒填充式复合材料，有一些特殊的力学性能。

从大量细观观测和力学实验结果可以看出，PBX 是一种含初始损伤的脆性材料。在外加载荷的作用下，这些损伤会进一步演化，以颗粒断裂、界面脱粘、粘接剂基体开裂、变形孪晶以及剪切带等形式使炸药的力学性能劣化，使结构的强度和刚度下降。在持续的载荷作用下，各种形式的损伤会进一步生长、聚合，形成宏观裂纹，最终导致材料破坏［1-2］。同时，PBX 是一种含能材料，其起爆机理(特别是XDT)与炸药的损伤有密切的联系。

图1 PBX 典型细观结构［32］

PBX 的安全性日益受到关注，含损伤的本构模型是其研究的基础，而如何对PBX 的损伤进行表征并应用于本构模型中是研究的重要内容。目前，国内外对于PBX 损伤的表征方法已经有不少研究，但是大都只适用于某个本构模型或者某种特定的加载条件，还没有比较通用的有物理基础的表征方式。本文将PBX 损伤的表征方式分为经验型和物理型进行了归纳与总结。

图2 炸药颗粒边界形貌［3］

1 PBX 细观损伤特征

1.1 初始损伤特征

PBX 由主体炸药颗粒和一定的粘结剂组成，PBX 的初始损伤受单相材料本身和成型工艺的影响。图3 显示了PBX9501 的初始细观损伤，其中含有大量方向随机、尺寸不一的缺陷，主要是大颗粒的内裂纹和孪晶带，这些缺陷主要来自于PBX 的压制成型过程，同时，炸药颗粒中与颗粒间的孔隙也是PBX 初始损伤的重要部分。受合成和结晶过程的影响，在炸药晶体内部会有孔穴及气泡等初始缺陷［4］。造型粉是由粘结剂将若干炸药颗粒简单粘结而成，比较疏松，在炸药颗粒之间有很多孔洞，而且有的炸药颗粒表面光滑，没有粘结剂，表明粘结剂并未完全包覆某些炸药颗粒。

图3 PBX 初始细观损伤［8］

一般情况下，粘结剂的模量很低，要比炸药晶体的模量低几个量级，压制成型后粘结于晶体的边界。Palmer 等［3］用原子力显微镜(AFM)对HMX 基的PBX 进行观察，得到粘结剂的相位图像(图4)，主要由三部分组成:a)表面上鹅卵石形状的结构，长50 ～100 nm，有的似乎已经断裂，b)平坦的区域和c)比较暗的小区域。对这些结构的解释有很多，比较合理的是，鹅卵石状结构是很小的炸药晶体，平坦区域是大块的粘结剂而较暗的区域可能是较软的粘结剂。

图4 粘接剂的相位图像［3］

压制成型是PBX 一种重要的成型方法，可分为热压和冷压两种。实验表明［5］，热压成型中，压制压力为50MPa 时(PBXN-5)，晶粒之间有较多的孔洞，但没有明显的颗粒破碎;压制压力为100 MPa 时(PBXN-5)，发现晶粒之间孔洞减少，而在一些炸药晶体中产生了微裂纹;压制压力为200 MPa 时(PBX9404)，发现微裂纹增多，而且可以清楚地看到孪晶带。可见，随着压制压力的增大，损伤程度也会增加。实验表明［6-7］，炸药颗粒的平均粒径随着压力的增加而减小，且冷压过程中颗粒的破碎比热压过程中颗粒破碎严重，常温下压制的PBX 药柱的密度明显低于高温压制样品的密度。

因此，PBX 是含初始损伤的材料，其初始损伤主要来自压制成型过程，主要表现为炸药颗粒的内裂纹、孪晶带和颗粒中与颗粒间的孔隙。

1.2 损伤演化特征

在外加载荷的作用下，PBX 的细观损伤会发生演化，且演化机制或者说形式会因加载方式的不同而有所不同，有时甚至会表现出明显的差异。

拉伸与压缩的加载条件下，PBX 的损伤形式有很明显的区别。一般用对径压缩实验对准静态拉伸状态下损伤的演化进行研究［8-12］，实验发现，微裂纹通常在大颗粒的边界首先形成，这些微裂纹随载荷增加逐渐生长并贯通，最后裂纹进一步扩展直至材料破坏。断口观察表明，界面脱粘和粘结剂开裂是拉伸状态下最主要的破坏形式，而穿晶断裂则较少发生，图5 显示了界面脱粘和粘结剂开裂的现象，可以看到裂纹路径上粘结剂被拉伸为纤维状，而有的地方已经发生脱粘。罗景润［13］从断裂力学的角度分析，由炸药晶体(-HMX 的断裂韧性计算得到它发生破坏的最小应力，并将其与PBX9501(HMX 平均粒径150 μm)拉伸破坏应力的实验值相比较，结果发现后者比前者小得多，也得到穿晶断裂较少发生的结论。与拉伸状态不同，PBX 在压缩状态下的主要破坏形式为穿晶断裂。Skidmore 等［14］和Trumel等［16］分别对以TATB 和HMX 为基的PBX 进行准静态单轴压缩实验，发现大量方向随机的微裂纹，主要是晶内裂纹，有些裂纹甚至贯穿了炸药颗粒，它们主要来自大颗粒晶体间的相互挤压，局部区域的微裂纹会发生聚合，最终产生宏观裂纹导致材料断裂。另外，随着压力的增加，炸药颗粒会产生塑性变形，并以平行的变形带出现，也就是孪晶带。可见，PBX 在压缩状态下的损伤与初始损伤相似，只是随着压缩的压力的增大，损伤程度更加严重，其原因在于压制成型过程本身就是一定程度的压缩加载过程。

图5 拉伸状态下的界面脱粘与粘结剂开裂［8］

在动态压缩的条件下［14-15］，PBX 的损伤演化现象与静态压缩大致相同。但是，动态压缩下，有大量的微裂纹聚合发生，而且微裂纹在局部区域表现出一定的方向性，如图6 所示。在压缩蠕变的情况下［34］，微裂纹主要出现在炸药晶体的边界处。

Trumel 等［16］对约束应力下PBX 的细观损伤演化进行了研究。在不同应力水平(20 ～800 MPa)的三轴约束应力下，对HMX 基的PBX 进行准静态、动态压缩和热循环等试验，发现约束应力有减少微裂纹密度和阻止微裂纹聚合的作用，而晶体颗粒的塑性会增加，并在晶体中发现了屈曲现象。

热载荷也是常见的加载方式，李敬明等［33］对TATB 基的PBX 进行热循环刺激，出现了样品体积的膨胀，膨胀速率随循环次数的增加而放缓。Willey 等［34］对LX-17 进行了热循环实验，发现体积的膨胀中有一部分是不可逆的，并称之为棘轮增长(ratchet growth)，主要来自于炸药晶体热膨胀的各向异性。细观观察表明，热循环后PBX 的损伤主要是炸药晶体内的孔隙和裂纹。另外，文献［18，35-37］对PBX 在“热冲击”下的损伤进行了一定的实验研究，“热冲击”就是将样品快速地从较低温度移到较高温度的环境中，产生温度的突变。实验表明，“热冲击”下主要产生晶内裂纹，损伤的程度随温度差的增大而加剧，而且存在一个临界的温度差，小于临界值时样品内损伤的程度基本没有变化。

综合以上结果，PBX 细观损伤的演化在各种加载方式下有明显的差异。拉伸状态下主要是界面脱粘和粘结剂开裂;准静态压缩下主要是晶内裂纹和孪晶带，而动态压缩下，裂纹在局部区域会有一定的方向性;热载荷作用下主要出现晶内裂纹。

图6 动态压缩下有方向性的微裂纹［16］

2 PBX 损伤表征方法

2.1 经验型表征方法

对于PBX 的损伤的测量包括直接测量和间接测量，直接测量方法包括显微观察、超声波、声发射、X 射线、小角中子散射等，间接测量方法包括测量密度、体积、弹性模量和泊松比等［1］。其中，超声波、声发射等测量结果常用于PBX 损伤的表征。

超声波测量是通过测量损伤前后声阻抗的变化来评价损伤［15，17］。可以利用声速变化、幅值衰减以及频率的变化等来表征损伤的变化情况，通过声速变化来定义损伤是一种常用的方法。可以定义损伤度如下:

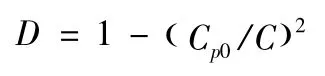
该表征方法将宏观参量与细观损伤联系起来，形式简洁，测量方便，但是其损伤度只是相对值，而且缺少对细观损伤特征的描述。测量时，超声波对炸药的损伤也会有一定的影响。

声发射(AE)技术是通过对损伤(微裂纹、孔洞等)演化过程中释放的弹性应力波的鉴别来探测损伤的位置、类别及其演化［13，18-19］。该技术能得到加载过程中声发射信号幅值、事件数、振铃计数、能量累积、能量变化率等随时间的变化情况，然后定性地分析出损伤的起始、扩展直至断裂的演化过程和损伤的破坏模式。通过声发射能量定义损伤，还可以获得损伤度的演化。

另外，用高能X 射线和膨胀计等技术测得的结果(孔隙率等)也可以对炸药的损伤进行一定程度的表征。

基于实验测量结果的表征方法能在一些方面反应出PBX 的损伤特征，并能给出一些定量的结果，但是，由于PBX 损伤的复杂性，该方法尚不够完善和准确。

PBX 炸药的损伤与应变、应变率等因素密切相关，周风华等［20］研究高应变率下有机玻璃非线性粘弹性本构模型时，考虑到微裂纹等损伤的演化的不可逆性以及损伤在客观上起到的弱化作用，定义了包含损伤演化阈值的损伤内变量D:

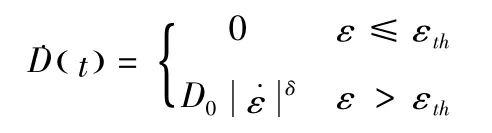
其中D0，δ均为材料常数为损伤演化的应变阈值，损伤内变量0≤D≤1，D =0 时表示无损伤，D =1 时表示完全丧失承载能力。

李英雷等［21］在对TATB 钝感炸药本构关系的研究中，借用了以上对损伤内变量的定义，并根据TATB 钝感炸药的损伤情况进行了一定的修正。通过对实验数据和样品的细观分析，确认了TATB 炸药属于含初始损伤的非线性粘弹性体，也就是材料一开始承载就有损伤裂纹发展，因此=0，并定义损伤内变量D:

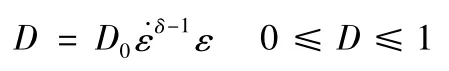
将该损伤变量应用于ZWT 本构模型中，能较好地描述TATB 炸药在102～103s-1应变率下的动态压缩行为。但是它只能唯象地描述损伤的变化，并没有反应出材料的物理特征。

2.2 物理型表征方法

采用连续损伤力学或细观损伤力学进行研究时，首先要选择一个或多个基准的量来定义损伤变量。一般可以作为基准的量分为两类:宏观的基准(模量、强度、密度等)和细观的基准(孔隙的数量、形状、取向等)。

1)对于宏观的基准，一般总是采用那些对所研究的损伤过程比较敏感，在实验室易于探测的量，作为定义损伤变量的依据。罗景润等［22］在研究简单拉伸下PBX 的损伤时，认为微裂纹与微孔洞是随机分布的，从而假设其损伤是各向同性的，然后用单位面积的微缺陷密度来定义材料的损伤。

对于一维问题，损伤变量D 定义为:

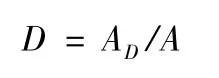
式中A 为试件的横截面表观面积，AD是试件横截面上经应力集中和缺陷相互作用修正后的缺陷痕迹群的总面积，也就是说AD不仅包含横截面上微裂纹、微空洞等缺陷的面积，还计及了应力集中与微缺陷的相互作用。

由于PBX 属于脆性材料，其断裂韧性很低，因此损伤变量的取值范围如下:

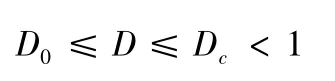
式中:D0为材料的初始损伤;Dc为损伤的临界值。

如果将试件横截面上的各种缺陷等价为均匀分布的微裂纹，可得:

由此可得到PBX 材料的初始损伤为:

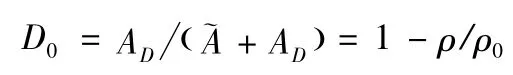
另外，由应变等效性原理还能得到该损伤变量与有效弹性模量~E 的关系:

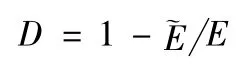
并把确定损伤的这种方法称为弹性模量下降法。

这种通过面积比定义的损伤，形式简洁，有明确的物理意义，结合弹性理论可以较好地描述PBX 材料试件在拉伸载荷下的力学行为。但是，该损伤的定义基于材料的损伤各向同性的的假设，并不适用于各向异性的情况，给其应用带来一定的局限。

2)对于细观的基准，不能直接与宏观的力学量建立本构关系，所以在用它来定义损伤变量的时候，需要对它做出一定的宏观尺度下的统计处理(平均，求和等)。

1985年，Dienes［23］提出针对含损伤的脆性材料的统计裂纹力学模型(Statistical Crack Mechanics，SCRAM)。该模型［24，25］应用应变率叠加原理，将不同类型的损伤结合起来，推导出控制方程，并将其简化为只含有一个自由参数的三阶微分方程。

SCRAM 模型考虑了损伤材料内部的各种力学行为对应变率的影响，包括弹性变形、塑性变形、裂纹张开、闭合裂纹的剪切变形、裂纹生长和粘性变形等。材料总的应变率表示为各部分叠加求和，并将裂纹分为稳定剪切、不稳定剪切、闭合剪切、稳定张开和不稳定张开等状态进行分析。

SCRAM 模型可以应用于大变形的情况，而且在分析中考虑了裂纹的方向，可以应用于各向异性材料。但是，由于SCRAM模型比较复杂，实际应用中进行了一定的简化和改进［26-28］，建立了ISO-SCRAM 模型和Visco-SCRAM 模型等。

Bennett 等［26］在分析PBX9501 的冲击点火中采用了粘弹性各向同性微裂纹损伤模型Visco-SCRAM。该模型由一个广义Maxwell 结构表示的粘弹性体和一个微裂纹损伤体串联而成，应用Addessio 等［28］的研究结果，将微裂纹损伤体的开裂偏应变与偏应力的关系表示为:

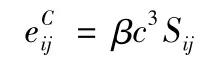
式中:β 为与剪切模量和初始裂纹尺寸相关的参数;c 为微裂纹平均半径。

可以看出，该简化模型中主要用微裂纹尺寸等参数来表征材料的损伤，如果要考虑应变率，还会涉及到微裂纹扩展速率。

SCRAM 模型以材料的细观损伤为基础，用微裂纹平均尺寸等统计参数来表征材料的损伤，与前述的表征方法相比，有更明确的物理基础，同时也增加了该方法的复杂性，如所需参数较多，而微裂纹扩展速率等参数难以测量等。所以，该表征方法需要进行适当的完善和简化［29-31］，才能得到较好的应用，这将是PBX 力学行为研究领域的一个重要发展方向。

4 结论与展望

PBX 是一种含初始损伤的材料。初始损伤主要来自于压制成型过程，主要表现为炸药颗粒的内裂纹、孪晶带和孔隙等损伤形式，其损伤的程度主要受到成型工艺的影响，包括压制压力、温度等。

受到加载方式的影响，PBX 损伤的演化特征表现出明显的差异。在拉伸状态下，主要的损伤形式是界面脱粘和粘结剂开裂;在静态压缩状态下，是晶内裂纹和孪晶带，而动态压缩下，裂纹会有一定的方向性;热载荷作用下，是晶体内部的裂纹。值得注意的是，PBX 的压制过程同时也是压缩加载的过程，所以PBX的初始损伤与压缩加载后的损伤特征相似。

目前，PBX 细观损伤的表征方法可以分为经验型和物理型两种。经验型的表征方法形式简单，便于应用到本构模型中，但是缺乏对物理过程的分析;而宏观的物理型方法利用易于测量的宏观物理量来定义损伤变量，形式简洁，同时也有一定的物理基础，但是采用了各向同性的均匀化假设，有一定的局限性;细观的物理型表征方法分析了细观损伤演化过程，利用微裂纹尺寸等细观物理量来表征损伤，有明确的物理基础，但是形式比较复杂，需要确定的参数较多，需要经过一定的简化才能得到较好的应用。综上所述，基于细观损伤的表征方法将是PBX 力学行为研究领域的一个重要方向。

［1］陈鹏万，黄风雷.含能材料损伤理论及应用［M］.北京:北京理工大学出版社，2006.

［2］Palmer S J P，Field J E，Huntley J M.Deformation，strengths and strains to failure of polymer bonded explosives［J］.Proc R Soc Lond A，1993，440:399-419.

［3］W.G.Proud，S.J.P Palmer，J.E.Field，et al.AFM studies of PBX systems［J］.Thermochimica Acta，384(1 -2)，2002:245-251.

［4］Palmer S J P，Field J E. The deformation and fracture of β-HMX［J］. Proc R Soc Lond A，1982，383:399-407.

［5］C. B Skidmore，D. S Phillips，et al. The Evolution of Microstructural Changes in Pressed HMX Explosives［C］. In:11th International Detonation Symposium，1998.

［6］梁华琼，雍炼，唐常良.RDX 为基的PBX 炸药压制过程损伤形成研究［J］.含能材料，2009，17(6):713-716.

［7］庞海燕，李明，温茂萍，等.温度对PBX 炸药压制的作用［J］.兵器材料科学与工程，2011，34(1):21-23.

［8］Rae P J，Goldrein H T，Palmer S J P，et al.Quasistatic studies of the deformation and failure of β-HMX based polymer bonded explosives［J］.Proc R Soc Lond A，2002，458:743-762.

［9］Skidmore C B，Philips D S，Son S F，et al.Characterization of HMX particles in PBX9501［C］. The 10th American Physical Society topical comference on Shock Compression of Condensed Matter，1998，429:579-582.

［10］陈鹏万，黄风雷.用巴西实验评价炸药的力学性能［J］.兵工学报，2001，22(4):533-537.

［11］Rae P J，Goldrein H T，Palmer S J P，et al.Quasi-static studies of the deformation and failure of PBX 9501［J］. Proc R Soc Lond A，2002，458:2227-2242.

［12］Cheng Liu，Darla G Thompson，Manuel L Lovato，Racci Deluca.Macroscopic Crack Formation and Extension in Pristine and Artificially Aged PBX 9501［C］.In:14th International Detonation Symposium，2010.

［13］罗景润.PBX 的损伤、断裂及本构关系研究［D］.绵阳:中国工程物理研究院，2001.

［14］Skidmore C B，Phillips D S，et al.Microscopical Examination of Plastic-Bonded Explosives［J］. Microscope 1997，45(4):127-136.

［15］Chen Pengwan，Huang Fenglei，Dai Kaida，et al. Detection and characterization of long-pulse low-velocity impact damage in plastic bonded explosives［J］. International Journal of Impact Engineering，2005，31(5):497-508.

［16］H Trumel，P Lambert，R Belmas.Mesoscopic Investigations of the Deformation and Initiation Mechanisms of a HMX-based Pressed Composition［C］.In:14th International Detonation Symposium，2010.

［17］梁增友.炸药冲击损伤与起爆特性［M］.北京:电子工业出版社，2009.

［18］高登攀，田勇.高聚物粘结炸药热冲击过程中的声发射现象研究［J］.无损检测，2006，28(4).

［19］蓝林钢，温茂萍.JOB-9003 炸药疲劳过程声发射研究［C］.2005年火炸药学术研讨会论文集:102-108.

［20］周风华，王礼立，胡时胜.有机玻璃在高应变率下的损伤型非线性粘弹性本构关系及破坏准则［J］.爆炸与冲击，1992，

12(4):333-342.

［21］李英雷，李大红，胡时胜，等.TATB 钝感炸药本构关系的实验研究［J］.爆炸与冲击，1999，19(4):353-359.

［22］罗景润，李大红.简单拉伸下高聚物粘结炸药的损伤测量及损伤演化研究［J］.高压物理学报，2000，14(3).

［23］Dienes J K.Foundations of statistical crack mechanics［C］.International Symposium on Intense Dynamic Loading and Its Effects.1986:602-607.

［24］Dienes J K. A Statistical Theory of Fragmentation Processes［J］.Mechanics of Materials，1985，4(3-4):323-335.

［25］Dienes J K.Statistical Crack Mechanics［J］.Proceedings of the Shock Mechanics and Thermal Initiation Workshop held at LANL on November 16-18，1993.

［26］Bennett J G，Haberman K S，Johnson J N etc. A constitutive model for the non-shock ignition and mechanical response of high explosives［J］. Journal of the Mechanics and Physics of Solids 46，1998(12):2303-2322.

［27］Robert M. Hackett and Joel G. Bennett. An implicit finite element material model for energetic particulate composite materials［J］.International Journal for Numerical Methods in Reengineering，2000，49(9):1191-1209.

［28］Addessio F L，Johnson J N.A constitutive model for the dynamic response of brittle materials［J］.Journal of Applied Physics 67(7):3275-3286，1990.

［29］Dienes J K，Middleditch J，et al. Progress in Statistical Crack Mechanics:an Approach to Initiation［C］. In:12th International Detonation Symposium，2002.

［30］Dienes J K.Multiple-Shock Initiation via Statistical Crack Mechanics ［C ］. In: 11th International Detonation Symposium，1998.

［31］Dienes J K，Zuo Q H，Kershner J D.Impact initiation of explosives and propellants via statistical crack mechanics［J］.Journal of the Mechanics and Physics of Solids，2006，54:1237-1275.

［32］Williamson D M，Siviour C R，Proud W G，et al.Temperaturetime response of a polymer bonded explosive in compression(EDC37)［J］.Journal of Physics D:Applied Physics，2008，volume 41.

［33］李敬明，温茂萍，黄毅民.热循环对TATB 基高聚物粘结炸药性能的影响研究［J］.含能材料，2005，13(4):208-210.

［34］Trevor M. Willey，Lisa Lauderbach，Franco Gagliardi，et al.Comprehensive Characterization of Voids and Microstructure in TATB-based Explosives from 10 nm to 1 cm:Effect of Temperature Cycling and Compressive Creep［C］.In:14th International Detonation Symposium，2010.

［35］田勇，罗顺火.JOB-9003 炸药“激热”冲击损伤破坏及超声特征［J］.火炸药学报，2002(3):19-21.

［36］田勇，张伟斌.炸药热冲击损伤破坏及超声波特性参量检测［J］.火炸药学报，2000(4):13-15.

［37］田勇，张伟斌.JOB-9003 高聚物粘结炸药热冲击损伤破坏相关性研究［J］.含能材料，2004，12(3):174-177.