夹心式低频超声换能器设计

曾一平，李 剑，刘 瑜，彭 炯

(第二炮兵工程大学，西安 710025)

对于纯粹的压电陶瓷元件来说，要得到共振频率在50 kHz 以下的振子，沿其极化方向的厚度应为4 cm 以上。这样厚的振子，内部阻抗太高，而且烧成和极化工艺都较困难。为了克服这一困难，常采用一种在压电陶瓷圆片的两端面夹以金属块而组成的夹心式压电陶瓷换能器［1］，图1 所示该换能器主要由中央压电陶瓷片、前后金属盖板、预应力螺栓、金属电极片以及预应力螺栓绝缘套管等组成。

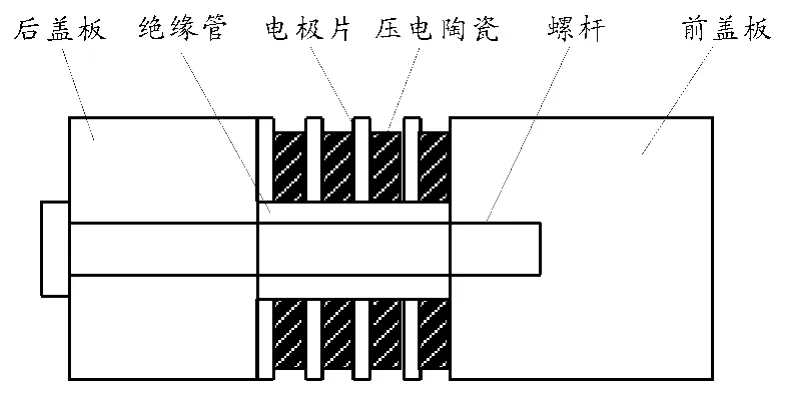
图1 夹心式换能器结构示意图

这种换能器应用非常广泛，文献［2］中利用该换能器的结构设计制作了非金属检测探头，并对混凝土进行了检测;文献［3］中在该型换能器前端安装一个变幅杆应用于超声加工领域。在夹心式换能器中，通过改变压电陶瓷材料的厚度和形状以及前后金属盖板的几何尺寸和形状，可以对换能器进行优化设计，来获得不同的工作频率和其他一些性能参数，以适应不同的工作环境和应用场合。在一般情况下，利用换能器的频率方程设计换能器的方式有2 种:一种是给定换能器的频率，利用频率方程设计换能器的形状和尺寸;另一种是给定换能器的材料和几何尺寸，由频率方程计算其共振频率。本文对换能器的几种设计方法进行了论述和推导，分析了它们各自的特点，提出简化设计的方法，并找出了影响设计精度的原因，对工程上换能器的设计有一定指导作用。

1 解析法

依据一维细棒振动原理，列出每个振动元件的波动方程，写出通解，利用边界条件确定出方程中的待定系数，再利用连续性条件解方程组可导出换能器的频率方程等各性能参量的解析表达式。

在图2 所示换能器的简化模型中，1，2，3 分别表示换能器的后盖板、压电陶瓷晶片、前盖板，质点位移为ξ(x)，F 为应力，V 为振速，c 为声速，k 为波数，当换能器的横向尺寸小于时，由一维细棒的振动原理，得到各元件波动方程简谐解［4-5］

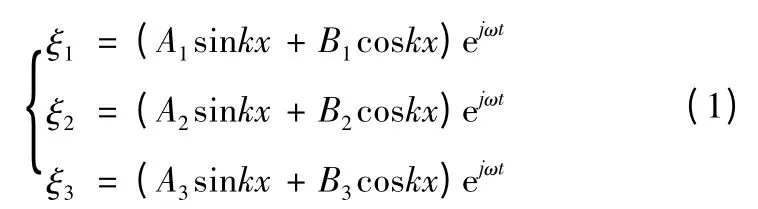
图2 换能器简化模型

由换能器端面的边界条件和交界面处力与速度的连续条件。可得到下列方程组

由式(1)和(2)联立，即可得到换能器的频率方程及其他所需的设计参量。

该方法是最基础的设计方法，由振动理论、波动方程、压电方程，结合边界条件和连续性条件推导出来的，其他的方法都是在它的基础上优化变换得到的。需要指出的是，前后盖板的形状在很多情况是变截面，有圆柱形、圆锥形、指数形、悬链线等复杂形状，可根据不同需要进行选择，当选择较为复杂的截面形状时，用该方法计算比较复杂;为简化设计，往往假设负载为零即F3(L3)=0，但很多情况下要考虑负载，因为负载对设计有一定影响，但当F3(L3)≠0 时，用该方法计算较为复杂［6］。

2 等效电路法

将作用在换能器每个元件两端的力、振速、力阻抗分别类比于电压、电流、电阻抗，则换能器和电路之间就有等效关系，这就是力电类比方法［7］。如图2 所示的换能器的三大部分，每个元件用力电类比的方法，可得到等效的机械四端网络［8］如图3、4、5 所示，网络中各等效电阻Z 都可由力电类比求得。由于边界振速连续，可将各元件的等效T 型网络连接起来，得到整个换能器的等效电路如图6，图6 中Zbl、Zfl为分别是换能器前后辐射面的负载阻抗，一般情况下，Zbl=0，由于换能器的前表面与负载相连，因此对应不同的负载，Zfl有不同的值。令电路阻抗部分为零，就可得到该换能器的频率方程，也可对换能器的尺寸进行设计。

该方法利用等效电路图显示比较直观，物理意义清楚，可以利用电路的原理进行分析计算。然而，从具体的推导过程中可以发现，利用这一方法得出的换能器的频率方程是一个非常复杂的超越方程，其求解非常困难。此时利用换能器的节面可以简化设计。对于半波振子，在振动时，换能器的两端振动位移最大，而在换能器的内部某个位置，存在一个振动位移为零的截面，称为节面。因此，在设计压电换能器时，假如我们将此位移节面作为一个分界面，把整个换能器看成是由2 个四分之一波长的振子组成，就可以利用这2 个四分之一波长振子的等效电路求出其频率方程，从而就可以得出换能器的整个频率方程［9］。如图2 所示，AB 表示换能器的位移节面，它将换能器分为2 个四分之一波长的振子，每个四分之一波长的振子都是由压电陶瓷晶片和金属盖板组成的，金属盖板可以看成是压电陶瓷的负载。图7 表示一个位于位移节面右边的四分之一波长振子的机电等效电路图。由于位移节面处的位移振速等于零，因此四分之一波长振子等效电路的左边可以看成是开路的，其频率方程可由回路中总电抗为零的条件来得出，由此可以得出换能器位移节面右边四分之一波长振子的频率方程，同理对于换能器位移节面左面四分之一波长振子的频率方程，这样就可以对换能器的形状、尺寸及共振频率进行设计。

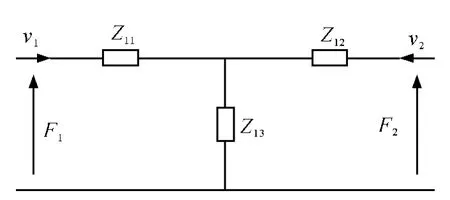
图3 元件1 的等效T 型网络

图4 元件2 的等效T 型网络

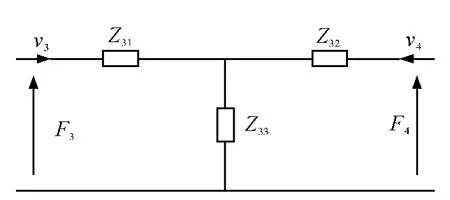
图5 元件3 的等效T 型网络

图6 换能器的等效电路

图7 节面右边四分之一波长振子的等效电路

3 传输矩阵法

根据一维振动原理，换能器的每个振动元件都有其等效的四端网络，由波动方程的通解，求出四端网络两端速度与力的关系，并将这一关系用矩阵表示。矩阵中的各个元素由元件的材料及形状决定，由振动理论可求得。把3 个元件的四端网络按组合顺序串联起来，将各网络矩阵相乘，可简化为一个换能器总体四端网络［10-12］。利用换能器两端自由的条件得到系统的谐振频率。

将换能器各元件看作是一维纵振动，其四端网络如图8所示，写成表达式为

由细棒纵振动的波动方程，可得

图8 四端网络

如图2 所示换能器由3 个元件组成，各元件分别按顺序标以1，2，3。F1，V1，F2，V2，F3，V3，F4，V4分别表示各个元件两端的力与振速，根据前面的讨论有第i 个元件的等效四端网络为

由连续性条件，将3 个元件的四端网络联立得换能器的四端网络，如图9 所示。

图9 换能器的等效四端网络

将该式(6)进行简化，则

由换能器两端自由，得边界条件，F1=F4=0，则得

这种方法很简单方便，利用计算机辅助设计能较好运用在工程设计上，特别针对不同形状的前后盖板，利用传输矩阵编成子程序，设计时按需要进行调用，不仅方便设计，在理论上也接近实际。需要注意的是，传输矩阵法只适应于单纯振动的换能器，如果存在复合振动，如纵弯、纵扭等，这种方法将不再适用。

4 有限元法

常用的有限元设计换能器的软件是ANSYS。其设计的一般步骤有:预处理、前处理、求解、后处理［13］。如图10 所示。有限元方法对换能器建模时，一旦完成对换能器的建模，其计算过程就比较简单，而且计算结果是以数值解给出的，通过可视化编程，后处理模块可将这些数值解以图形的方式显示出来，由此观察到换能器的各个振动模态、位移分布以及应力分布。有限元方法特别应用于不规则的、无法得到解析解的换能器的设计上。

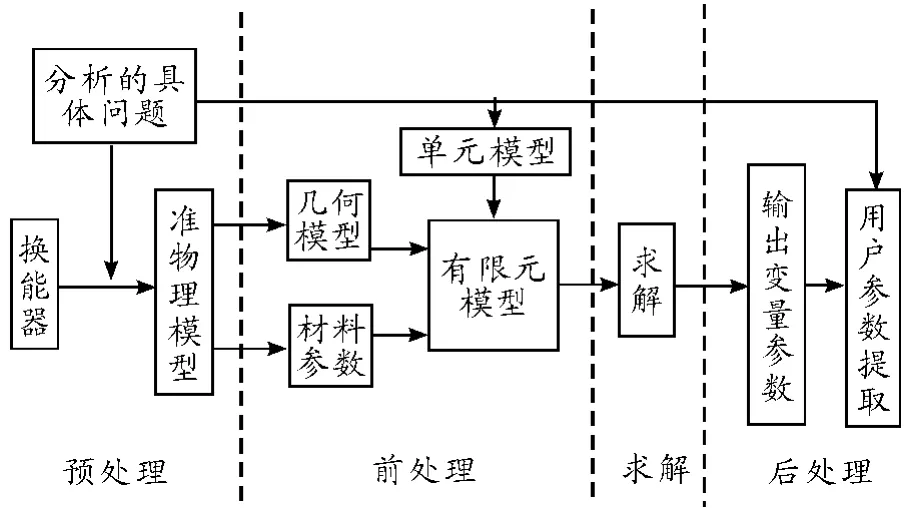
图10 ANSYS 设计换能器的一般步骤示意图

5 结束语

传统的解析法和等效电路法设计分析换能器时，会有较大的局限性:它们都要对被分析对象建立简化的数学模型，如等效电路法处理的对象是集中参数系统，因而它只能得出换能器处于谐振状态时(这时可简化为集中的参数系统)的一些参数;又因为得出的性能参数都是以解析式的形式表达出来，所以要确切地知道换能器系统内部的如位移分布、应力分布等量，都要经过很繁琐的运算才能得到。传输矩阵法有效地避免了这一问题，特别是针对复杂形状函数换能器性能表达式复杂、计算工作量大的难点，通过计算机编程，能方便地对换能器进行设计。而有限元法通过可视化的特点，不仅能对换能器性能参数进行设计，还可以显示换能器内部位移分布和应力分布情况，适合对换能器进行分析验证。

在实际的设计中我们可以根据需要选择不同设计方法。针对不同的研究对象，有时候可将几种方法结合起来使用，以简化设计，另外使用不同方法也可以相互验证。比如，对一端带有圆锥杆的换能器，就可以用传输矩阵法进行设计，用有限元方法进行验证。对于工程应用，换能器的设计应该系列化，假定有一“最佳”设计的参考换能器，谐振频率为ω0，根据需要新设计的频率ωs，确定频率比例因子s=ωs/ω0，按比例改变参考换能器的尺寸，得到的新换能器除少数性能参数有规律地变化外，其他性能参数不变，可以极大地简化设计。同时如果能用设计方法本身统一换能器各元件性能参数的表达式，就可以方便地设计，而且用统一的表达式，也能更方便更深入地研究换能器的声学性质。

然而，在利用以上方法能对换能器进行设计时，由于建模过程中进行了简化，实验值与理论值存在一定的误差，通过分析，得到影响设计精度的原因有:

1)探头中预应力螺栓对换能器性能参数的影响。文献［14］中的研究结果表明，当螺栓的长度、直径和位置变化时，换能器的共振频率变化可达1.3kHz，而有效机电耦合系数的相对变化可达25.5%。设计螺栓时，适当设计螺栓的长度和减小螺栓的直径，可提高换能器的机电耦合系数。

2)节面选择对换能器性能参数的影响。文献［15］中分别对3 种节面位置进行了分析，得出其在换能器尺寸、前后振速比和有效机电耦合系数方面3 种特殊位置公式，并进行对比分析，不同位置这3 个设计参数有较大差距。可根据不同的设计需要，选择不同的节面位置。

3)负载对换能器性能参数的影响。设计时为简化，忽略了负载的影响，然而在实际工作过程中，换能器都是有负载的，而且对换能器的频率影响也比较大。在换能器的材料、形状和几何尺寸给定后，其共振频率仅由换能器的负载确定。

4)横向耦合效应对换能器性能参数的影响。为简化设计，将换能器各元件都看作纯纵向振动，然而实际上过程中存在横向耦合振动，引起固有频率下降。纵振动固有频率的下降与换能器径长比有关，径长比越大，固有频率下降程度就越严重。

在实际设计过程中，要综合考虑以上因素，才能进一步提高设计的精度。

［1］林书玉.超声换能器的原理及设计［M］.北京:科学出版社，2004:91-111.

［2］周光平，龙飞，邱志宇.低频超声检测探头的研制［J］.南昌航空工业学院学报，1994(2):78-82.

［3］李贵花，张向慧.带有1/4 波长指数形复合变幅杆的超声换能器设计［J］.机械设计与制造，2009(5):1-3.

［4］Mason W P. Physical Acoustics Principles and Methods［M］.London:Aeademic Press Inc，1964.

［5］Mason W P.Elcetromechanical Transducers and Wave Filters［M］. Second Edition. D. Van Nostrand Company Inc，1948.

［6］林仲茂.有力、电负载和损耗时夹心式压电换能器的共振频率及效率［J］.应用声学，1983，2(1):22-27.

［7］左鹤声.机械阻抗方法与应用［M］.北京:机械工业出版社，1987:74-80.

［8］黄德中.超声波振动器四端网络设计［J］.振动与冲击，2005，24(5):107-108.

［9］王建平.大振幅夹心式复合换能器的研制和动态特性研究［D］.焦作:河南理工大学，2005.

［10］凌鸿烈.半波长夹心式换能器的理论分析和计算［J］.声学技术，1992，11(4):35-38.

［11］黄振伟，傅波，穆飞.夹心式压电换能器串并联传输矩阵设计法［J］.应用声学，2008，27(5):395-400.

［12］俞宏沛.超声换能器、变幅杆及其组合的一种计算方法［J］.应用声学，1988，7(4):30-36.

［13］原林.夹心式纵弯振动换能器特性研究及有限元仿真［D］.西安:陕西师范大学，2007.

［14］李军，贺西平，丁少虎.预应力螺栓对压电换能器性能参数的影响［J］.压电与声光，2010，32(6):985-990.

［15］霍树青，高长水.夹心式换能器设计中节面位置的选择与分析［J］.电加工与模具，2009(2):47-49.