基于BP 神经网络的数控机床主轴性能评估模型

胡跃强，李 苓，高宏力，章 健，李文涛，钱士才

(西南交通大学 机械工程学院，成都 611756)

数控机床及由数控机床组成的制造系统是改造传统产业、构建数字化企业的重要基础装备，其发展一直备受人们关注。数控机床是现代机械制造业的主流装备。用数控机床提升传统制造业装备水平的重大意义，已经成为有关各界人士的共识。现在数控机床正朝着高效高速化、高精度、可重构方向发展，并已成为当前数控机床发展的基本趋势。

在生产过程中，随着数控机床各个部件性能的不断退化，数控机床故障发生频繁，不仅增加企业的维护成本，而且影响企业的生产效率、造成经济损失。主轴作为数控机床的关键部件，其在加工过程中的精度及加工性能的变化将严重影响产品的加工精度。目前，国内外研究人员针对主轴系统的振动测试、建模分析和性能预估做了大量的研究，提出了多种主轴系统动力学特性分析方法。但是，针对实现加工过程中的动态性能评估还缺乏系统性研究，其中对一些影响主轴动力学分析精度的关键问题，还处于空白研究领域。本文通过对主轴部件动态特性进行分析研究，采用人工智能技术建立传感器信号与加工性能之间的非线性映射关系，可丰富动态特性评估的理论知识，实现性能的在线评估。这对于解决机床主轴的主动维护具有重要的经济及战略意义。

1 BP 神经网络介绍

神经网络(neural netwoks，NN)是由大量的、简单的处理单元(简称神经元)广泛互相连接而形成的复杂网络系统，他反映了人脑功能的许多基本特征，是一个高度复杂的非线性动力学系统。神经网络具有大规模并行，分布式存储和处理，自组织、自适应和自学习能力，特别适合处理需要同时考虑许多因素和条件的、不精确和模糊的信息处理问题。神经网络的发展与神经科学、树立科学、认知科学、计算机科学、人工智能、信息科学、控制论、机器人学、微电子学、心理学、光计算、分子生物学等有关，是一门新兴的边缘交叉学科。

1.1 BP 神经网络简介

BP(back propagation)网络是一种按照误差反向传播算法训练的多层前馈神经网络。基于BP 算法的二层网络结构如图1 所示，包括输入层、一个隐层和输出层，三者都是由神经元组成的，输入层各神经元负责接收并传递外部信息，中间层负责信息处理和变换，输出层向外界输出信息处理结果。神经网络工作时，信息从输入层经隐层流向输出层，信息正向传播，若现行输出与期望相同，则训练结束，否则，误差反向进入网络，误差反向传播，将输出与期望的误差信号按照原连接通路反向计算，修改各层权值和阈值，逐次向输入层传播。信息正向传播与误差反向传播反复交替，网络得到了记忆训练，当网络的全局误差小于给定的误差值后学习终止，即可得到收敛的网络和相应稳定的权值。网络学习过程实际就是建立输入模式到输出模式的一个映射，也就是建立一个输入与输出关系的数学模型。

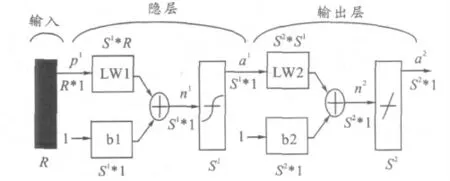
图1 基于BP 算法的二层网络结构

1.2 BP 神经网络的建立

BP 神经网络的学习步骤可以简单描述如下。

1)将样本输入、输出参数归一化为［0，1］区间。

2)赋(-1，1)之间的随机参数作为权值初值。

3)将样本的数据赋给输入层相应的节点，依照权值和激励函数的作用，在输出节点算出网络输出值。

4)计算网络输出与样本点真实输出之间的相对误差。

5)如果相对误差大于给定误差，则按学习方法修正权值，转到步骤3)重新计算;如果相对误差小于或等于给定误差，则BP 神经网络学习完毕。

2 主轴振动试验介绍

本试验是对长征718 机床进行的主轴箱振动试验，主轴转速为2 000转，采样频率分别是16 kHz，分别对正常机床和故障机床进行数据采集，试验中机床故障原因为主轴轴承组出现故障。图2 为数据采集原理图。本试验在主轴箱多个位置安装了振动加速度传感器，主轴转动后，进行数据采集，传感器采集信号后，经信号调理器和A/D 转换后输入到计算机，存档，方便后续分析使用。试验中每个位置不同时间分别测了5 组数据。

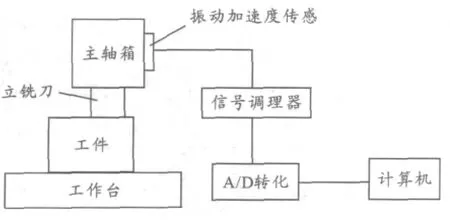
图2 数据采集原理

3 特征提取

3.1 数据预处理

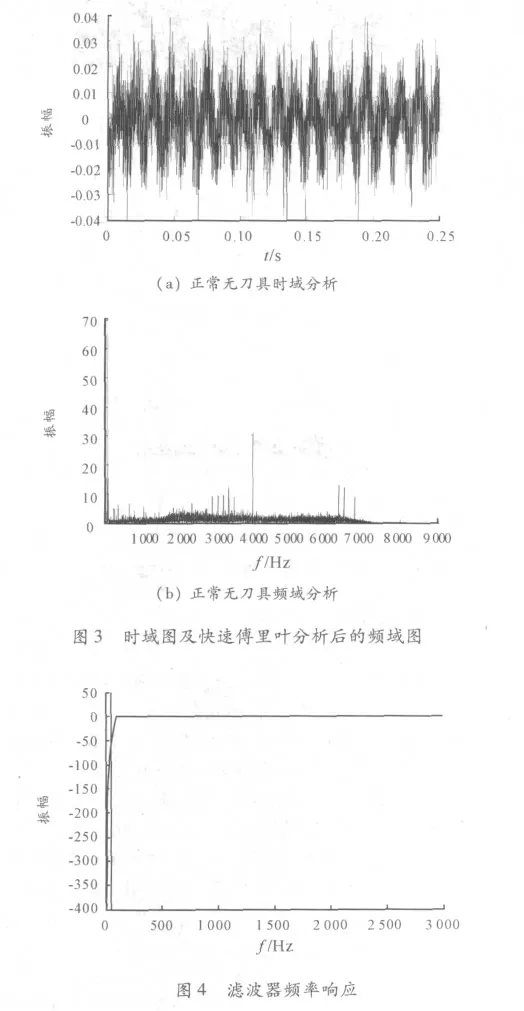
由于机床实际工作环境中，有很多振动等干扰，所以在得到上述实验数据后，需进行预处理，即将其干扰的频率成分滤去，得到真实机床工作的时域和频域图。图3 为长征718 机床在正常无刀具空转时的1 组实验数据的时域图以及快速傅里叶分析后的频域图。

由图3 可看出，在低频区有一频率干扰很大，计算得此频率点在50Hz 左右，所以需要进行滤波处理。

3.2 Butterworth 滤波技术

Butterworth 低通滤波器是一种全极点配置的滤波器，具有本质的稳定性。Butterworth 低通滤波器具有最大平坦幅频响应的特性，且具有良好的线性相位特性等优点，故目前广泛采用。低阶Butterworth 低通滤波器响应速度快，超调量小，稳定性好，但是检测精度差;高阶Butterworth 低通滤波器检测精度好，但是响应速度慢，超调量大，稳定性差。

在matlab 中，可利用buttord 函数求得butterworth 滤波器需要的最小阶数和截止频率，再利用butter 函数快速生成所需要的滤波器。图4 为滤波器的频率响应图。

对实验数据进行butterworth 滤波后，滤去低频干扰，得到滤波后的数据时域分析图和频域分析图，如图5 所示。

由图5 可看出，butterworth 滤波效果良好，低频信号干扰成功滤去，以便下文特征值提取。

3.3 特征选择

特征选择的好坏严重影响识别模块的性能，作为模式识别中的一个重要问题，特征选择受到研究人员的高度重视。在许多实际问题中，常常不容易找到那些重要的特征，这使得特征提取成为构造模式识别系统最困难的任务之一。

一般地，有效特征值选择原则有以下2 点:①同状态信号重复性好;②不同状态信号差异性好。

图5 滤波后数据时域分析图和频域分析图

3.3.1 时域特征提取

对于振动信号，常选用时域波形的峰值Peak、有效值RMS、均方值DAL 等有量纲参数来衡量设备故障有无及其发展趋势。但这些参数依赖历史数据并且对载荷和转速等的变化比较敏感。用无量纲参数指标判断滚动轴承故障基本上不受轴承型号、转速和载荷等因素的影响，无需考虑相对标准值或与以前的数据进行比较;所有测点即使同以往的地方略有变动，也不致对诊断结果产生太大的影响。经常用到的无量纲特征参数有峰值因子(C)、峭度因子(K)、裕度系数(L)、脉冲因子(I)、波形因子(S)等。

1)峰值因子(C)

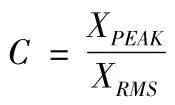
式中:XPEAK为信号的峰值。利用峰值计数法从{xi}的N 个值中找出n 个峰值{xpi}(j =1 ～n)，则{xi}的峰值指标为:

2)峭度因子(K)

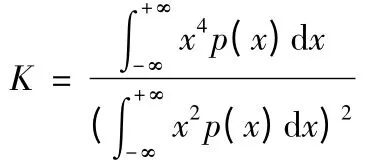
3)裕度系数(L)

4)脉冲因子(I)

5)波形因子(S)

在Matlab 中对实验数据进行时域特征提取，并作归一化处理，可得表1。

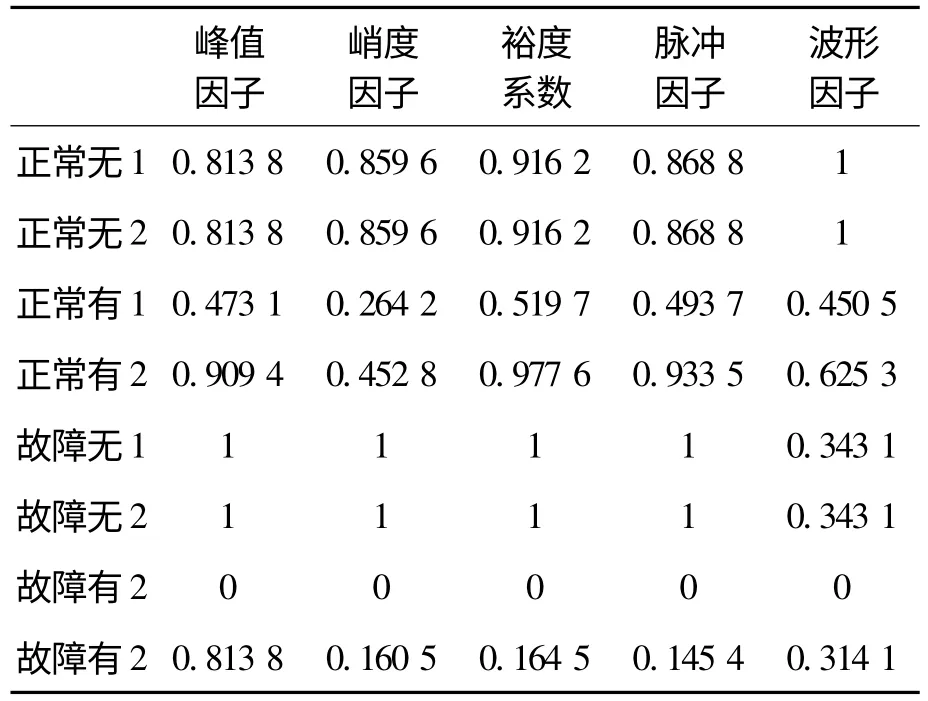
表1 时域特征提取值(归一化)

3.3.2 频域特征提取

在滚动轴承振动信号分析中，常用到的频域参数有重心频率FC、均方频率MSF、均方根频率RMSF、频率方差VF、频率标准差RVF 等。对于滚动轴承，其特征频率峰值也可以作为特征参数诊断故障。虽然滚动轴承故障特征频率用来确定故障类型或位置，但是在频谱图上这些频率成分的幅值不一定很突出。这是由于故障可能激起系统的高频振动，使得特征频率点幅值相对于共振峰值较低，甚至被抑制。所以在此使用下述的频率特征参数:

1)重心频率FC

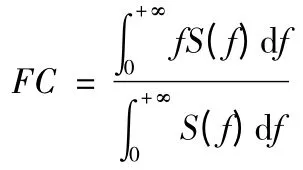
2)均方频率MSF

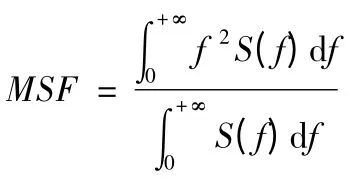
3)均方根频率RMSF

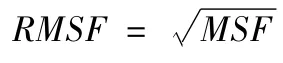
4)频率方差VF

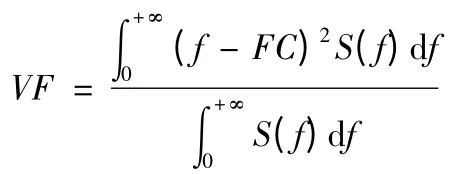
5)频率标准差RVF

上式中的S 均为信号功率谱。其中，重心频率FC、均方频率MSF 和均方根频率RMSF 都是描述功率谱主频带位置变化的;而频率方差VF 和标准差RVF 描述能量的分散程度。由于计算机在计算时，频谱要离散化，分析频率受采样频率fs 的限制。为了能实现对滚动轴承工况的在线监测与诊断，希望能快速算出以上的参数，利用傅里叶变换性质，可得出上述3 个参数的时域快速算式如下:

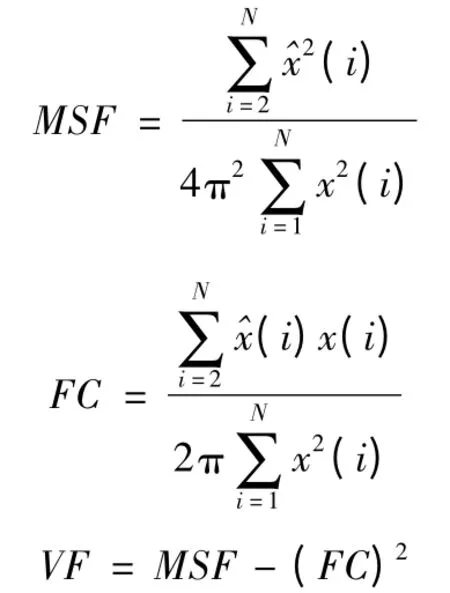
在Matlab 中，编程计算各特征值，列于下表2。

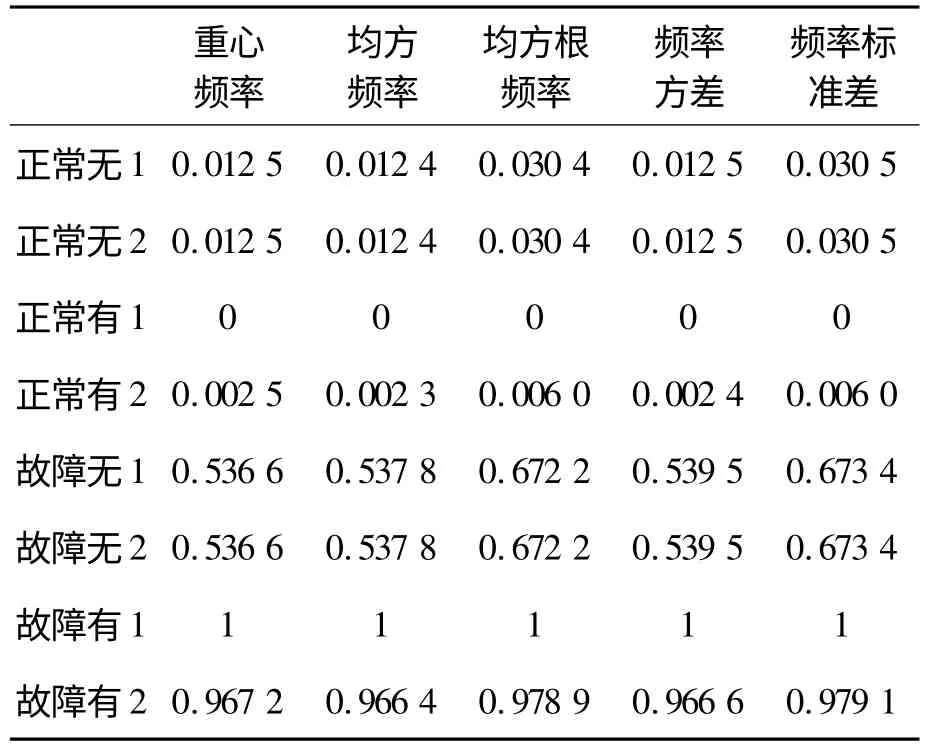
表2 频域特征提取值

4 BP 神经网络的建立

4.1 建立网络

3)选择学习率η，动量因子α，精度ε，最大训练次数tmax。

4)k=1，t=0，迭代开始。

5)计算网络阴层单元和输出层单元的实际输出

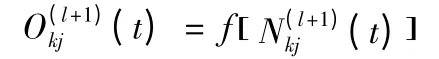
6)计算训练误差。

输出层:

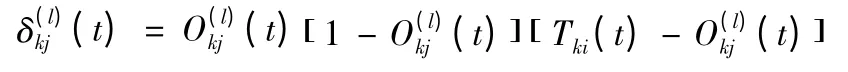
隐含层:

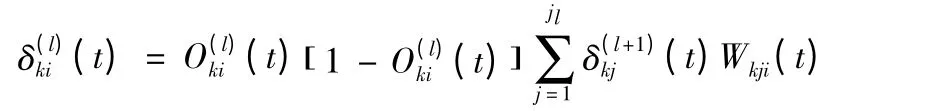
7)修正权重和误差阈值。

权重:

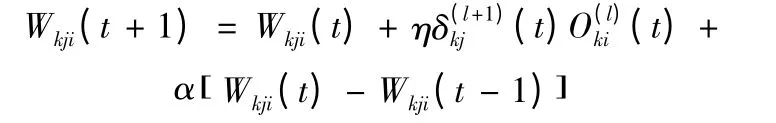
阈值:

8)k=k+1，重复步骤5)～6)，直至k=P。

9)计算输出层均方误差

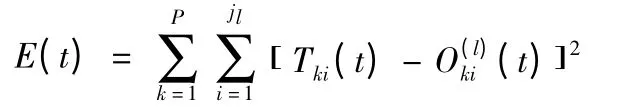
10)若E(t)＞ε，t = t + 1，重复步骤5)～8)，直至E(t)≤ε或t ＞tmax，训练结束。

在Matlab 中，利用newff 函数生成BP 网络，隐层神经元传递函数tansig ()，输出层神经元传递函数purelin ()，训练函数trainlm。

参数选择如下。

隐含层数:理论分析，具有单隐层的BP 网络可以映射所有的连续函数，因此选取单隐层的BP 网络。

节点数:由于输入特征值有10 个，所以节点数为10;输出为工作状态，正常或故障，所以1 代表正常，0 代表故障，节点数为1。

隐层节点数由经验公式有

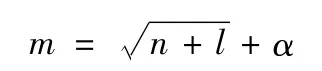
式中:m 为隐层节点数;n 为输入节点数;l 为输出节点数;α为1 ～10 的常数。本文取隐层节点数为8。

4.2 训练网络

上述特征值每种工况有2 组数据，取每种工况的其中1组作为训练网络的输入，期望输出为［1 1 0 0］，1 代表机床正常，0 代表机床故障。在Matlab 里利用train 函数进行网络训练，训练过程如图6 所示。

4.3 测试网络

再将4 种工况的另1 组数据作为网络输入，输入已训练好的网络，进行网络测试。在matlab 中利用sim 函数进行仿真。得网络输出为［1.000 0 1.086 3 0.000 0 -0.195 4］，最后得正确率达92.95%。

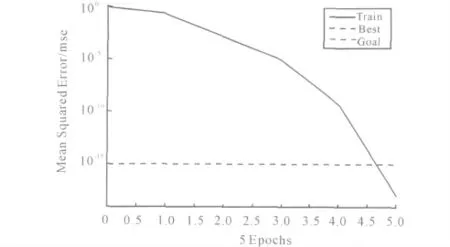
图6 train 函数网络训练过程

5 结束语

本文介绍的方法是一种人工智能的新型研究方法，能够对机床进行仿真模拟，并实现数字化。对机床主轴的各项性能能够进行数据采集，智能化了解主轴的工作状况。利用软件分析主轴工作状态的运动指标，充分实现人工智能化。

对于主轴的动态性能研究，从时间与过程的角度，旨在为提高主轴运作的高效性与准确性提供依据，如此可以提高加工精度。动态性能包括力学性能，振动频率等各种性能。对机床主轴工作状态下的动态性能的评估，能更好地把握机床的工作性能与机床的发展。

［1］李冬梅.基于时延相关解调与B 样条模糊神经网络的轴承故障诊断［D］.成都:西南交通大学，2008.

［2］王长青，李爱军，王伟.Butterworth 滤波器在飞行控制系统设计中的应用［J］.飞行力学，2009，27(1):74-76.

［3］安妮、徐建民.齿轮箱振动的故障诊断与分析［J］.武汉工程大学学报，2011，33(12):70-72.

［4］杜娟，阎献国，韩建华，兰国生.基于混合神经网络的数控机床故障诊断技术研究［J］.组合机床与自动化加工技术，2011(12):32-34.

［5］唐贵基，杨玉婧，宋彩萌.基于神经网络的旋转机械振动故障诊断［J］.机械工程师，2012(1):47-49.