于成拱桥吊杆施工索力优化

莫晓华，陈文杰

中、下承式拱桥受力良好，在一些地势较为平坦的地区较为常见。吊杆是中、下承式拱桥的关键构件，若因施工不当、养护不到位等原因，则可能导致较为严重的破坏［1］。施工过程的吊杆索力则直接决定着结构的受力状况和吊杆的成桥索力，也影响着后期运营过程的可靠性。本文以一座下承式拱桥为例，基于实际施工过程和吊杆索力的实测数据，利用有限元方法对其受力状况进行了分析，并采用影响矩阵法［2］，对吊杆索力进行调整优化以改善桥梁受力。结果表明:通过调整索力结构受力得到较为明显改善，且成桥后吊杆索力和主拱圈等受力均较为对称均匀。

1 工程概况

于成桥为计算跨径90 m的钢管混凝土拱桥，拱轴线为二次抛物线，矢跨比为1/5，拱肋断面形式为长方形，横向设置三片拱肋，一片中拱肋和两片边拱肋。中拱肋高 1.4 m，宽 1.6 m，边拱肋高 1.4 m，宽0.85 m，三片拱肋均由2 cm钢板组成，拱肋间设置5道“一”字型风撑。纵梁为预应力混凝土结构，中纵梁截面尺寸高2.2 m，宽1.4 m。边纵梁截面尺寸为高 2.2 m，宽 1 m。预应力钢束采用标准为1 860 MPa标准强度的高强低松弛钢绞线。

全桥共设18道横梁，其中2道为预应力混凝土端横梁，16道为中横梁，中横梁采用“T”字型截面，端横梁采用单箱双室截面。

吊杆采用可换式吊杆纵向间距为5 m，横桥向中心距为18 m。吊杆为工厂生产，现场安装，中拱肋吊杆采用PESM7－127，边拱肋采用PESM7－73。

2 调整前受力状况

由于通航影响和支架搭设时考虑不周等原因，施工步骤被迫临时改变，出现了不对称的施工过程，导致在浇筑完主梁后，于成桥受力状况较为不合理，以下列出吊杆索力和主拱圈的数据。

2.1 吊杆索力

利用频率法，对于成桥索力进行了现场检测，实测索力见表1和图1，可知:调整前的索力不均匀，不对称，东西侧索力偏差较大。

2.2 主拱圈应力

利用有限元分析软件，建立于成桥模型，并按照实际施工步骤模拟施工过程，结合表1索力，计算得到索力调整前于成桥主拱圈应力(由于数据过多仅列出主拱圈数据)见表2。可知:管内混凝土最大组合压应力10.7 MPa，主拱钢管最大组合压应力107 MPa;钢管和管内混凝土应力在纵向和横向均存在一定程度的不对称，其中15 m截面位置处西侧钢管组合压应力比东侧大31.7%，西侧管内混凝土组合压应力比东侧大45%。

表1 调整前实测索力

续表1 调整前实测索力

图1 调整前实测索力

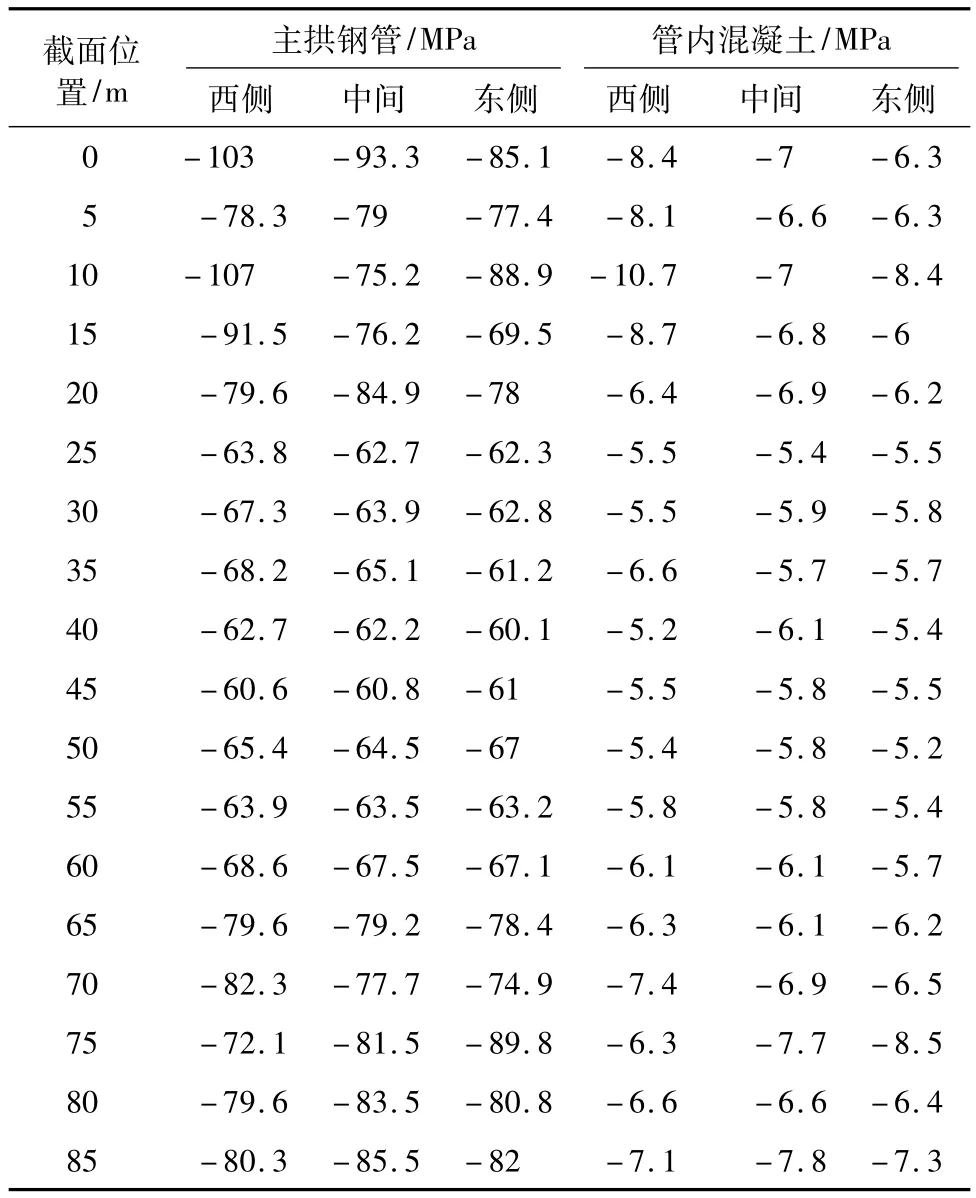
表2 现阶段主拱圈应力

3 索力调整

3.1 索力调整原理

本次索力优化以位移控制为主，保证成桥线形满足目标值，设关心截面的位移向量为{x0}，索力对位移的影响矩阵为［C］，则当索力调整向量为{T}时，位移变为:

取目标函数为:

则可得到索力优化方程:

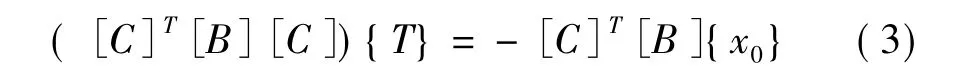
其中:［B］为权矩阵，实际计算时取为单位矩阵。

3.2 索力调整目的和流程

从索力实测数据可知，于成桥索力分布不对称，不均匀。因此，本次索力调整主要目的为:

1)使吊杆索力在纵向、横向均对称;

2)使同一索面吊杆索力分布均匀;

3)使主拱圈、主梁和横向联系受力对称。

索力调整时按照先依次调整 1#、3#、5#、7#吊杆，再依次调整 2#、4#、6#、8#吊杆的流程对称进行。

4 调整后受力状况

4.1 调整后吊杆索力

调整索力后全桥索力见表3。

表3 调整索力后的索力值

由图2及表3可知:调整后索力在纵向、横向均较为对称;同一索面的成桥索力较调整前均匀。

4.2 调整后应力

调整索力后全桥应力(由于数据过多仅列出主拱圈数据)见表4。与表2相比可知:管内混凝土最大组合压应力减小为8.0 MPa，主拱钢管最大组合压应力减小为94.0 MPa，且主拱圈受力较为对称均匀，应力最大偏差出现在25 m截面位置处，西侧钢管组合压应力比东侧小3.3%，西侧管内混凝土组合压应力比东侧小5.3%。

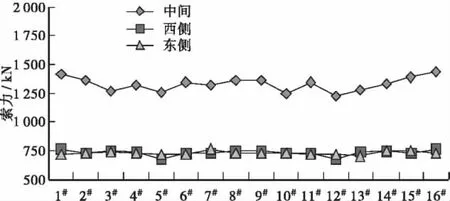
图2 调整后索力

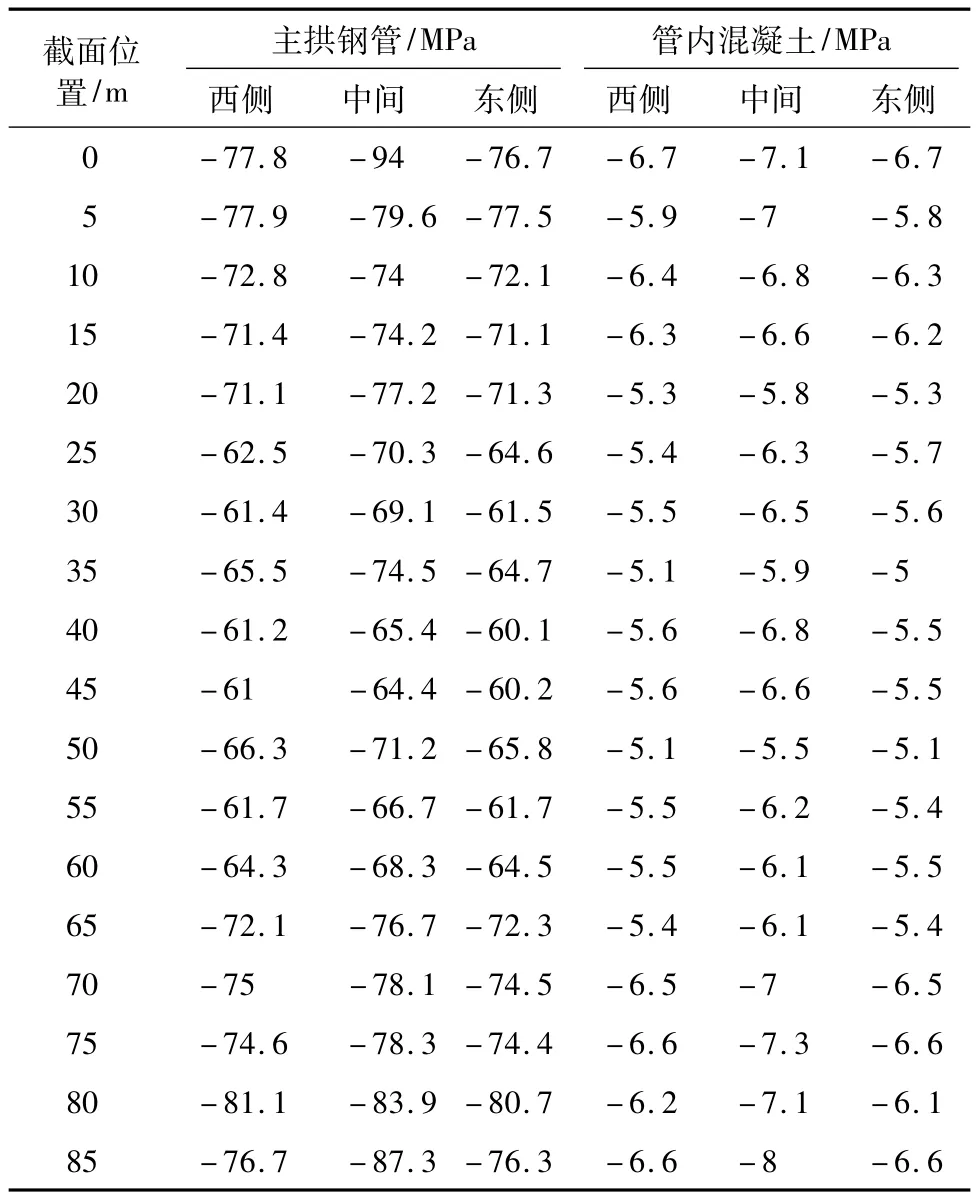
表4 成桥后主拱圈应力

5 成桥阶段受力状况

5.1 成桥阶段吊杆索力

按照以上调整，并完成后续施工，成桥阶段全桥索力见表5。

由图3及表5可知:成桥索力在纵向、横向均较为对称，最大偏差7.1%;同一索面的成桥索力较为均匀，达到了索力调整的目的。

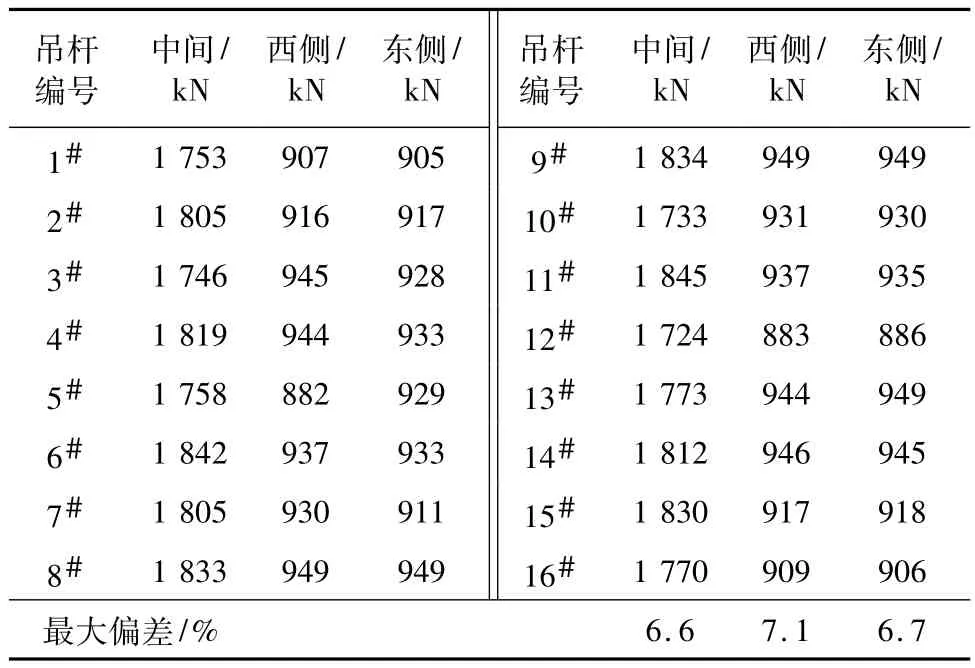
表5 成桥阶段索力值

图3 成桥阶段索力

5.2 成桥阶段应力

调整索力后成桥阶段全桥应力(由于数据过多仅列出主拱圈数据)见表6。可知:管内混凝土最大组合压应力9.7 MPa，主拱钢管最大组合压应力107.0 MPa，且主拱圈受力较为对称均匀，应力最大偏差出现在25 m截面位置处，西侧钢管组合压应力比东侧小2.9%，西侧管内混凝土组合压应力比东侧小4.2%。

表6 成桥后主拱圈应力

6 结语

1)索力调整后于成桥受力得到改善:管内混凝土最大组合压应力由10.7 MPa减小至8.0 MPa;主拱钢管最大组合压应力由107 MPa减小至94 MPa;

2)通过索力调整，于成桥成桥阶段索力和主拱圈受力较为对称、均匀，达到了索力调整的目的。

［1］陈 兵，朱正刚，罗特军.中、下承式拱桥吊杆体系研究［J］.四川建筑，2002，22(4):29 －31.

［2］肖汝诚，项海帆.斜拉桥索力优化的影响矩阵法［J］.同济大学学报，1998，26(3):235－240.