CCS-B船用钢的动态力学性能探究

诸葛骏，曹亚运，马 帅，沈超明，田阿利

(1.江苏科技大学能源与动力工程学院，江苏 镇江 212003;2.江苏科技大学船舶与海洋工程学院，江苏 镇江 212003)

0 引言

CCS-B船用钢属于低碳钢，在船舶行业中应用非常广泛。目前，我国在船舶的设计、强度验算等方面通常都基于材料的静态力学性能，而船舶，特别是军船，在实际服役期间遭受爆炸、高速碰撞等高强度瞬时冲击载荷而导致的损伤破坏却无法在静态力学范畴内分析解释，因而亟须对船用钢的瞬间动态力学性能进行深入研究。大量实验表明，多数材料在高应变率下表现出应变率相关性。因此，对船舶结构抗爆、强度计算等问题的理论分析和数值模拟分析，必须建立在已知材料的高应变率强度、断裂特性和应力—应变关系等本构关系的基础上。

目前，国内外许多学者对低碳钢材料的抗冲击性能已有一定的研究，曲嘉等通过分离式霍普金森压杆(SHPB)装置对冷作硬化后的试件进行高应变率(103/s)冲击压缩测试试验表明了低应变率下的冷作硬化可提高钢材抗冲击强度［1］;王艳云等通过对低碳钢材料试件进行拉伸试验，研究了静态条件下低碳钢的有关力学性能［2］，因而钢材等工程材料在高速冲击载荷条件下的变形行为日益受到人们的关注。

本文首先通过静态实验测定CCS-B船用钢材料的静态力学性能参数，然后采用分离式霍普金森压杆(SHPB)实验装置对CCS-B 进行动态力学性能试验研究。基于“三波法”理论，编程计算试件材料的动态力学参数，如应力、应变率时间历程曲线以及试件的平均应力—应变曲线，给出了材料在不同应变率下的本构关系和屈服强度。

1 动态冲击实验

1.1 实验装置

分离式Hopkinson压杆实验装置［3］主要用于测量材料在高应变率下(102～104)/s的动态力学性能。由于该系统简单高效，实验精度较高，因而已经成为目前研究材料动态力学性能最基本的实验装置。本实验基于江苏科技大学力学实验中心的分离式Hopkinson压杆实验装置，如图1所示。

图1 SHPB实验装置图

本实验装置包含共轴安装的撞击杆(即子弹)、输入杆(入射杆)、输出杆(透射杆)和吸收杆以及相关的速度测试系统、超动态应变测试系统。试验过程中，通过测量输入杆上的入射波、反射波与输出杆上透射波信号，推导出试件材料的动态力学性能参数。其系统工作示意图如图2所示。

1.2 实验方案

由于动态实验装置要求试件的尺寸非常小、精度非常高，所以加工时在达到尺寸要求的同时还要尽量满足垂直度、水平度以及端面光洁度。选取3个已加工的Φ14.00 mm×8.0 mm小试件，每个试件在不同的冲击压力下进行实验。为增强其实验结果的可靠性，每个试件在单一的冲击压力作用下重复做3次，取其平均值。实验时在试件和压杆端面涂黄油以降低端面摩擦所带来的实验误差［2，4］。该实验所用的SHPB压杆直径为16 mm，对每个试件进行了在气枪内气压分别为 0.3、0.4、0.5 MPa 的动态冲击实验，其实验相关参数见表1、表2。

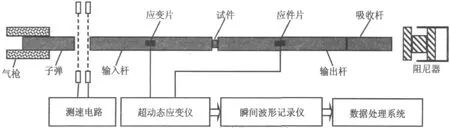
图2 SHPB实验装置原理图

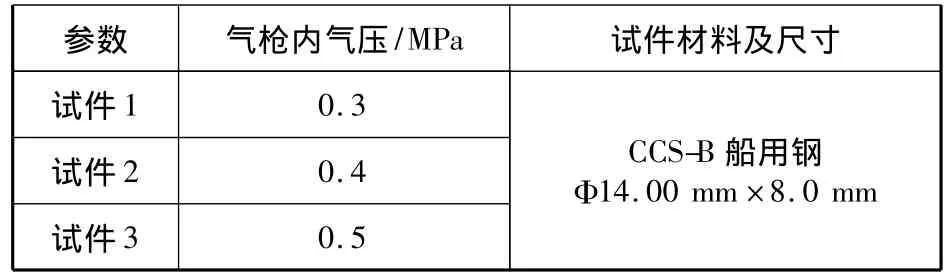
表1 实验方案参数

表2 实验数据参数

1.3 实验数据及现象

超动态应变仪所采集得到的波形数据为应变片的电压信号，如图3所示。

图3 示波器中记录的波形

通过换算公式(1)得到输入、输出杆的应变数据。由于SHPB实验装置中的输入、输出杆一般为高强度钢，因此在冲击过程中仅为弹性变形，通过公式(2)可以得到入射波、反射波和透射波的数据［5］。

式中:ε(t)为SHPB装置中输入输出杆的应变;V(t)为对应的应变片电压信号;σ(t)为应力;k为应变片的灵敏度系数，取k=2.08;E为SHPB装置中杆系材料的弹性模量，取E=200 GPa。

3种不同冲击压力作用下的子弹速度分别为:13.6、15.8、17.9 m/s。图 4、图 5 分别给出了输入、输出杆上应力波形。

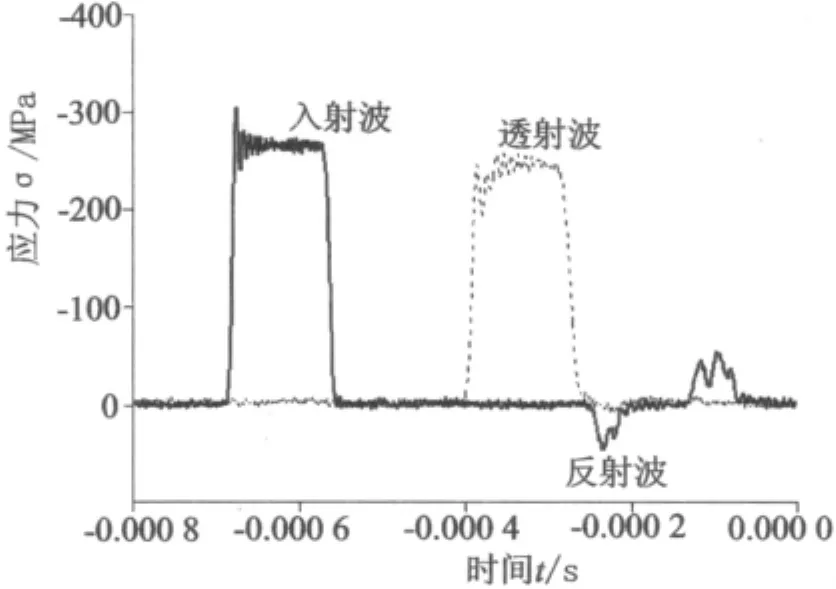
图4 v=13.6 m/s下的入射、反射、透射应力波形图

图5 试件在不同速度下的入射波、反射波应力图

由图4可以看出，反射波与入射波和透射波相比很小，是由于本实验所选择的试件材料和波导杆系的材料相近，因此应力波在界面处发生反射较弱，而大多数的入射波均以透射波的形式传播。

由图5进一步说明，相同尺寸与材料的试件在不同的冲击压力作用下，其波导杆上对应应变片所测得的应变电压信号有着明显的区别。冲击速度越大，其入射波和透射波电压信号越大，即应变信号越大，与常识相符。而在入射脉冲波突然上升后的前端，其观察到波形存在剧烈的振动，作者分析其主要原因为:一是冲击载荷激发杆中的高频响应，其高频信号影响产生强烈振动;二是由于杆的弥散效应而产生。

2 CCS—B动态力学性能分析

根据建立在2个基本假定(即一维假定(又称平面假定)和应力均匀假定)基础上的细长杆弹性应力波传播理论，通过对波导杆上入射、反射和透射应变脉冲的测试，用一维应力波理论分析计算得到试件中的平均应力、平均应变和平均应变率［6］。

平均应力:

式中:c0、E、A分别为Hopkinson压杆装置中的子弹速度、压杆材料的弹性模量以及压杆杆件的横截面面积;A0、l0分别为试件材料的初始横截面积和初始长度;εI、εR和εT分别是试件两端面上入射波、反射波、透射波的应变信号。

应力波在HopKinson压杆和试件中的传播，3个应变波形在时间域上具有比较大的相对差距，各个应变波形的数据点之间却具有内在一一对应的关系，因而准确确定应变波形之间的相对延迟时间和入射波的起点位置成为其数据处理最终结果准确性的重要因素［7］。图6(a)为自编软件中入射波、反射波和透射波的波形起点计算查找结果，图6(b)给出了三波对齐结果。

试件3的应力、应变和应变率随时间变化曲线如图7所示。

对应力和应变数据进行联立，得到试件材料的应力应变历程曲线，其动态载荷作用下冲击速度v=13.6 m/s，v=17.9 m/s 以及静态压缩的应力—应变曲线如图8～图10所示。

由图8～图10可知:在动态冲击实验中，各试件材料在动态冲击载荷作用下，试件材料的屈服强度值随着应变率的增加而增大。过了屈服阶段后，与静态力学性能曲线相比，其强化阶段的强化效果较弱，即强度极限与屈服强度差别不大，并且该材料在动态载荷作用下，当冲击速度v=13.6 m/s时，其屈服强度值比静态大74.643 MPa;当冲击速度v=17.9 m/s时，其值比静态大 247.857 MPa。

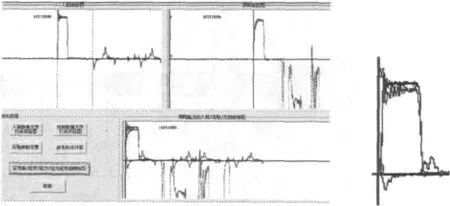
图6 波形起点计算后的电压信号曲线

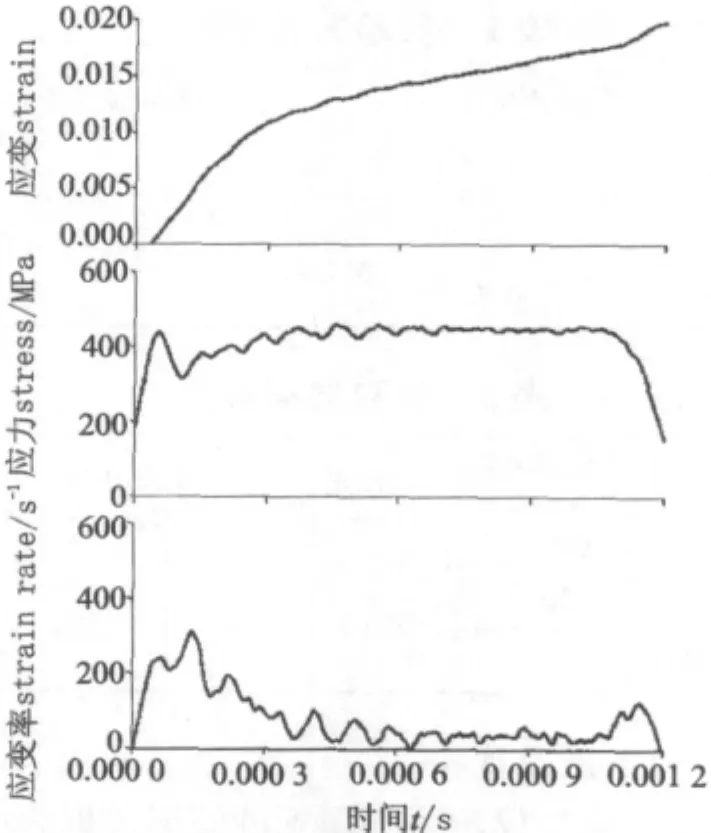
图7 试件3的应力、应变和应变率随时间变化曲线

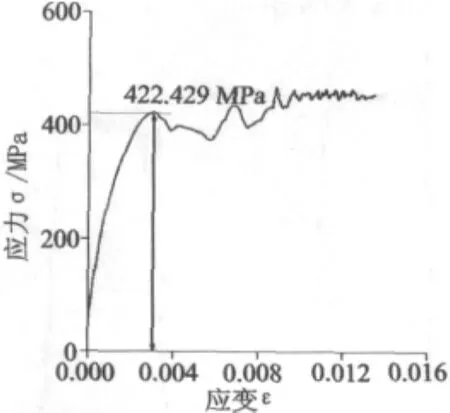
图8 试件1应力—应变曲线(v=13.6 m/s)

图9 试件3应力—应变曲线(v=17.9 m/s)

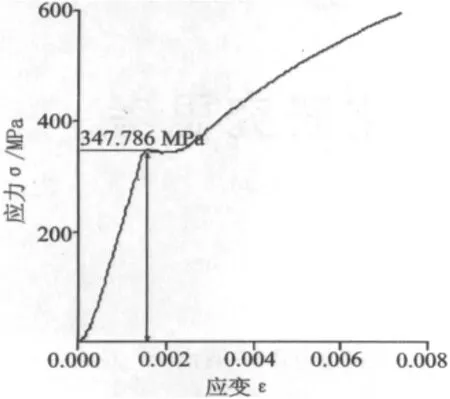
图10 CCS-B船用钢的静态压缩应力—应变曲线

3 结论

(1)用霍普金森压杆实验装置进行材料的动态力学性能测试，必须满足一维理论假设和试件中的应力均匀性假设。一维理论假设由实验设备满足，而应力均匀性假设，需要根据波导杆等进行试件设计时充分考虑试件与波导杆的阻抗匹配，使得应力波经试件透射反射后，已在试件中传播2～3个来回。

(2)试件材料CCS-B船用钢的屈服强度具有应变率敏感性。在不同应变率下，试件材料的动态力学性能测试结果是不同的，表现为应变率相关性，即试件材料的屈服强度值随着应变率的增加而增大。

(3)CCS-B船用钢材料在动态载荷作用下的屈服强度值明显比静态作用下高，而过了屈服阶段后，其强化阶段的强化效果相对静态条件下较弱，即强度极限与屈服强度差别不大。

［1］曲嘉，邹广平，何蕴增.扭转冷作硬化对低碳钢高应变率下后屈服强度的影响［C］//黄风雷，张庆明.第九届全国冲击动力学学术会议论文集(上册).焦作:中国办学学会爆炸力专业委员会，2009:447－451.

［2］王艳云，王庆，陈丽蓉，李娅妮，唐春磊.拉伸速度对低碳钢和铸铁力学性能影响的实验研究［J］.农业与技术，2010，30(6):118－120.

［3］Kolsky H.An investigation of mechanical properties of materials at very high rates of loading［J］.Proc Phys Soc，1949，B62:676 －700.

［4］许泽建.40Cr和30CrMnSiNi2A高应变率动态起裂特性的研究［D］.西安:西北工业大学，2005.

［5］何著，赵寿根，杨嘉陵，程伟.0Cr17Ni4Cu4Nb不锈钢动态力学性能研究［J］.材料科学与工程学报，2007，25(3):418 －421.

［6］龚育宁.弹性应力波理论［M］.南京:华东工学院出版社，1988.

［7］李英雷，胡昌明，王悟.SHPB实验数据处理的规范化问题讨论［J］.爆炸与冲击，2005，25(6):553－558.