商用数码相机透镜畸变校正算法比较
李芳芳,刘华朋
(1.西南交通大学希望学院,四川南充 637900,2.中铁十六局集团路桥工程有限公司,北京 101500)
为实现工程测量与数字近景摄影测量的结合,量测型数码相机应运产生。但量测数码相机价格昂贵,所以宜采用商用的数码相机。即商用量测型数码相机,但其相机的内方位元素(X0,Y0,f)未知,且其镜头畸变对测量的精度影响较大,因此在进行高精度的测量模式作业前需要对相机进行严格的标定[1]。
摄像机的标定是确定摄像机内部参数或外部参数的过程。内部参数是指摄像机内部的几何和光学特性,外参数是指摄像机相对世界坐标系原点的平移和旋转位置。
在检测的视觉系统中,使用广角镜头可以进行大范围测量[2],但短焦距、广角镜头的摄像机系统与理想的小孔透视模型(pin hole model)有一定的差别,从而使得物体点在摄像机图像平面上实际所成的像与理想成像之间存在不同程度的非线性光学畸变[5]。相机镜头的非线性畸变仅与它所选用的焦距有关,与其他的内部参数、外部参数无关。畸变图像不利于计算机视觉进行现场测量和图像处理,必须对图像的非线性畸变进行校正,校正精度直接影响到最终的测量精度。
图像的非线性畸变主要分为两部分:径向畸变和切向畸变。切向畸变较小,影响不大,一般不予考虑,以径向畸变为主。如能预先知道畸变模型,则进行校正后就可应用针孔摄像机模型来进行视觉计算。然而制造商一般不提供镜头的畸变模型,并且批量生产中不可避免的随机性导致同一规格型号镜头的畸变参数也不相同,这就需要有简便的方法来获取镜头的畸变参数。
1 数码图像的非线性畸变
图像的非线性畸变与相机成像过程中的外部参数和光源到镜头的距离无关,仅与光线经过镜头的位置有关。畸变的形成是由于入射光线在通过各个透镜时的折射误差和电荷耦合器件(Charge Couple Device,CCD)点阵位置误差所致。不同的焦距将对应着不同的非线性畸变,因为调焦将引起主点位置(x0,y0)的变化,所以在获取照片的时候要锁定主距,以达到锁定内方位元素值和光学透镜畸变系数的目的[4]。
对一架变焦相机来说,它的非线性畸变特性是随着焦距的变化而变化,选定一种焦距,也就有一个确定的畸变与之对应;定焦相机的非线性畸变特性是固定的。随着CCD 制造技术的发展,CCD 的像素值越来越大,像素点间距也变得越来越小,图像中的非线性畸变在机器视觉的研究中就显得更为重要。非线性畸变的研究成为很多学者研究的内容。姜大志等人[1]提出了把非线性畸变参数的求解独立于相机其他参数求解的方案,可以获得较高精度的畸变参数,为机器视觉技术的应用提供了一种简捷、可靠、实用的新方法,但这要利用专门的实验室装置在实验室中进行。张靖等人[2]采用基于直线的射影变换特点,提出一种校正镜头畸变的非量测算法,用面积平方和定义畸变测度,计算量小且具有抗噪声能力,避免了收敛于局部极小值,但方法复杂;朱汉敏[3]利用畸变的球形模型,基于物方直线特征,实现了畸变的数字校正,整个校正过程不需要其他的光学测量仪器,也不需要知道光学系统的结构参数,只是根据畸变特征进行校正。
在图像坐标系中的非线性畸变包括径向畸变、离心畸变、薄棱镜畸变。若同时考虑这三部分的影响,将因为引入过多的非线性畸变参数而引起解的不稳定[10]。田原嫄以理想针孔成像模型为基础,证明了影响畸变的主要因子是径向畸变,其他因子的影响基本不大,可忽略不计[5],因此在一般应用中仅考虑径向畸变。径向误差是由镜头中各组透镜的表面曲率存在误差引起的,在以径向畸变为主的非线性几何畸变模型中,无畸变像面坐标和畸变像面坐标之间的关系可表示为:

式中:xp、yp为无畸变像平面坐标;xd、yd为畸变像平面坐标,它们的坐标原点都在对称中心;k为径向畸变系数,k>0 表示枕形畸变,k<0 表示桶形畸变。
通过对径向畸变校正算法的研究回顾,发现球形模型算法和多项式算法是运用较多的两个算法,且精度也达到了各自所研究对象的径向畸变校正的要求。为探索哪一种算法满足更高校正精度要求,本文以实验比较这两种算法的精度。
2 实验校正过程
实验使用的相机焦距可调,拍照时采取手动调焦来固定焦距,以得到准确的焦距参数。本实验采用的焦距参数为5.8 mm。
绘制一个等间隔正交方网格,由25 根横向直线和25 根纵向直线组成,纵、横向直线间的距离为5 mm,线长度误差小于7‰,线宽0.07 mm。在相机拍摄时,方格网应能布满成像平面,且使光轴垂直于方格网,光轴尽量通过方格网中心,因此需要一个便于调节的相机支撑装置。
将绘好的正交方格网贴附于平面上,用待校相机照准成像,获得如图1 所示的原始图像。从图可看出网格边沿处明显有畸变,实际存在的物方直线在影像上是一条曲线。
2.1 球形模型校正法
物方一直线段在径向畸变下变为椭圆的一段,椭圆弧可视为标准椭圆中心平移到C(x0,y0)、旋转θ0而得,椭圆的长半轴a 等于球形模型的半径R。文献[5]证明用球形模型表示径向畸变是恰当的,任意一点的位置畸变仅与该点极坐标中的矢径坐标有关,在球形模型下,极坐标公式为:
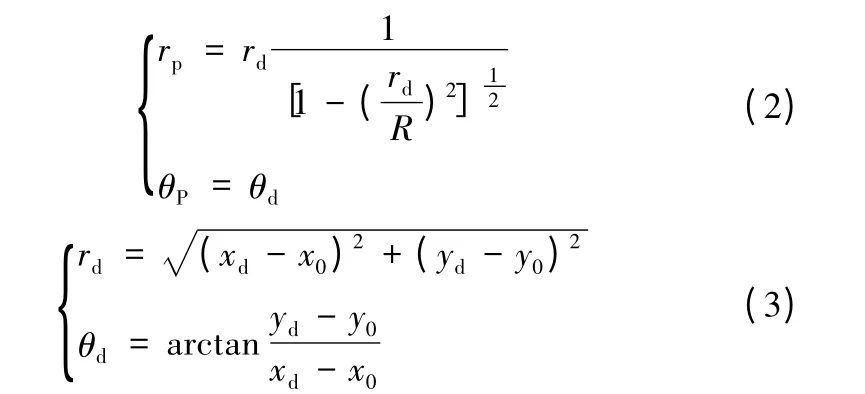
式中:rp、θp为无畸变点的极径和极角;rd、θd畸变点的极径和极角;R为球半径;x0、y0为畸变中心;xp、yp、xd、yd的涵义同式(1)。
校正过程是先对原始图像进行二值化处理和骨架提取,处理出网格交点,获得交点处的数字坐标,然后根据标准特征值分解(Eigen Value Decomposition,EVD)算法和径向畸变下的椭圆弧方程[10],可求得R 和(x0,y0)。这样就可以根据畸变图像中各点的坐标(xd,yd)算得对应的无畸变点(rp,θp),从而校正图像。
原图像像素点变换后坐标一般要改变,若没落在像素点上,此时可用相邻像素点上的灰度值通过插值求出其灰度值,常用的插值算法有最邻近点法、双线性内插法及三次卷积法;最邻近点法算法非常简单并且保持原光谱信息不变,但是几何精度较差;双线性插值法具有计算简单、几何上准确度较高、能克服灰度不连续等优点;三次卷积法计算量较大,但比较准确。综合考虑各个算法的优缺点,实验采用双线性内插法进行插值,经过插值后,可避免校正后图像出现“空”像素的情况。
图2 是纠正了透镜畸变的方格网,从图上可以看出,网格线已全部拉直。
2.2 多项式纠正法
多项式表示的径向畸变模型公式为:


图1 待校正畸变图

图2 球形模型校正结果
式中:aij为多项式的系数;n为多项式的次数。
透镜的径向畸变有均匀畸变和不均匀畸变。曾峦[8]采用的透镜畸变是均匀畸变,校正结果较理想。均匀畸变是不均匀畸变的特殊情况,为了不失一般性,假定实验的透镜畸变为不均匀畸变。在方格网成像后,因为透镜畸变的存在,每一交点的坐标为实际成像坐标。
针对图1 所示的原始图像进行计算,先对该图像进行二值化处理和骨架提取,处理出网格交点,并分别读出各交点的实际成像坐标。视线上的所有物点都成像在像面上同一位置,利用这一特性可以让原方格网的中心和成像后的方格网的成像中心在同一个位置,这样实际成像坐标所对应的理想成像坐标也是知道的,则可以得到每一交点处的径向畸变系数,利用该点的畸变系数及式(4)对图像进行校正,生成的无畸变图像如图3 所示。需要说明的是用多项式法校正和球形模型法校正一样,也需要进行灰度内插。
统计纠正前后网格点(角点)像素坐标的变化可说明图像纠正的精度。原始图像是等间隔正交方网格,像素坐标系的原点在CCD 图像平面的左上角,I 轴、J 轴分别平行于图像坐标系的x 轴和y 轴。在进行残差统计时,使用中误差、平均误差及畸变最大值等统计量,统计结果如表1 所示。

图3 多项式校正结果
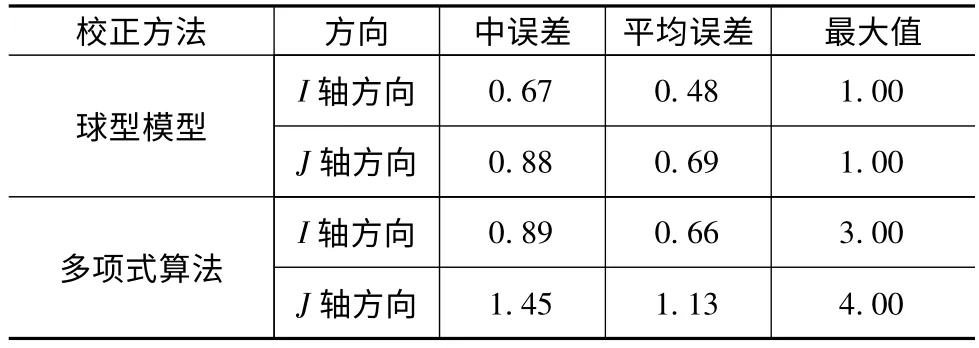
表1 图像校正后格网角点像素坐标与标准像素坐标的残差统计结果(像素)
从表1可以看出,无论是I 轴方向还是J 轴方向,球形模型校正的误差均小于多项式算法校正的误差。还可以看出,无论是球形模型校正还是多项式算法校正,纵向(J 轴)的误差均大于横向(I 轴)的误差,这是因为纵向为相机拍摄方向,照片产生几何变形主要是由纵向失真引起。因本论文图像的像素间距为0.064 mm,可知球型模型校正的I 轴方向中误差为0.04 mm,平均误差为0.03 mm,最大误差为0.064 mm,J 轴方向中误差为0.06 mm,平均误差为0.05 mm,最大误差为0.064 mm。
3 结 论
采用球形模型和多项式两种算法对数码影像进行畸变校正处理,校正结果无论从直观上还是量化数据上,都可以得出球形模型的校正精度比多项式校正精度高。除此之外,球形模型校正算法简单,实用性也好,可以得出球型模型校正的精度可以满足更高畸变校正要求的结论。
[1]姜大志.标准图形法求解相机镜头非线性畸变的研究[J].东南大学学报,2001,31(4)
[2]张靖.摄像机镜头畸变的一种非量测校正方法[J].光学学报,2008,28(8)
[3]朱汉敏.基于直线特征的径向畸变图像的校正[J].上海工程技术大学学报,2006,20(2):154-155
[4[ 崔红霞.非量测数码相机的畸变差检测研究[J].测绘科学,2005,30(1)
[5]田原嫄.基于CCD 摄像机成像的径向畸变研究[J].世界科技研究与发展,2008,30(2)
[6]Tsai R Y.A versatile camera calibration technique for high-accuracy 3D machine vision[J].International Journal of Robotics and Automation,1987,3(4):323-344
[7]冯文灏.数码相机实施摄影测量的几个问题[J].测绘信息与工程,2002,27(3)
[8]曾峦.短焦距摄像机镜头的畸变校正方法[J].装备指挥技术学院学报,2002,13(2):53-55
[9]郑莹.铁路轨道数码影像的纠正与拼接[D].西南交通大学,2008
[10]田涌涛.基于共线点的透镜畸变系数标定[J].上海交通大学学报,2003,37(11)

