基于MATLAB 的压杆稳定性分析
刘明超,李 慧,刘俊杰
(1.山东大学土建与水利学院,山东济南 250002;2.北京理工大学宇航学院,北京 100081)
压杆稳定性分析是工程实践中的常见问题。为了保证机构安全可靠地工作,必须使压杆处于直线平衡状态,如果将压杆的工作载荷控制在临界载荷允许的范围内,则压杆就不会失稳。由此可见,临界载荷的确定对于压杆稳定性的分析是非常重要的。
在实际分析压杆稳定性的问题中,临界载荷的确定通常采用手工计算的方法,往往比较繁琐。本文在经典稳定性理论的基础上将计算过程系统化、公式化,绘出了流程图,并编写了压杆稳定性分析的MATLAB 程序,与手工计算相比,更加方便实用。
1 经典稳定性理论
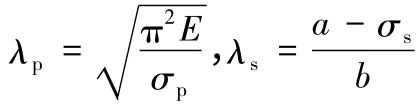
1.1 大柔度压杆临界应力(欧拉)公式
对于满足λ≥λp的压杆,就称之为大柔度压杆,也即细长压杆。其在失稳时处于线弹性范围(即弹性压杆),临界应力计算可采用欧拉公式:

式中:λ为压杆的柔度。
1.2 中柔度压杆临界应力经验公式
对于满足λs≤λ≤λp的压杆,称为中柔度压杆。其失稳时横截面上的应力超过了材料的比例极限σp,但未超过屈服极限,材料仍满足非线弹性应力应变关系,压杆将发生非线弹性失稳。
对中柔度压杆,临界应力的计算公式是以实验结果为依据归纳出的经验公式,常用如下直线公式:
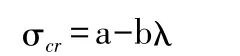
式中:λ为压杆的柔度;a、b 均为材料常数,可查表得出。
1.3 小柔度压杆临界应力公式
对于满足λ<λs的压杆,称为小柔度压杆。其失稳时横截面上的应力理论上超出了σs,故其不会发生失稳,它的破坏是由于轴向压缩的强度不够造成的。故应由轴向压缩的强度条件控制其轴向应力,即:
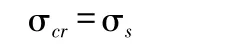
注:对于脆性材料,可将式中σs换为σp。
2 稳定性分析的程序设计
2.1 程序流程图
绘制程序流程图如图1 所示。
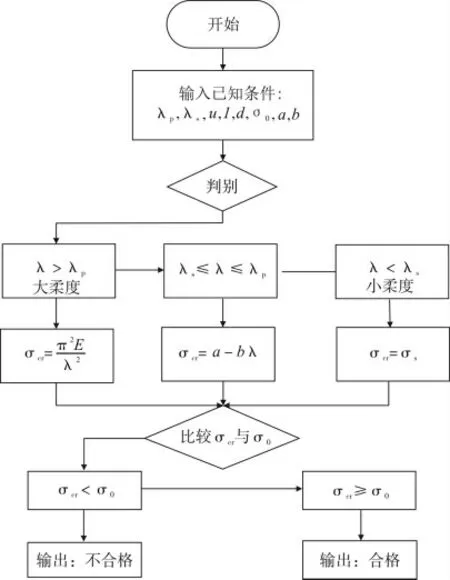
图1 压杆稳定性分析程序流程
2.2 MATLAB 程序
程序采用可视化界面操作,操作界面如图2 所示。

图2 程序操作界面
3 算例验证
图示结构中,AC为刚性梁,BD为直径d=24 mm 的圆截面杆,弹性模量E=200 GPa,λp=100,λs=60,中柔度压杆临界应力经验公式为σcr=(304-1.12λ)MPa,已知s=1 m,l=0.5 m,F=5 kN,试校核该结构的稳定性是否合格。
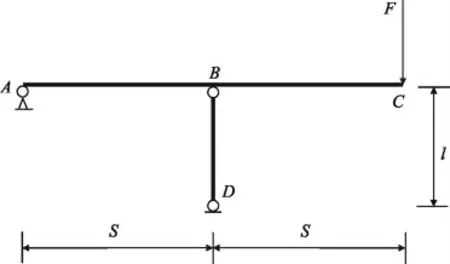
图3 结构计算简图
受力分析,得BD 杆为压杆,压力为:
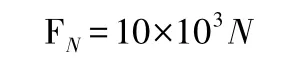
该题目中BD 杆为压杆,校核其稳定性,根据受力分析结果输入参数,运行MATLAB 程序,分析结果如图4 所示。

图4 稳定性分析结果
由程序分析所得结果可知,该压杆稳定性合格。
4 结束语
通过以上理论分析和算例验证我们发现,利用计算机和MATLAB 软件进行结构稳定性分析方便实用,很大程度上提高了工作效率。同时,本文只给出了分析圆截面杆的程序,按照同样的思路稍作修改即可推广到其他规则截面。
[1]刘鸿文.材料力学Ⅰ[M].北京:高等教育出版社,2004
[2]韩斌,刘海燕.材料力学[M].北京:兵器工业出版社,2009
[3]陈家骏.关于细长压杆稳定性问题的讨论[J].力学与实践,1997,19(5):65-67
[4]于洪,刘一华.压杆稳定的机理性认识[J].力学与实践,1991,13(5):57-59
[5]刘延柱.压杆失稳与Liapunov 稳定性[J].力学与实践,2002,24(4):56-59
[6]李彤,李银山.压杆稳定设计的直接迭代法[J].机械设计与研究,2009,25(6):50-53

