石龙山隧道爆破振动信号的小波分析
刘 洋,赵明阶,贺林林,林军志
(1.重庆交通大学水利水运工程教育部重点实验室,重庆400074;2.水利部岩土力学与工程重点实验室 重庆岩基研究中心,重庆400014;3.天津大学 建筑工程学院,天津300072)
石龙山隧道工程为重庆市涪陵区李渡长江大桥南引道道路工程的重要组成部分,位于主线里程K0+260~K1+895 m处。隧道分为左右两线,隧道轴线间距35.5 m,各长约1 635 m。隧道属于城市公路长隧道。隧道内轮廓采用曲墙三心圆断面形式,单洞内净空:宽10.8 m、净高6.8 m,从进口到出口为上坡隧道,沿轴线穿越一条南北向的“条形山脊”,局部呈陡坎状,斜坡、农田分布广泛,有三湾大塘分布,地面高程240~395 m。K0+280~K0+520 m为坡度15°的斜坡地形,K0+520~K1+600 m段地形平缓,K1+600~K1+895 m段地形较陡,平均坡度为27°。隧道围岩为砂岩、泥岩互层,砂岩有利地下水赋存,为含水层或透水层,泥岩不利地下水赋存,为微水层或隔水层。拟建区内无滑坡、泥石流等不良现象,地下水对混凝土无侵蚀。
石龙山隧道分两期实施,施工前一期工程的右线隧道已竣工并投入运营。左线隧道采用钻爆法施工,为了调整左线隧道的爆破参数使其对右线隧道的振动损伤控制在合理的范围之内,有必要对右线隧道测得的爆破振动信号进行全面的分析。
1 爆破振动信号的小波分析原理
小波变换是一种信号的时间-尺度(时间-频率)分析方法,它具有多分辨率的特点,而且在时频两域都具有表征信号局部特征的能力,是一种窗口大小固定不变但其形状可改变,时间窗和频率窗都可以改变的时频局部化分析方法,即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率[1-3]。小波变化的特性满足了对爆破振动信号这种多刻度特征信号进行时频定位的要求,适合爆破振动信号的分析。小波分析得到的信号的频带是按指数等间隔划分的,若设被分解信号的频率范围为(0,W),则其经第1层分解后被分成低频a1(0,W/2)和高频d1(W/2,W)两部分;第2层小波分解则是对第1层分解后的低频部分a1(0,W/2)进行进一步分解,得到低频a2(0,W/4)和高频d2(W/4,W/2)两部分;以此类推,分解n次(尺度为n)即可得到n层的小波分析结果。
将被分析信号分解到第n层,设Sj对应的能量为Ej,则有:

式中:xi,j表示重构信号的离散点幅值。设被分析信号的总能量为E0,则有:

各频带的相对能量分布为[4-7]:

2 爆破振动信号的小波分析
2.1 小波尺度分解
针对不同的爆破参数(表1),在先行洞(右线隧道)底板靠近后行洞(左线隧道)爆破面边墙处布设垂直、水平切向和水平径向3个检波器。

表1 某炮次的爆破参数Table 1 Blasting parameters of one blasting
为保证相同的爆破条件,将同一炮次垂直向、水平切向和水平径向测得的爆破振动信号采用多分辨率小波分析技术进行处理。由于Inrid Daubechies小波系列具有较好的紧支撑性、光滑性及近似对称性,故对采集的爆破振动信号进行小波分析时,选择db8作为小波基函数。分解层数取决于具体信号特征及采用的速度传感器的工作频率而定。本次设置的信号采样频率为 5 000 Hz,根据采样定理[8-10],则其奈奎斯特(Nyquist)频率为5 000/2=2 500 Hz。根据分析需要,对各测点爆破振动信号进行尺度为7的小波分解和重构,则7个小波分解层析所对应的8个频带的取值分别为:0 ~19.531 25,19.531 25 ~39.062 5,39.062 5 ~78.125,78.125 ~156.25,156.25 ~312.5,312.5 ~625,625 ~1 250,1 250 ~2 500 Hz。
2.2 幅值特性
根据表1的爆破参数,所测得的水平切向爆破振动信号,及经小波分解后的重构信号如图1。图2、图3分别为垂直向及水平径向的原始信号及小波分解后的重构信号。图4为水平切向的原始爆破振动信号进行7层小波分解后所对应的各层小波分解信号。
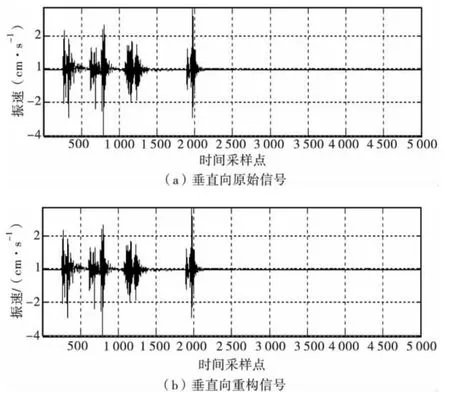
图2 垂直向信号Fig.2 Vertical signal
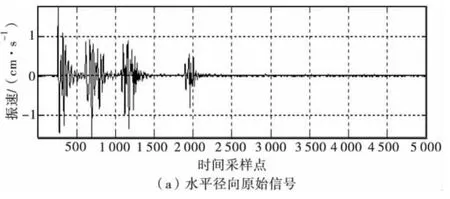
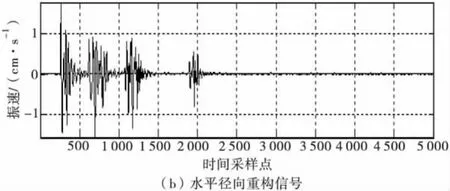
图3 水平径向信号Fig.3 Horizontal radial signal

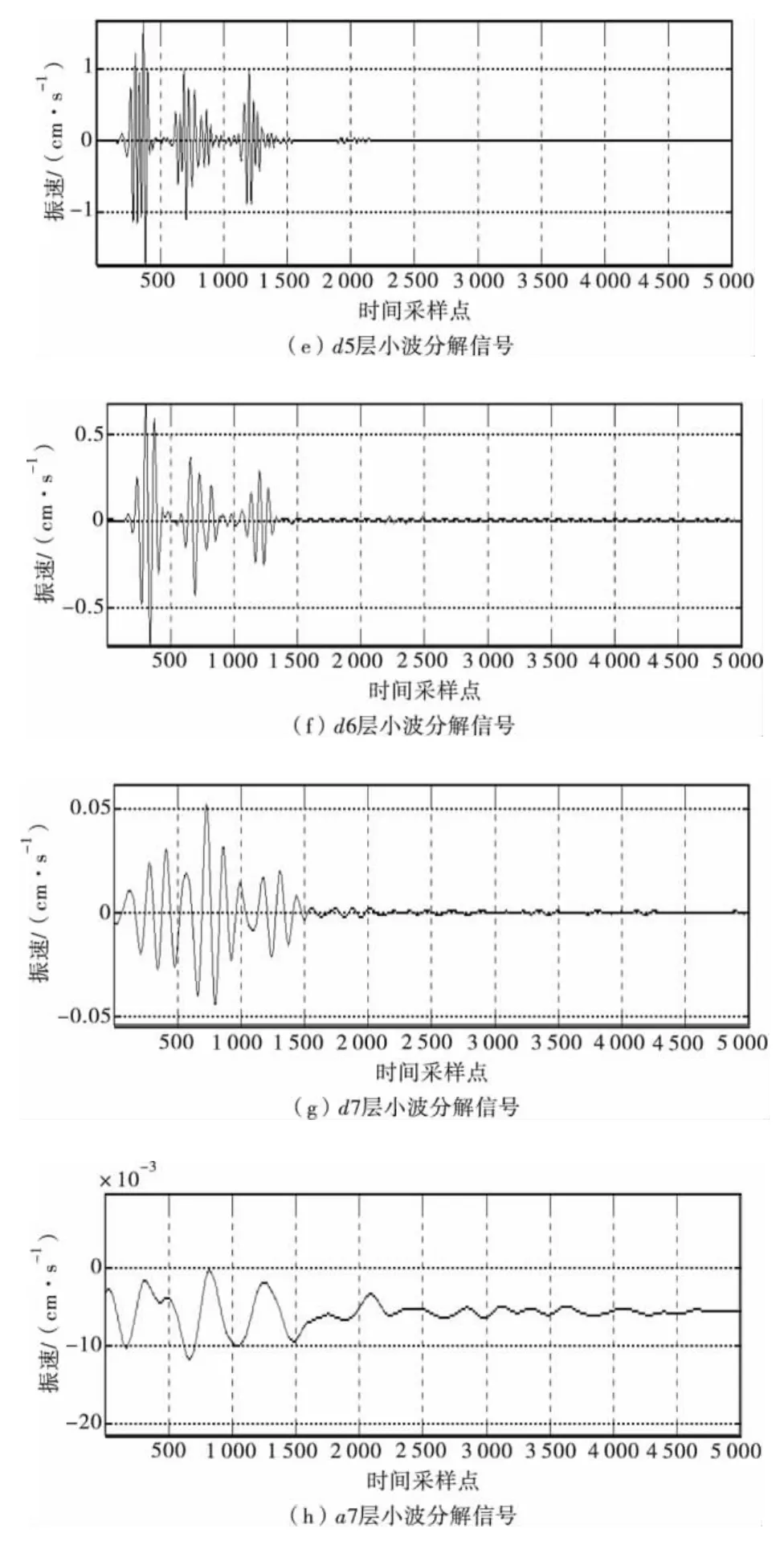
图4 基于db8小波基的小波分析Fig.4 Wavelet analysis based on db8 wavelet basis function
根据各层小波的分解信号得到各层小波的最大振速见表2。

表2 各方向各层小波质点最大振速Table 2 The maximum particle velocity of each layer of wavelet in different directions
由表2可以看出,垂直向的最大振速为4.04 cm/s,大于水平切向的2.37 cm/s,大于水平径向的1.78 cm/s。水平切向各层小波中最大振速出现在d5层小波上,为1.238 cm/s;垂直向各层小波中最大振速出现在d1层小波上,为2.657 cm/s;水平径向各层小波最大振速出现在d4层小波上,为 1.239 cm/s。
2.3 频谱特性
运用MATLAB程序对原始信号及分解得到的各层小波进行计算得到的水平切向原始信号功率谱见图5,d1~a7层小波的功率谱见图6。

图5 水平切向原始信号功率谱Fig.5 Power spectrum of horizontal tangential original signal
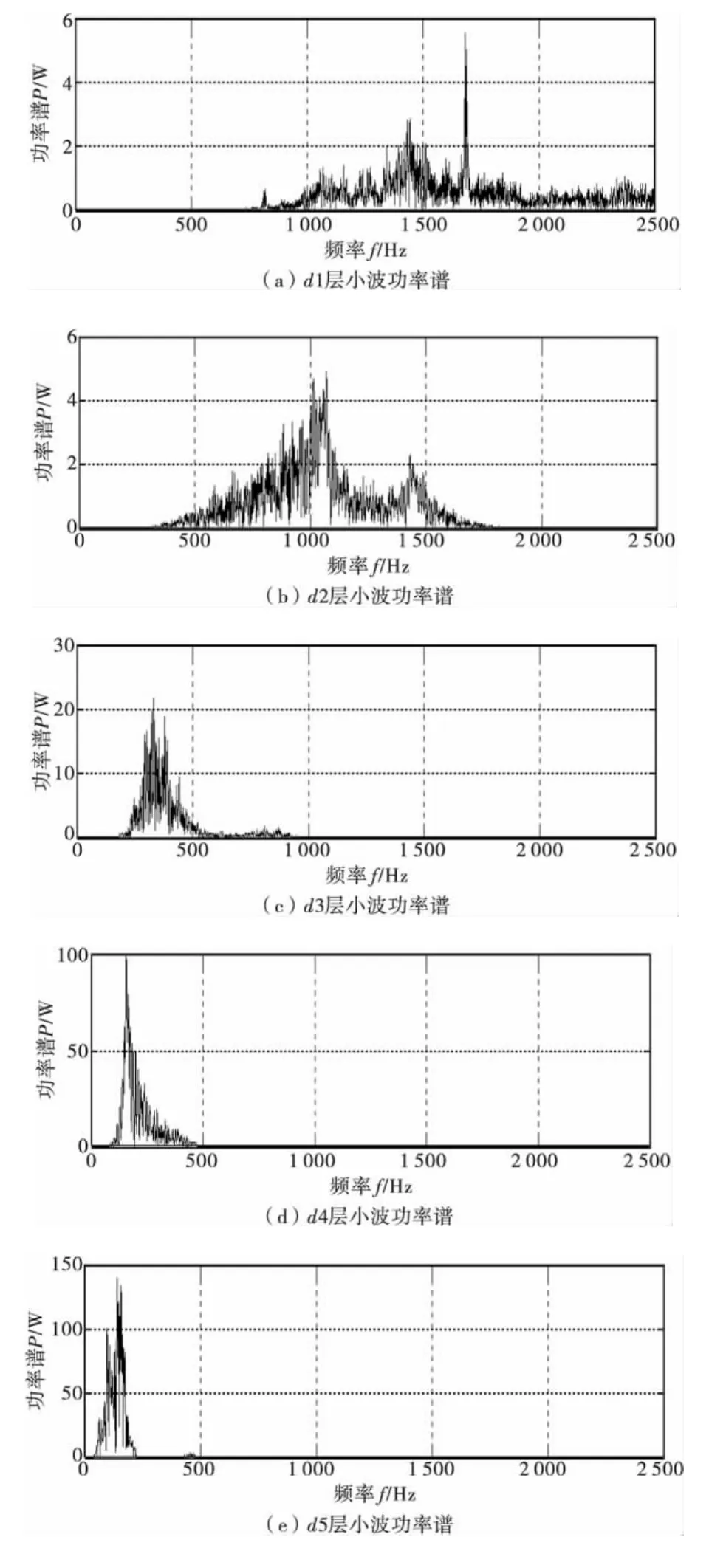

图6 各小波分量的功率谱Fig.6 Power spectrum of each layer
由图5原始信号及图6各层小波的功率谱可以看出:
1)该爆破振动信号的能量带分布很宽,且各方向的优势频率大致在相同的范围内。水平切向的频率主要分布在 39.062 5~312.5 Hz频率段,即39.062 5~312.5 Hz是水平切向的优势频率;垂直向和水平径向的优势频率分别为78.125~2 500 Hz和39.062 5 ~625 Hz。
2)垂直方向的主频为352 Hz,大于水平径向的主频155 Hz,大于水平切向的主频139 Hz。
2.4 能量分布特性
根据式(1)~式(3)编写MATLAB计算程序,运行后得到不同频域的能量所占比例[11-12],将各层小波的主频及能力比例进行统计,结果见表3。
由各层小波的频谱参数可以看出:①对于水平切向原始信号而言,其能量主要集中在d4、d5及d6层小波上,这3层小波占总能量的97.61%,其余5层小波均为干扰成分。该信号的主频为139 Hz,在d5层小波78.125~156.25 Hz频带范围之内,而 d5层小波在各层小波中所占能量比例最大,两者是相互吻合的;②对于垂直向原始信号而言,其能量主要集中在d1、d2、d3、d4及d5层小波上,这5层小波占总能量的98.79%,其余3层小波均为干扰成分。该信号的主频为352 Hz,在d3层小波312.5 ~625 Hz频带范围之内,而d3层小波在各层小波中所占能量比例最大,两者是相互吻合的;③对于水平径向原始信号而言,其能量主要集中在d3、d4、d5及d6层小波上,这4层小波占总能量的98.46%,其余4层小波均为干扰成分。该信号的主频为155 Hz,在d5层小波78.125 ~156.25 Hz频带范围之内,而d5层小波在各层小波中所占能量比例最大,两者是相互吻合的。

表3 各层小波的频谱参数Table 3 Spectrum parameters of each layer of wavelet
3 结论
选用db8作为小波基函数,对石龙山隧道同一炮次下垂直向、水平切向、水平径向的爆破振动信号进行了尺度为7的小波分解和重构,得到以下结论:
1)水平切向在0 ~39.062 5 Hz频带和312.5~2 500 Hz频带范围内均为干扰信号;垂直向在0~78.125 Hz频带范围内均为干扰信号;水平径向在0~39.062 5 Hz频带和625 ~2 500 Hz频带范围内均为干扰信号。
2)水平切向、垂直向和水平径向的主频分别在d5层、d3层和d5层的小波频带范围之内,而上述几层小波均是所在小波尺度内能量最大的小波,这充分表明本次小波分解的真实性和可靠性。
3)小波分析是更深入全面地了解爆破振动信号的一种有效的方法,尤其是根据小波分析得到的优势频率,与被监测建筑物或者构筑物的固有频率进行比对,通过对爆破参数的合理调整,可以避免两者频率相近所带来的共振效应。这是除了质点振动速度这一爆破安全指标之外的又一非常重要的安全控制指标。
[1]赵明阶,叶晓明,吴德伦.工程爆破振动信号分析中的小波方法[J].重庆交通学院学报,1999,18(3):35 -41.Zhao Mingjie,Ye Xiaoming,Wu Delun.The wavelet-fourier analysis of blasting seismic signal[J].Journal of Chongqing Jiaotong U-niversity,1999,18(3):35-41.
[2]何军,于亚伦,梁文基.爆破振动信号的小波分析[J].岩土工程学报,1998,20(1):47 -50.He Jun,Yu Yalun,Liang Wenji.Wavelet analysis for blasting seismic signals[J].Chinese Journal of Geotechnical Engineering,1998,20(1):47- 50.
[3]林从谋,杨林德,崔积弘.浅埋隧道掘进爆破振动特征研究[J].地下空间与工程学报,2006,2(2):276 -279.Lin Congmou,Yang Linde,Cui Jihong.Study on the vibration characteristic of the shallow-tunneling blasting[J].Chinese Journal of Underground Space and Engineering,2006,2(2):276-279.
[4]李金龙.小波变化方法及其应用[J].地震,2001,21(3):91 -97.Li Jinlong.Wavelet transform method and its application [J].Earthquake,2001,21(3):91-97.
[5]刘敦文,粟闯,龚运高.一种基于爆破振动信号小波分析的爆破危害评判新方法[J].中南大学学报:自然科学版,2010,41(4):1574-1577.Liu Dunwen,Su Chuang,Gong Yungao.New method for blasting hazards evaluation based on wavelet analysis of blasting vibration signals[J].Journal of Central South University:Science and Technology,2010,41(4):1574-1577.
[6]林大超,施惠基,白春华,等.爆炸地震效应的时频分析[J].爆炸与冲击,2003,23(1):31 -35.Lin Dachao,Shi Huji,Bai Chunhua,et al.Time-frequency analysis of explosion seismic effects[J].Explosion and Shock Waves,2003,23(1):31-35.
[7]娄建武,龙源,徐全军.小波分析在结构物对爆破振动响应的能量分析法中的应用[J].世界地震工程,2001,17(1):64 -66.Lou Jianwu,Long Yuan,Xu Quanjun.Study on the wavelet analysis applied in structure response to blasting vibration[J].World Information on Earthquake Engineering,2001,17(1):64-66.
[8]钟祖良,刘新荣,梁宁慧,等.质点振动速度与主振频率在爆破监测中的应用[J].重庆建筑大学学报,2006,28(4):38 -41.Zhong Zuliang,Liu Xinrong,Liang Ninghui,et al.Discussion on application of the peak particle velocity and main vibration frequency in blast vibration monitoring[J].Journal of Chongqing Jianzhu University,2006,28(4):38-41.
[9]凌同华,李夕兵.爆破振动信号不同领域的能力分布规律[J].中南大学学报:自然科学版,2004,35(2):310-312.Ling Tonghua,Li Xibing.Laws of energy distribution in different frequency bands for blast vibration signals[J].Journal of Central South University:Natural Science,2004,35(2):310 -312.
[10]徐学勇,冯谦,雷静雅.基于小波包变换的爆破震动信号能量分析方法[J].大地测量与地球动力学,2010,30(增刊2):27-30.Xu Xueyong,Feng Qian,Lei Jingya.Energy analysis method based on wavelet packet transformation for explosion vibration signal[J]. Journal of Geodesy and Geodynamics,2010,30(supp2):27-30.
[11]徐国元,中国生,熊正明.基于小波变换的爆破地震安全能量分析法的应用研究[J].岩土工程学报,2006,28(1):24 -27.Xu Guoyuan,Zhong Guosheng,Xiong Zhengming.Study and application of energy analysis method for blasting seismic safety based on wavelet transform[J].Chinese Journal of Geotechnical Engineering,2006,28(1):24-27.
[12]陈士海,魏海霞,张子华,等.钢筋混凝土结构爆破地震响应频谱及幅值变化规律分析[J].振动与冲击,2011,30(1):213-217.Chen Shihai,Wei Haixia,Zhang Zihua et al.Spectral analysis and amplitude varying for blasting vibration response of a reinforced concrete building[J].Journal of Vibration and Shock,2011,30(1):213- 217.

