双星定位系统定位精度的Cramer-Rao下界分析✴

严航，姚山峰

双星定位系统定位精度的Cramer-Rao下界分析✴

严航，姚山峰

（盲信号处理国防科技重点实验室，成都610041）

介绍了双星时频差定位原理，在此基础上研究了在地球表面约束条件下的双星定位系统的定位精度理论下界。利用推导的定位精度Cramer-Rao下界，仿真分析了定位参数估计精度、卫星星历、目标辐射源位置以及辐射源载波频率等因素对定位精度的影响，并给出了物理解释。定位仿真试验结果表明，定位精度变化趋势与Cramer-Rao下界一致，证明了理论推导的正确性。

双星定位；时频差；参数测量误差；定位误差；Cramer-Rao下界

1 引言

随着卫星通信的迅速发展，地面辐射源对卫星的有意或无意干扰日益增加，影响了通信卫星的正常运行。对干扰进行处理，必须首先确定干扰发射机的位置。美、英、法等国都对卫星干扰源定位问题展开了研究，并取得了相应成果［1-3］，成功地研制出卫星干扰源定位系统，如TLS2000系统、SatlD系统以及HyperLoc系统。卫星受干扰事件暴露了卫星安全方面存在的隐患，卫星干扰源定位问题已成为当前卫星通信系统抗干扰的一项新的重要内容，国内对该问题的研究正在兴起。同时，卫星上行信号辐射源定位在军事上也具有重要的意义［4-5］。

按照定位原理的不同，对地面辐射源的定位可以分为两大类：第一类采用空中／空间平台作为定位设备载体。对于高轨或者同步卫星，通常采用星载的阵列天线，利用方向图变化特性进行定位。对于低轨卫星或者飞机等快速移动平台，通常采用接收频率的多普勒效应，形成测量轨迹。第二类主要利用地面平台进行处理，卫星只是进行简单的信号转发。对于合作用户的定位，可以通过伪码测距与测时差结合的方法，获得几十米的定位精度，如GPS定位系统和我国自行研制的“北斗”导航定位系统。对于非法用户和干扰辐射源，则通常利用双星体制形成的到达时间差和多普勒频率差进行定位。

在双星定位方面，国外起步较早，先后开展了利用连续波信号和调制信号的到达信号多普勒频差（Differential Frequency Offset，DFO）和到达时间差（Differential Time Offset，DTO）定位技术研究，D.P.Haworth等分析设计了系统模型与框架，最终采用了时差／频差组合定位体制，并通过引入参考信号提高定位精度［2］。K.C.Ho和Y.T.Chan等人长期以来从事辐射源时差、时差／频差定位的原理研究，推导了一种迭代算法和方程的线性化方法，使得在一些定位问题中，能避免发散和计算量大的弊端［3］。本文主要对双星时频差定位体制的卫星上行信号辐射源定位系统进行研究，分析定位参数测量误差与定位误差之间的传递关系，推导分析出定位精度的Cramer-Rao下界（Cramer-Rao Lower Bound，CRLB）。

2 定位原理

图1给出了双星定位的原理示意图。双星定位系统实现对地面卫星上行辐射源定位利用了两颗在空间彼此靠近的同步卫星，其中目标辐射源通信利用的卫星称之为主星，在主星邻近位置用于辅助定位的卫星称之为邻近星。由于发射机的天线特性，波束主瓣对准主星，而波束副瓣则指向邻近星。

图1 双星定位原理示意图Fig.1 Dual-satellite geolocation principle

由于主星和邻星处于不同的位置，因此地面站接收到的两颗卫星的转发信号有不同的时延，形成到达时间差DTO；同时，由于两颗同步卫星的漂移存在一定的运动速度，卫星速度矢量在目标源与地面接收站之间的径向方向上的投影不同，形成多普勒频差DFO。设地面站接收的主星信号、邻星信号分别为s1（t）、s2（t）。由于两路信号为同源信号，因此利用互模糊函数

可以实现对时差参数τ（DTO）以及多普勒频差参数fd（DFO）的无偏估计［6-7］。

利用时频差定位参数估计值，根据图1中的几何关系可以建立定位方程：

式中，r、rm1、rm2是目标辐射源和主星、邻星接收站在地心坐标系中的位置矢量，rs1、rs2是主星、邻星在地心坐标系中的位置矢量，c是光速，fu是目标信号源的信号频率，Dto、Dfo是目标辐射源对两颗卫星的时间差和频率差，vs1、vs2是主星和邻星的速度矢量，ui是从目标辐射源到卫星位置矢量rsi的单位矢量，u1（rm1）和u2（rm2）是接收站位置矢量rm1、rm2分别到卫星位置矢量rs1、rs2的单位矢量。

在式（2）和式（3）中，从卫星到地面接收站的距离差和频率差可以根据星历计算，因此可以只使用上行链路的斜距差（DSR）和斜距差的变化率（DSRR）来表示［1-2，8］。式（2）和式（3）可简化为

对于确定的卫星星历，由某一个Dto，uplink值确定的轨迹是一个双曲面，与地球面可相交出一条曲线，称之为时差位置线（DTO-LOP）；与Dto，uplink类似，Dfo，uplink测量的结果也可以在地球上画出一条位置线，称之为频差位置线（DFO-LOP），由两条位置线（Line of Position，LOP）的交点可以确定目标辐射源的位置，如图2所示。

图2 时差及频差位置曲线示意图Fig.2 Intersection of LOPs

3 定位精度的CRLB分析

任意无偏估计量的估计误差方差即均方误差（MSE）都不能低于某个下界，这就是Cramer-Rao下界（CRLB）。它是根据信息论准则确定的，与估计方法没有关系。对于一般高斯情况下的CRLB以及矢量变换的CRLB有以下结论。

引理1一般高斯情况下的CRLB［9］

假设x～N（μ（θ），C（θ）），则关于θ的Fisher信息矩阵

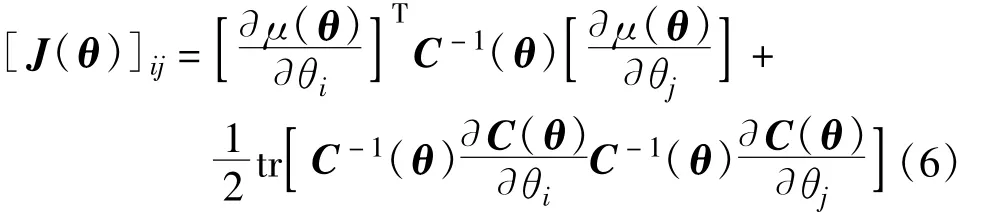
引理1推论当C（θ）与估计参数矢量θ无关时，则关于θ的Fisher信息矩阵可以简化为

引理2矢量参数变换的CRLB［9］

设估计矢量α=g（θ），则α的无偏估计值＾α的协方差矩阵满足

为了公式推导方便，本文首先对一些物理量进行定义和描述。设定位参数矢量为θ，其表达形式如下：

式中，Dto是时差的无偏估计，服从均值为D0to、方差为σ2Dto的高斯分布；Dfo是频差的无偏估计，服从均值为D0fo，方差为σ2Dfo的高斯分布。两者相互独立，则θ～N（θ0，Q）。其中

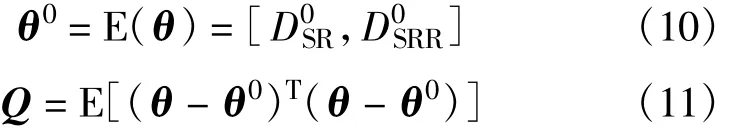
设p（θ；r）是以目标位置矢量（估计矢量）r= [xyz]T为条件的似然函数，其表达式如下：

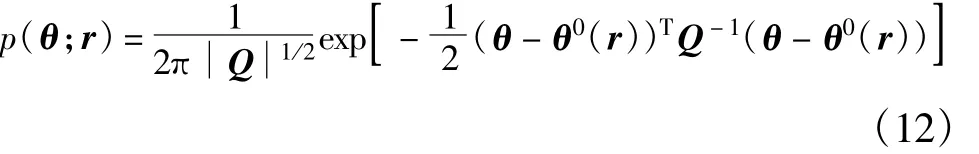
由于目标辐射源在地球表面，因此本问题实质为约束条件下的Cramer-Rao下界的推导分析。定义矢量r1=[xy]T，r=[xyz]T= [r1z（r1）]T，由地球表面方程rTr=R2可以得到z（r1），并且满足下列关系：

将z（r1）代入式（12）可以得到以r1为条件的似然函数，其表达式如下：

由引理1推论，利用式（14），可以计算得到关于估计矢量r1的Fisher信息矩阵

其中：

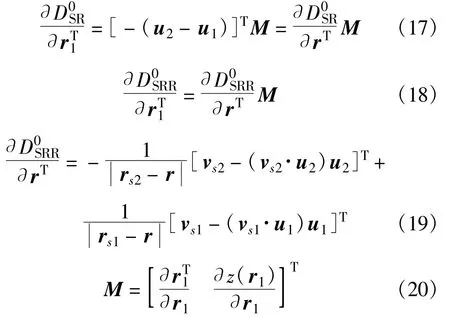
将式（16）、（17）以及（18）代入式（15）中，可以得到J（r1）的表达式：国外学者给出的定位误差分析，通过近似处理的方法忽略了径向误差，具有一定的合理性，但从理论角度分析不够严谨与全面。

由于r=g（r1）=[r1Tz（r1）]T，则根据引理2可以得到r关于r1的雅克比矩阵，其表达式如下：

由引理2结论，可以推出r估计值＾r的协方差矩阵满足

式中，矩阵C表达式如下：

图3 定位精度随星历变化的趋势Fig.3 Relationship between location error and ephemerides

式中，Juc（r）为非约束条件下的Fisher信息矩阵，其表达式如下：

由引理2及矩阵C可以得到估计量＾r在直角坐标系3个方向上估计量的CRLB，其分别为矩阵C的3个对角元素。估计量＾r的最小均方误差为MSE（＾r）min=tr（C）。通过坐标变换矩阵以及矢量参数变换的CRLB定理，可以得到目标辐射源在径向、东西方向以及南北方向的定位精度CRLB。

4 仿真实验与分析

在理论推导的基础上，利用某两颗卫星的真实星历（24 h星历，两个星历之间的时间间隔为1 min），仿真分析卫星星历变化、定位参数估计精度变化以及目标辐射源位置变化对定位精度的影响。

在辐射源位置不变，时差估计精度为5μs，频差估计精度为10 mHz条件下，图3给出了随星历改变（定位时刻改变），在目标辐射源所处地理位置的东西方向、南北方向以及径向方向上的定位精度CRLB的变化趋势仿真分析图。仿真结果表明，不同的星历参数下，定位精度的CRLB变化明显，并存在最大峰，我们称之为定位盲时，并且定位误差主要来源于东西与南北方向的误差，径向定位误差相对很小。

图4和图5是在星历参数确定（某一定位时刻）条件下，给出定位参数估计精度对定位精度CRLB在东西及南北方向分量的影响。图4中时差估计精度为5μs，频差估计精度在5～200 mHz范围变化。可以从图中分析出频差估计精度对南北方向的定位精度的影响大于东西方向。图5中频差估计精度50 mHz，时差估计精度在1～50μs范围变化，同样可以分析出时差估计精度对东西方向的定位精度的影响大于南北方向。这是因为频差曲线基本是东西走向（参照图2），因此随着频差估计精度的改变，频差位置曲线会在真实频差位置曲线作南北方向近似平移，即在时差估计精度确定的情况下（即时差位置曲线固定）频差估计精度对南北方向的定位精度影响较大；时差位置曲线与之相反，因此时差估计精度对东西方向的定位精度影响较大。

图4 频差估计精度对定位精度的影响Fig.4 Relationship between DFO estimation accuracy and location accuracy

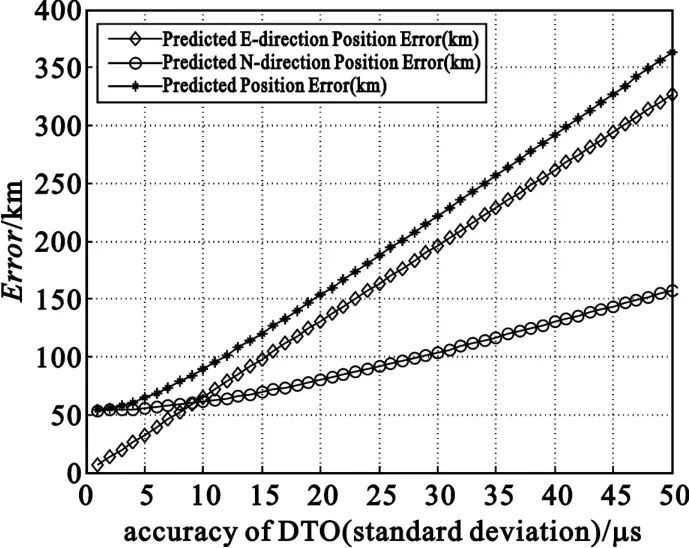
图5 时差估计精度对定位精度的影响Fig.5 Relationship between DFO estimation accuracy and location accuracy

在卫星星历以及定位参数估计精度确定的条件下，图6给出对不同位置的辐射源进行定位的定位精度CRLB。从图6可以分析出，辐射源所处地理位置对定位精度的影响很大，其本质是GDOP的改变造成对定位精度的影响。有关GDOP的计算可以从CRLB的推导公式中得到。通过对公式进一步分析可以得知，在时差、频差梯度较大以及时差曲线与频差曲线较大的区域定位精度较高。图7给出了定位误差达到1 000 km以上条件下，目标辐射源所处的地理位置，这些区域我们称之为定位盲区。

图6 不同定位精度的辐射源位置分布图Fig.6 GDOP of an area on the earth′s surface

图7 定位盲区仿真示意图Fig.7 Blind area for location system

图8 给出了载波频率在某频率为中心、10 GHz范围内变化时，定位精度的变化情况。

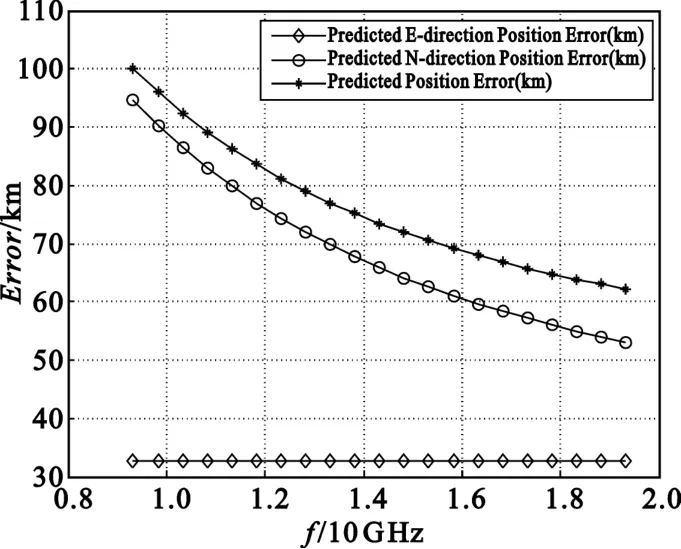
图8 载波频率对定位精度的影响Fig.8 Relationship between frequency and location accuracy

由于频差与载波频率息息相关，频差的梯度随着载波频率增大而增大，同时根据图4分析的结果得知，频差精度对南北方向的影响较大，因此可以得出随着载波频率的增大定位精度将提高，尤其是南北方向的定位精度较东西方向将明显提高，这与图8所反映的信息一致。

5 结论

本文在介绍双星定位原理的基础上，详细推导了在地球表面方程约束条件下的双星定位系统定位精度的CRLB公式。仿真结果表明，定位精度受定位参数估计精度、卫星星历、载波频率以及辐射源位置等因素影响，文中就各因素对定位精度的影响给出了物理解释。本文对定位精度的CRLB分析，可为定位系统指标设计与系统性能评估提供理论基础。同时，本文对定位盲时段与定位盲区域的展开分析，为定位系统选择最佳定位时间与最佳卫星组合提供了依据。

［1］Bardelli R，Haworth D P，Smith N G.Interference localization for the EUTELSAT satellite system［C］／／Proceedings of 1995 IEEE Global Telecommunications Conference.Singapore：IEEE，1995：13-l7.

［2］Haworth D P，Smith N G，Bardelli R，et al.Interference localization for EUTELSAT satellites-the first European transmitter location system［J］.International Journal of Satellite Communications，1997，15（3）：155-183.

［3］Ho K C，Chan Y T.Geolocation of a known altitude object from TDOA and FDOA measurements［J］.IEEE Transactions onAerospace and Electronic Systems，1997，33（3）：770-783.

［4］吴耀云，游屈波，哈章.双星系统对雷达无源定位的可行性分析［J］.电子信息对抗技术，2011，26（3）：1-5.

WU Yao-yun，YOU Qu-bo，HA Zhang.Analysis of Radar Emitter Positioning for Dual-Satellites Passive Location System［J］.Electronic Information Countermeasure，2011，26（3）：1-5.（in Chinese）

［5］龙宁，曹广平，王勤果.双星时差频差定位系统中的多信号定位技术［J］.电讯技术，2011，51（2）：16-20

LONG Ning，CAO Guang-ping，WANG Qin-guo.Multisignal Localization Technique for Dual-satellite Geolocation System Using TDOA and FDOA［J］.Telecommunication Engineering，2011，51（2）：16-20.（in Chinese）

［6］孙正波，叶尚福，瞿文中.利用互模糊函数实现卫星干扰源定位［J］.电波科学学报，2004，19（5）：525-529.

SUN Zheng-bo，YE Shang-fu，QU Wen-zhong.Satellite interference location using Cross Ambiguity Function［J］. Chinese Journal of Radio Science，2004，19（5）：525-529.（in Chinese）

［7］孙正波.同步卫星上行信号定位技术研究［D］.郑州：解放军信息工程大学，2006.

SUN Zheng-bo.Research on Dual-Satellite Geolocation system［D］.Zhengzhou：PLA Information Engineering University，2006.（in Chinese）

［8］瞿文中，叶尚福，孙正波.卫星干扰源精确定位的位置校正算法［J］.电波科学学报，2005，20（3）：342-346.

QU Wen-zhong，YE Shang-fu，SUN Zheng-bo.Algorithm of position calibrator for satellite interference location［J］.Chinese Journal of Radio Science，2005，20（3）：342 -346.（in Chinese）

［9］Kay S M.Fundamentals of Statistical Signal Processing：Estimation Theory［M］.Englewood Cliffs，NJ：Prentice-Hall，1993.

YAN Hang was born in Yancheng，Jiangsu Province，in 1980. He received the M.S.degree from Southwest Electronics and Telecommunication Technology Research Institute in 2006.He is now an engineer and currently working toward the Ph.D.degree. His research concerns signal processing and passive location.

Email：yanhang-57＠sina.com

姚山峰（1986—），男，四川安岳人，2011年于西南电子电信技术研究所获硕士学位，主要研究方向为信号检测、无源定位。

YAO Shan-feng was born in Anyue，Sichuan Province，in 1986.He received the M.S.degree from Southwest Electronics and Telecommunication Technology Research Institute in 2011.His research concerns signal detection and passive location.

Email：yao2004jessica＠163.com

勘误

本刊2012年第4期第568页“Fig.2 Diagram of partitioning data parellet”应为“Fig.2 Diagram of partitioning parallel data”，第477页作者英文简介末尾应添加“.”，第479页左栏第3行中上标［115］、第481页表1下第一行中上标［13］应去掉，特此更正。

本刊编辑部

Cramer-Rao Lower Bounds for Position Estimation in Dual-satellite Geolocation System

YAN Hang，YAO Shan-feng
（National Defense Key Lab on Blind Signal Processing，Chengdu 610041，China）

The principle of transmitter location using TDOA（Time Difference of Arrival）and FDOA（Frequency Difference of Arrival）of two satellites is introduced in this paper.Then，the Cramer-Rao Lower Bound

（CRLB）for the location accuracy is studied.In the CRLB，the factors such as the estimation accuracy of positioning parameters，the ephemeris，the position of transmitter and the carrier frequency are analysed.The physical explanations are also given.Simulations show the consistance between location accuracy change trend and CRLB and also confirm the correctness of theoretical analysis.

dual-satellite geolocation；TDOA／FDOA；parameter measurement error；location error；Cramer-Rao lower bounds

Pre-research Project during the 12th Five-year Plan（No.40901050301，513210901）；The National Defense Science and Technology Pre-research Project（9140A22020212JB5101）

TN971

A

10.3969／j.issn.1001-893x.2012.05.006

严航（1980—），男，江苏盐城人，2006年于西南电子电信技术研究所获硕士学位，现为工程师、博士研究生，主要研究方向为统计信号处理与目标无源定位；

1001-893X（2012）05-0634-06

2012-02-28；

2012-03-15

“十二五”预研项目（40901050301，513210901）；国防科技预研基金项目（9140A22020212JB5101）