蓝宝石抛光去除率试验的正交设计方法

孙振杰，费玖海，刘 涛

(中国电子科技集团公司第四十五研究所,北京065201)

在蓝宝石抛光过程中，影响抛光效果的因子有很多，比如压力、转速、抛光时间、抛光液的类型以及抛光垫的型号等，而且每个因子的水平数也很多，此时如果对这些因子的每个水平可能构成的所有组合条件均逐一进行试验，即进行全因子试验，试验次数就相当多。例如考察4个因子，每个因子有3个水平，则进行全面试验共需进行34=81次试验；又例如，考察7个因子，每个因子有2个水平，则进行全面试验共需进行27=128次，可见全因子试验次数多，所需费用高，所耗时间长，在实际工作中往往是办不到的。那么怎样做到尽量减小试验规模，同时保证试验误差较小，保证试验结果的可靠性呢？正交试验设计方法可解决这个难题。

1 正交试验

正交试验设计是一种通过部分试验并分析试验结果了解全面试验情况的一种试验方法。正交试验设计具有试验次数少，所安排的试验点具有代表性以及得到的试验结论可靠合理等优点。20世纪40年代，正交试验设计法首先应用于农业中，20世纪50年代推广到工业领域，取得了显著的效果。我国从20世纪60年代开始应用这一方法，20世纪70年代得到推广。

运用正交试验法，很重要的一步在于明确试验目的，并根据这个目的选定试验中需要考察的因子及其水平。基于正交试验法研究影响蓝宝石抛光去除率因子的目的主要是：明确蓝宝石抛光工艺中哪些抛光参数（或抛光条件）对蓝宝石抛光去除率影响显著，并寻找最佳工艺流程和工艺参数，最终使抛光去除率达到3～5 μm/h。

2 试验设计

2.1 试验方案

前面讲到进行全因子试验存在诸多弊端，因此在工程实践中通常采用加入中心点之后的二水平试验设计。由于影响蓝宝石抛光去除率的因子较多，通常先采用部分实施因子试验。其试验的目的主要是筛选因子，根据之前的工艺调研和经验，可能影响蓝宝石抛光去除率的因子比较多，主要包括：压力、转速、时间、抛光液类型、抛光液浓度、抛光液流量及抛光垫型号等，本试验要从以上众多因子中筛选出影响抛光去除率的显著因子。为减小试验规模，筛选因子的试验因子水平一般都取2，并同时加入若干次中心点重复试验，在相当程度上可以取代三水平的试验。我们根据以往蓝宝石抛光试验的经验，确定了试验各个因素的水平值，如表1所示。

表1 试验因子和水平

2.2 试验分析

在整个试验的分析过程中，按照试验设计分析五步法，并通过计算机Minitab软件进行分析，得出关于去除率数据方差分析结果如表3所示。

从ANOVA表中可以清楚地看出：

1)主效应项中，p-value为0.013，表示选定的模型总的效果是显著有效的；

2)在弯曲一栏中，p-value为0.065，表示响应变量（去除率）没有明显的弯曲趋势；

3)从各项主效应项的显著性来看，因子压力、转速、时间和抛光垫型号对应的p-value都小于显著性水平0.05，因此可以判定，这四项是显著的，而其余各项皆不显著。另外，从因子效应的Pareto图（如图1）可以更直观的看出各因素对去除率的影响主次依次排列为：抛光垫型号＞压力＞时间＞转速＞抛光液流量＞抛光液型号＞抛光液浓度；而压力、转速、时间、抛光垫型号为显著因子（大于 4.30）。

通过部分因子试验筛选出了影响抛光去除率的显著因子：抛光垫型号、压力、时间和转速；接下来为了寻找显著因子之间的最佳组合方式，我们将对之前筛选出的显著因子寻找最佳参数组合，以达到最优的抛光效果。

按照试验设计五步法流程，重新修改拟合模型中的“选项”，即删除不显著项后对新的改进模型重新进行分析。再次利用Minitab软件对去除率数据进行方差分析结果如表4所示。对于删减后的模型是否比原来有所改进，我们把两个模型计算的多元全相关系数R-Sq和修正的多元全相关系数R-Sq（调整）以及标准差的估计量s汇总成表（见表 5）。

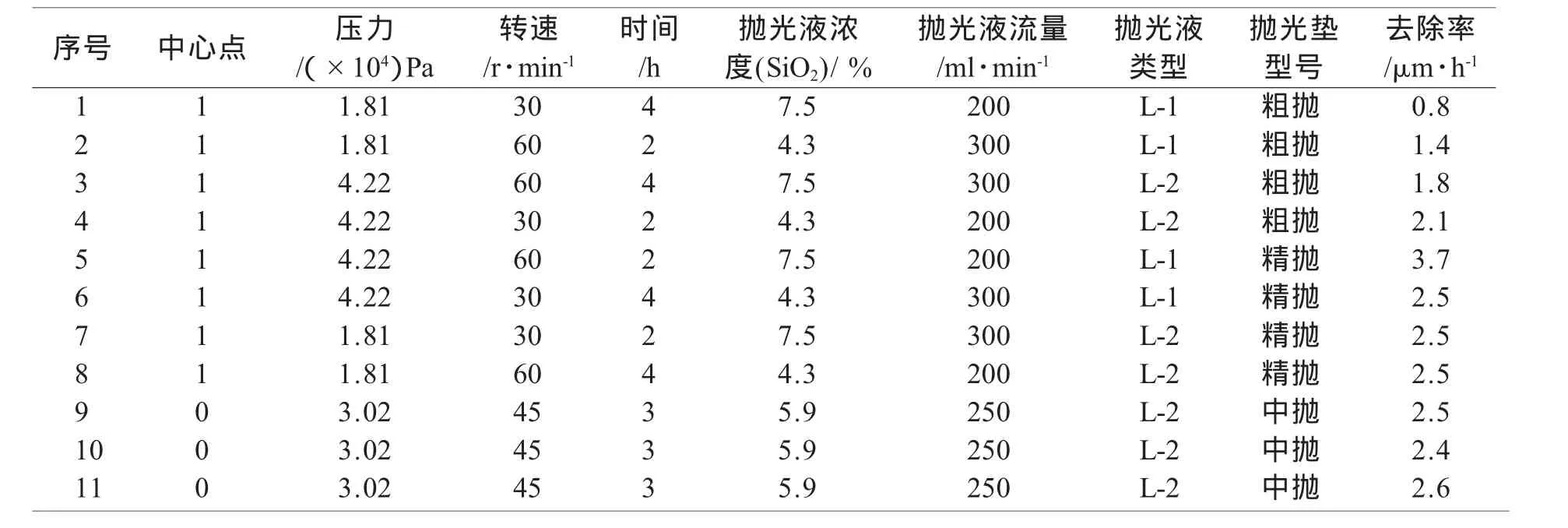
表2 试验正交表排列

表3 ANOVA（方差分析）表

图1 标准化效应的Pareto图

可以看出，由于模型项数减小了三项，R-Sq通常都会降低，但关键是看修正的R-Sq（调整）是否有所提高。本试验中，R-Sq（调整）由94.20%提高到98.10%，且删减模型后R-Sq与R-Sq（调整）之差减小；S值由0.24降为0.18，可见删除不显著因子之后，模型变好，回归的效果也更好。

新模型中各项数据没有明显异常，可以认为新模型是合理的模型。根据计算结果提供的数值，可以写出最后确定的回归方程：Rem＝1.481＋0.036P＋0.013W－0.263T－0.638Pad其中：Rem为去除率；P为压力；W为转速；T为时间；Pad为抛光垫；（精抛抛光垫 Pad＝1，粗抛抛光垫 Pad＝-1）。

表4 删除不显著项后的ANOVA（方差分析）表

表5 全模型与删减模型效果比较表

通过Minitab软件生成因子的主效应图，如图2所示，从图中可以看出：压力、转速、时间和抛光垫型号对于去除率的影响很显著；而且从图中还可以看出去除率随各因素变化的趋势，在试验参数范围内，压力、转速越大，去除率越大；时间越大，去除率越小；对于抛光垫类型的影响，精抛抛光垫的去除率更高，粗抛抛光垫的去除率偏低；而抛光液流量、浓度及类型对去除率影响不显著。

图2 去除率主效应图

通过Minitab优化器可求出试验区域内自动搜寻最优解，结果如下图3所示。

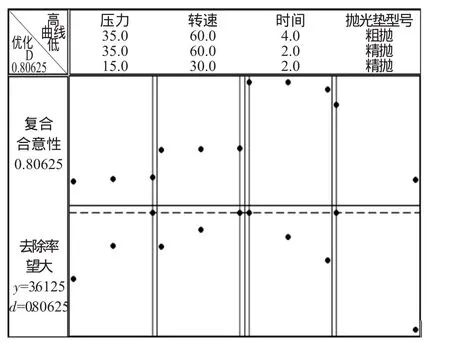
图3 响应变量优化器输出结果图

由图3可知，因子最优组合如表6所示。

表6 因子最佳参数组合

本试验预计的最优结果是 3.6 μm/h，而3～5 μm/h的去除率就可以满足基本的工艺使用要求，与实际目标很接近，达到目标要求。为了确保按最佳条件进行抛光时能获得预期效果，在最佳点处经过多次现场抛光试验，结果表明试验得到最佳参数组合进行抛光，实际抛光去除率与分析得到的预测值（3.6 μm）比较接近，说明以上分析与预测是准确可靠的。

3 试验总结

影响蓝宝石抛光去除率的因素还有很多，例如：室温、抛光过程中抛光盘温度等。该试验中，根据经验将这些因素设定为经验值再进行分析。通过以上分析可以认为，对去除率影响显著的主要因素有：压力、转速、时间、抛光垫；而抛光液浓度、流量及类型对去除率影响不显著，可能是因为本试验设置的浓度及流量值，相对抛光过程的化学反应速度而言，已经达到饱和，因此提高浓度及流量已经对去除率影响不明显。

人们常说“设备研制开始于工艺，用之于工艺”。利用正交试验的方法科学的设计工艺试验的方案，可以用最小的试验次数和试验成本研究设备使用的各项工艺参数对产品质量或生产效率的影响，并得到合理近似的数学模型，有利于我们科学的评估设备性能的优劣，正确判断设备是否能够达到实际工艺线的要求。从这个意义上来讲，正交试验设计对设备研制也具有积极的意义。

[1]马林，何桢主编.六西格玛管理（第二版）[M].北京：中国人民大学出版社.2007:296-355.

[2]《健壮设计手册》编委会编著.健壮设计手册[M].北京：国防工业出版社.2002:185-191.

[3][美]D.C.蒙哥马利著，汪仁官等译.实验设计与分析（第三版）[M].北京：中国统计出版社，1998:298-340.

[4]何少华，文竹青，娄涛.试验设计与数据处理[M].长沙：国防科技大学出版社.2002:62-65.