河道单宽测流法探讨

□张少伟 □王国建（安阳水文水资源勘测局）

水文测验规范规定：“精简分析是流量测验工作中的一个重要环节，它的目的是在保证流量测验成果精度的前提下减少测流工作量，缩短测流历时，提高测报质量。”规范还规定了一般江河水文站的精简分析有3个项目，即常测法、简测法、间测法。在实际精简分析工作中一般是进行一种固定垂线单宽测流法分析，这种方法是在建立垂线单宽流量和断面平均单宽流量关系的基础上，精简流速仪测流方法，达到规范规定的精简目的。

1.基本原理

江河测站水文测验断面在比较稳定的测站控制条件下，水位流量关系和断面水流结构都存在着一定形式，各部分水体之间的流速、流量等各项参数因素也存在一定的相互关系。这些水文参数随水位变化也按一定的规律变化。当测验河段或测验断面的控制条件和水利特性不发生明显改变时，它们之间的关系和随水位变化的规律也不会发生明显的改变。具备了这些条件，如规范指出“有利简化测验工作，保证资料质量”，而单宽测流法的基本出发点也在这里。

所谓单宽流量,即垂线平均流速与垂线水深的乘积

q—垂线单宽流量（m3/s）；vm—垂线平均流速（m/s）；h—垂线水深（m）。

而断面总流量Q是全断面单宽流量q沿河宽的积分：

Q=∫0B q.dB;B—水面宽。

单宽流量在断面上的分布形式，取决于断面形状和流速分布。规范是假定水深和流速在断面上连续函数分布而采取有限差的形式进行计算流量的。现在我们同样假定单宽流量在断面上呈现连续函数分布。这里，我们以单宽流量在断面上呈现抛物线分布进行研究。

为了分析方便，我们将水面宽取相对值

令：m=b/B

m—相对水面宽；b—从岸边算起的部分水面宽；B—全水面宽。

同时，我们按照水文习惯，将坐标原点设于一岸水边，如图1。

则此抛物线等于将标准抛物线方程（x2=-2py，此处x=m，y=q）的坐标原点平移至（m=-0.5，q=-q0.5）处。故图1抛物线方程为

P—抛物线的参数；

q0.5—相对河宽0.5处的单宽流量，也是最大单宽流量。

已知抛物线通过原点（0，0）或另一水边（1,0），将此已知条件代入（1）式。即可求得P值：

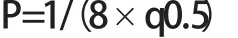
将P值代入（1）式，化简得：

（m-0.5）2=-2×1/（8×q0.5）（q-q0.5）

（2）式即为单宽流量呈现、抛物线分布时的函数式。

设此抛物线与m坐标轴间的面积为F,则知道F等于相对水面宽从0到1的积分；同时也是相对水面宽下的流量，即为断面平均单宽流量q平均

（3）式表明了当单宽流量在断面上呈现抛物线分布时断面平均单宽流量和最大单宽流量的关系，将（2）和（3）合并化简得：

（4）式即为断面平均单宽流量和任意位置单宽流量及其相对河宽的关系。

如果选定固定相对河宽的单宽流量进行分析（此时实际垂线位置将是变动的），则（4）式中1/6（m-m2）将是一个固定常数令 k=1/6（m-m2），则 q平均 =kq（5）是直线式。

如果选择固定垂线位置的单宽流量进行分析，垂线单宽流量q与水位G有着函数关系，即：

实际工作中在比较稳定的断面形状下，河宽B和固定垂线至水边的部分宽b都是水位的函数，因此相对河宽m也是水位G的函数，即：

将上式代入（4）得

q平均=q/{Φ[f（q）]-Φ[f（q）2]

是复合函数式。

但是由于天然河道的多变性和复杂性，就是在单式河槽断面其形状呈U形时，单宽流量在断面上的分布也不一定呈标准抛物线型，或其它标准线型。因而，当为复式河槽时，单宽流量分布曲线甚至会出现两个以上的峰值。这样，在实际情况下要找出其分布函数式比较困难的。但并不是说垂线单宽流量和断面平均单宽流量之间不存在相关关系。而是说明天然河道的上述关系比较复杂。有的站，可能以固定相对河宽建立关系较好，另一些站，可能以固定实测垂线位置建立关系比较好。所以，在工作中必须通过实测资料分析，找出最佳方案。

2.对单宽测流方法的估价

2.1 单宽流量测验方法是简化测流的一种方法，目前，尚在试探分析实践检验中，有些方面还需要在不同河道站进行实测资料论证。但从单宽测流法与简测法对比看，有不必施测或借用水边断面的优点。在保证资料精度的条件下，工作更加简化。

2.2 单宽流量测验方法适用于河道控制良好断面稳定的测站。但对于虽有冲淤变化剧烈控制条件较差的测站能否适用，尚需研究。