基于连续能量蒙特卡罗方法的均匀化群常数计算

李满仓，王 侃，姚 栋

（1.清华大学工程物理系，北京100084；2.中国核动力研究设计院核反应堆系统设计技术重点实验室，四川 成都610041）

在反应堆物理计算中应用的确定论方法和蒙特卡罗方法方法各有优缺点：确定论方法一般计算速度较快，蒙特卡罗方法通常精度上具有优势。传统的反应堆物理分析以确定论为主，蒙特卡罗方法通常只是作为补充手段。随着计算机技术和高性能算法的不断发展，完成物理计算所需时间越来越短，人们希望在更高的平台上追求速度与精度的平衡；另一方面，新型复杂堆芯概念的提出，对程序所能模拟的几何和物理复杂度也形成挑战。这种背景下，联合蒙特卡罗方法和确定论方法优势的研究是近几年的一个热点方向[1－3］。其中一个思路是应用蒙特卡罗方法计算组件为确定论堆芯程序提供均匀化群常数。这种方案沿用传统的“两步法”，提高对复杂几何和物理的适应性，避免复杂的共振计算，同时保证堆芯计算在可接受的时间内完成。使用同一个蒙特卡罗组件均匀化程序和同一套数据即可模拟计算任意几何构型的组件和任意能谱的堆芯，普适性很好。

近几年国际上一直在探索应用蒙特卡罗方法进行组件均匀化[4－11］，应用涉及沸水堆、高通量堆、乏燃料组件和球床堆等。原则上所有的蒙特卡罗程序都可以通过计数能量和体积区间的反应率和通量获得均匀化截面。但是广泛使用的蒙特卡罗程序如 MCNP[12］、KENO[13］、TRIPOLI[14］、MVP[15］等不具备这样的功能。应用连续能量蒙特卡罗方法进行组件尺度的均匀化计算主要涉及两个大的问题：一是群常数的基本产生方法，蒙特卡罗方法相对于确定论有一定的特殊性，针对确定论发展的均匀化理论并不能直接应用在蒙特卡罗方法中；二是群常数等效均匀化，均匀化过程必须做等效处理，蒙特卡罗方法均匀化也不例外。本文研究和探索解决第一个问题，即蒙特卡罗方法计算产生组件均匀化群常数，特别是散射矩阵和高阶勒让德系数。扩散系数在蒙特卡罗方法中没有对应的物理量，通过研究采用P1截面计算。对于全反射单组件计算模型，本文应用BN理论对均匀化群常数进行泄漏修正。

以下首先介绍本文蒙特卡罗均匀化群常数的计算方法，之后在组件和堆芯两个层次对方法进行验证。

1 计算方法

1.1 一般群常数计算方法

本文一般群截面和群常数包括总截面、吸收截面、中子产生截面、裂变截面和中子裂变谱等，基本计算思路是使用径迹长度方法估计反应率和通量，通过二者之商得到截面。

定义时间积分体积权重的群通量φg，

本文的所有计算都是静态的，和时间无关。式（1）以及下面公式中的时间变量t，指的是粒子从产生到消失的时间。其中通量

改写成距离的形式

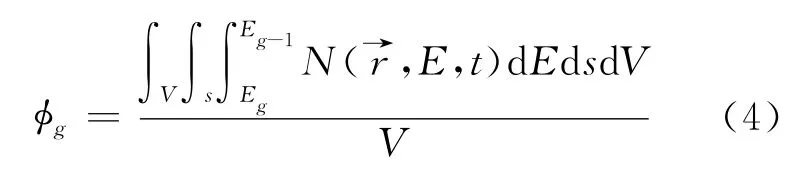
其中s是粒子从产生到消失的距离。在蒙特卡罗方法中，粒子密度等价于每单位体积的粒子权重W的总和，而距离等价于径迹长度TL。因此（3）式可以写成

其中，WTLiV（E）为第i个粒子在能量E体积V处的粒子权重和径迹长度的乘积；Wi0是第i个粒子的初始权重；N为跟踪的粒子总数。

类似的，对于反应率，有下式成立：

根据（5）式和（6）式即可得到均匀化群截面

1.2 散射事件方法

群常数中的群间转移截面和散射截面的高阶勒让德分量不能直接应用确定论的方法获得。在连续能量点截面数据库中没有相应的微分散射截面，散射反应是通过总散射截面和散射角分布等量体现的；非弹性散射中的出射中子能量也有一定的分布。为此，论文提出散射事件方法计算散射矩阵和勒让德分量。散射事件方法利用蒙特卡罗直接模拟的特点，跟踪模拟散射事件，当散射发生时，统计能量和角度的变化，在此基础上获得散射矩阵和勒让德系数。

对于散射矩阵，分别记录散射事件前后的中子能量，判断此能量所属的分群能量区间并进行统计，获得散射份额

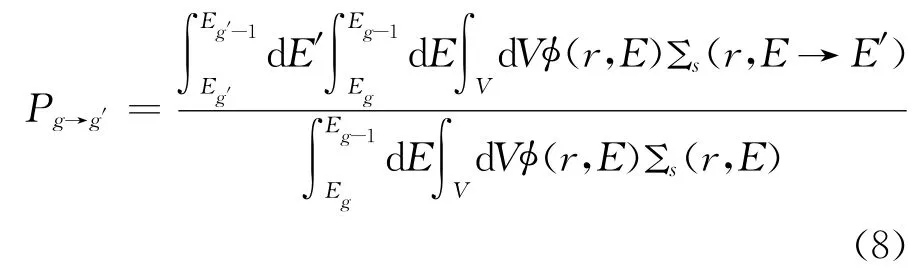
群间转移截面通过散射份额与散射截面的乘积获得：

应用蒙特卡罗方法产生组件均匀化群常数时同时考虑下游堆芯应用扩散方法和输运方法计算，因此有必要产生高阶勒让德分量，或称Pn截面。

以一维问题为例，勒让德分量的定义如下：

Σs，n和φn是使用勒让德多项式展开散射截面和中子通量的系数，可以利用勒让德多项式的正交性求得。其中Σs，0是群间转移截面，φ0是中子注量率。n≥1时，应用蒙特卡罗方法统计权重函数φn（z，E）时，由于蒙特卡罗方法的涨落特性，会造成很大误差。假设φn与φ0成比例关系，即

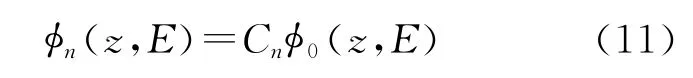
应用微分散射截面的定义

（10）式可以写成

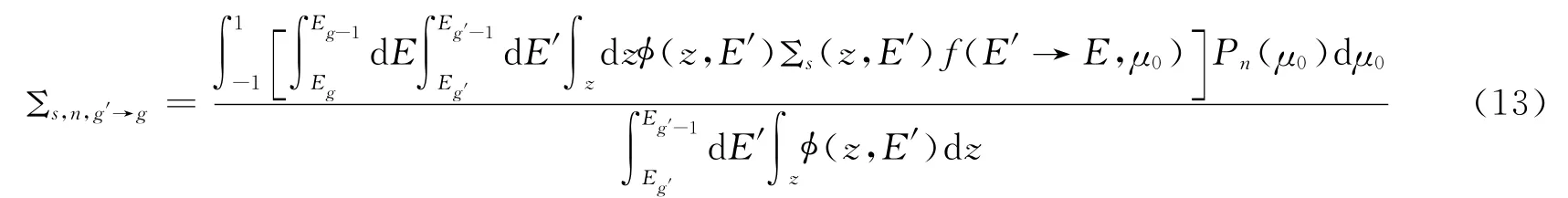
（13）式就是本文Pn的计算方法：首先在－1到1之间分割一定数目的角度区间，根据散射事件前后角度的改变获得散射角余弦，在相应的角度区间上增加计数；粒子跟踪完毕，可以获得各个角度区间的份额，然后利用勒让德关系式的定义，计算数值积分。

1.3 扩散系数

扩散系数是输运方程到扩散方程近似时引入的参数。扩散系数定义为：

其中Σtr，g为输运截面。确定论方法使用多群核数据库中包含有各核素的输运截面，而在连续能量蒙特卡罗数据库中没有对应的量。作为初步实现蒙特卡罗方法组件均匀化的方法，本文输运截面通过下式获得：

其中 Σt，g为总截面，Σs，1，g→g是P1系数的自散射截面，应用1.2节所述计算方法获得。

1.4 泄漏修正

组件均匀化计算一般采用全反射单组件局部均匀化模型，这种模型没有考虑组件在堆芯中的真实状态：组件的边界存在中子净流，组件通常处于临界状态。蒙特卡罗方法均匀化也要还原两步法计算流程中组件在堆芯的临界状态，本文采用确定论方法中成熟的BN理论修正泄漏效应，基本思路是：使用B1方程中的曲率B2表征堆芯的有限性，使用近似渐近能谱考虑中子泄漏。

多群形式的B1方程

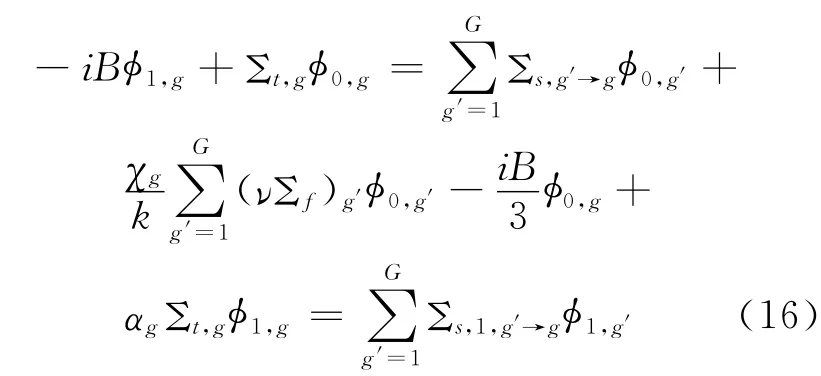
其中

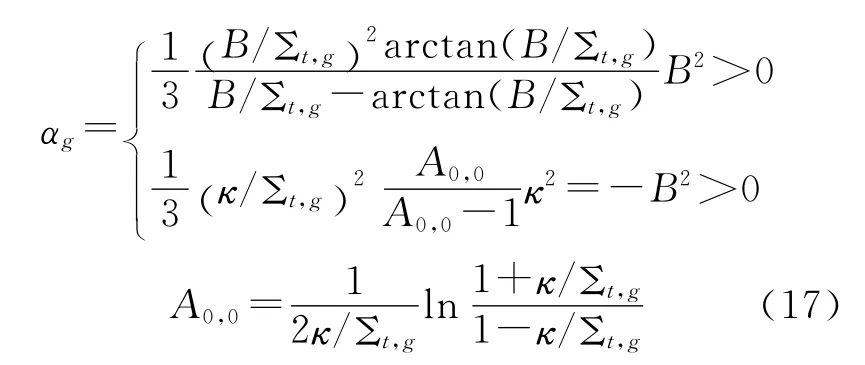
（16）式和（17）式中B2为临界曲率，其他参量与一般多群扩散方程中的意义相同。通过求解（16）式获得临界渐近能谱φLn，使用临界渐进谱修正无限介质谱，得到临界谱φCn，i：

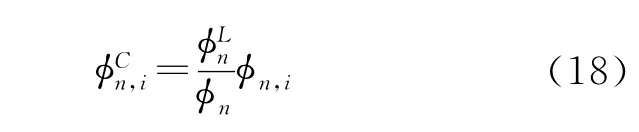
临界谱是考虑了临界效应的能谱，应用该能谱作为群常数归并时的权重函数：

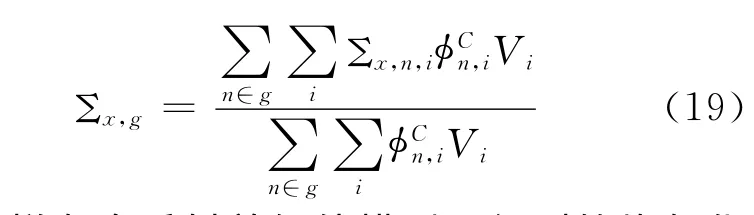
这样在全反射单组件模型下得到的均匀化群常数就可以归并出考虑了临界效应的少群常数。该少群常数用于堆芯计算即可提高其精度。

2 数值验证

2.1 验证方法

数值验证部分蒙特卡罗方法均匀化群常数采用MCMC程序计算。MCMC程序是本文作者编制的基于连续能量蒙特卡罗方法组件均匀化程序。为展示本文研究的方法和蒙特卡罗均匀化的特性，以下计算中MCMC群常数没有应用等效均匀化。MCMC计算获得的均匀化群常数将与CASMO－3[16］进行对比。应用多群蒙特卡罗程序MCMG[17］和细网有限差分程序CITATION[18］计算堆芯，获得keff和通量分布，与参考解MCNP[19］的计算结果对比，验证方法的可靠性。

MCMC具有产生任意数目群参数的能力。表1给出了2群、4群和7群的能群边界，本文将考察3种能群结构数对物理计算结果的影响。

表1 2群、4群和7群的能群结构Table1 Group boundaries for the 2－，4－and 7－group structures

组件计算时如果应用全反射边界条件，净流为零，中子输运方程和扩散方程中的泄漏项为零。以多群扩散方程为例：）

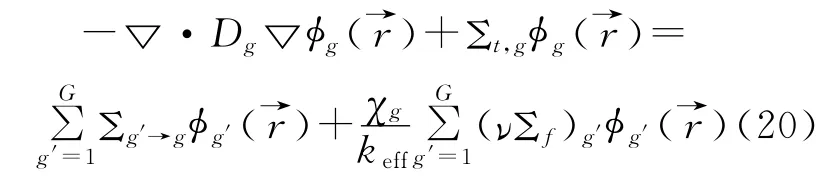
对于全反射边界条件，方程（20）写作

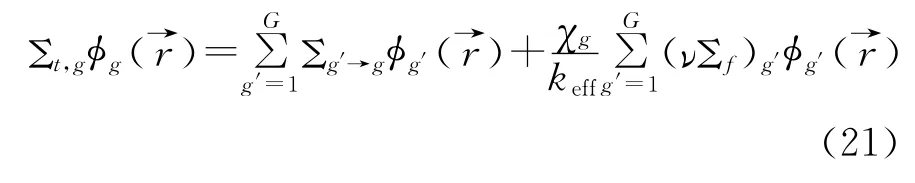
即

根据（22）式可以根据均匀化群常数计算kinf的理论值。这可以作为另一个验证组件群常数有效性的手段。

2.2 AFA3G组件验证

图1所示为17×17形式的AFA3G组件，富集度为2%。分别使用CASMO－3和MCMC计算产生控制棒全提（ARO）和控制棒全插（ARI）两种工况的均匀化群常数。

图1 AFA3G组件模型Fig.1 AFA3Gassembly model

表2比较了MCMC与CASMO计算的2群群常数。从表中可以看到：无论是ARO工况还是ARI工况，除了跳群散射截面，MCMC与CASMO－3计算的群常数相对偏差都在5%以内，对于截面而言，这是很小的；不同群的群间转移截面差别较大，考虑到热群到快群向上散射截面本身数值就很小，在很多2群堆芯计算中甚至设为0，其影响并不显著。

表2 AFA3G组件CASMO－3和MCMC计算的2群群常数比较Table2 Comparison between two groups of constants in MCMC and CASMO－3calculations for AFA3Gassembly

表3给出了CASMO－3和MCMC计算的群常数解析解kinf与参考值的比较。采用MCMC群常数计算的解析解kinf与参考值符合较好，随着能群数目的增加，结果越来越好；总体来说，CASMO群常数的结果要差一些，而且没有特征值随能群数目增加而改善的趋势。这是因为确定论组件计算时采用多群数据库，MCMC计算应用连续能量，均匀化归并少群参数时保留了更多连续能量的信息。

表3 AFA3G组件kinf解析解与参考值比较Table3 Theoretical solutions ofkinffor AFA3Gassembly

2.3 组件层次几何适应性研究

图2是套筒状燃料元件模型，燃料和包壳呈套筒状相间排列；图3为CANFLEX重水堆新型燃料棒束组件模型，含43根燃料棒；图4所示的双排六边形燃料组件是超临界水堆的候选组件。

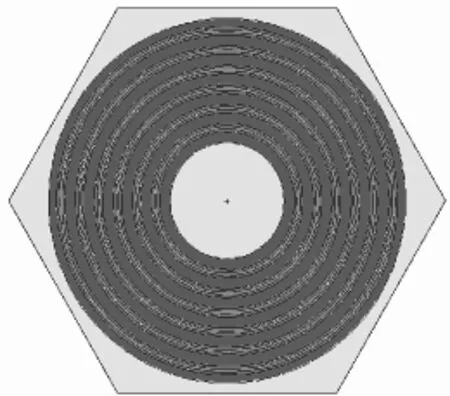
图2 套筒状燃料元件模型Fig.2 Cylindrical assembly model

图3 CANFLEX组件模型Fig.3 CANFLEX assembly model

图4 SCWR组件模型Fig.4 SCWR assembly model

3种组件MCMC少群常数的kinf解析解和参考解的比较在表4中给出。结果表明：对不同几何构型和材料组成的组件，MCMC群常数反算kinf与MCNP参考值符合均较好，随能群数目增加而更加吻合。这说明MCMC计算的组件群常数（总截面、吸收截面、中子产生截面、散射矩阵和裂变谱）是准确有效的。相比目前实际工作中每种燃料组件的计算都需要专门的组件程序而言，MCMC有良好的几何适应性。

表4 套筒状燃料元件、CANFLEX组件和SCWR组件理论kinfTable4 Theoretical solutions of kinf for cylindrical assembly，CANFLEX and SCWR assembly

2.4 简化压水堆堆芯验证

堆芯尺度验证在图5所示的简化压水堆模型上进行。使用17×17形式的AFA3G组件，富集度为1.2%和2.0%的组件分别有24个和21个，两种组件按棋盘布置。分别计算ARO和ARI两种工况，ARI工况时2.0%组件中插入Ag－In－Cd控制棒。反射层为20cm厚的轻水。利用MCMC产生的群常数进行多群蒙特卡罗MCMG和细网差分CITATION计算，比较堆芯keff和通量分布。反射层计算采用超组件模型。

图5 简化压水堆模型堆芯构成Fig.5 Simplified PWR core configuration

表5是堆芯keff的计算结果。表中MCMC群常数和CASMO群常数都是经过泄漏修正的，MCMC群常数没有应用任何形式的等效均匀化，CASMO群常数使用G因子方法调整相对吸收率守恒[20］。MCMG计算中比较加入了P1阶勒让德分量的效果。2、4和7表示使用的少群群常数分别是2群、4群和7群。可以看到，应用MCMC群常数的输运计算和扩散计算keff基本随能群数目增加与MCNP参考值的相对偏差变小。应用MCMC群常数的扩散计算精度优于确定论CASMO程序。加入P1高阶分量的MCMG计算堆芯keff比P0的计算结果好很多，因为P1截面的加入会改善角度信息。

表6是通量分布的偏差比较，包括最大偏差MAX、平均偏差AVG和均方根偏差RMS其中en为 MCMG或CITATION与MCNP参考值的相对误差）。从结果看，CITATION与参考值偏差较小，而MCMG在少能群数目时偏差较大，需要更高阶Pn截面完成堆芯输运计算。由于蒙特卡罗方法统计涨落的原因，MCNP参考值本身在堆芯对称位置的分布也有约1%的偏差，所以总体而言，通量分布符合的很好。

表5 简化压水堆堆芯keff比较Table5 keffcomparison for simplified PWR core

表6 简化压水堆堆芯归一化通量分布偏差比较Table6 Normalized flux distribution error comparison for simplified PWR core

3 结束语

本文旨在将蒙特卡罗方法对复杂几何和物理的适应性以及连续能量的优势应用于传统的两步法反应堆物理计算流程中，根据蒙特卡罗方法的特点总结和提出了蒙特卡罗方法产生组件均匀化群常数的方法。通过组件和堆芯两个尺度的数值验证，表明本文计算的蒙特卡罗组件群常数具有较好的性能，在几何上有很强的适应性，而且保留了更多连续能量信息。基于这些优势，蒙特卡罗方法均匀化和确定论组件堆芯计算的反应堆物理分析流程，是下一代堆芯设计计算中极有潜力的候选方法。

连续能量蒙特卡罗方法均匀化产生群常数后，也要应用等效均匀化理论保证均匀化前后的反应率和界面流守恒，以最大限度的保留精度，体现蒙特卡罗方法的适用性。另外，均匀化群常数随燃耗变化，为完成堆芯的燃耗计算，蒙特卡罗均匀化也要具备燃耗功能。这些是完善蒙特卡罗方法均匀化的研究方向。

[1]Brown F B，Martin W R，Mosteller R D.Monte Carlo－Advances and Challenges[C］／／Workshop at PHYSOR－2008，14－19September，Interlaken，Switzerland.Los Alamos National Laboratory，2008：159.

[2]Martin B.Advances in Monte Carlo Methods for Global Reactor Analysis [C］／／Joint International Topical Meeting on Mathematics ＆Computation and Supercomputing in Nuclear Applications（M＆C＋SNA 2007），April 15－19Monterey，California，USA.2007.

[3]Yesilyurt G，Martin W R，Lee J C.A Coupled Monte Carlo／Collision Probability Method for VHTR Analysis[J］.Transactions of the American Nuclear Society，2008，99：753－754.

[4]Ilas G，Rahnema F.A Monte Carlo Based Nodal Diffusion Model for Criticality Analysis of Spent Fuel Storage Lattices[J］.Annals of Nuclear Energy，2003，30（10）：1089－1108.

[5]Van der Marck S C，Kuijper J C，Oppe J.Homogenized Group Cross Section by Monte Carlo[C］／／PHYSOR－2006American Nuclear Society's Topical Meeting on Reactor Physics， Sept.10－14， Vancouver， BC，Canada.2006.

[6]Tohjoh M，Watanabe M，Yamamoto A.Application of Continuous－energy Monte Carlo Code as a Cross－section Generator of BWR Core Calculations[J］.Annals of Nuclear Energy，2005，32（8）：857－875.

[7]Redmond II E L.Multigroup Cross Section Generation Via Monte Carlo Methods[D］.Massachusetts Institute of Technology Dept.of Nuclear Engineering，1997.

[8]Rahnema F，Ilas G，Hudson N H，et al.On the Fewgroup Cross－section Generation Methodology for PBR Analysis[J］.Annals of Nuclear Energy，2006，33（11－12）：1058－1070.

[9]Blomquist R N.VIM Monte Carlo Neutron／Photon Transport Code[EB／OL］.[2010］.www.vim.anl.gov.

[10]Maiorov L V.MCU Code：MCU Project Home Page[EB／OL］.[2010］.www.mcu.vver.kiae.ru／eareal.

[11]Leppänen J.PSG2／Serpent－A Monte Carlo Reactor Physics Burnup Calculation Code[EB／OL］.[2010］.www.montecarlo.vtt.fi.

[12]Team X－M C.MCNP— A General Monte Carlo NParticle Transport Code， Version 5， Volume I：Overview and Theory[R］.LA－UR－03－1987，April 24，2003.

[13]Hollenbach D F，Petrie L M，Landers N F.KENOVI：A General Quadratic Version of the KENO Program[R］.ORNL／NUREG／CSD－2／V2／R6，Oak Ridge National Laboratory，1998.

[14]Diop C M，Petit O，Dumonteil E，et al.TRIPOLI－4：a 3DContinuous－Energy Monte Carlo Transport Code[C］／／PHYTRA1：First International Conference on Physics and Technology of Reactors and Applications，March 14－16，Marrakech，Morocco.2007.

[15]Matsuda S.MVP／GMVPⅡ：General Purpose Monte Carlo Codes for Neutron and Photon Transport Calculations based on Continuous Energy and Multigroup Methods[R］.JAERI 1348，Japan Atomic Energy Research Institute，2005.

[16]Studsvik.CASMO－3User's Manual[R］.Studsvik／SOA－94／9，Studsvik of America，1994.

[17]邓力 .三维多群P5中子输运蒙特卡罗程序 MCMG－I使用说明[R］.北京：北京应用物理与计算数学研究所，2011.

[18]张瑞茵，赵翊民.CITATION核反应堆堆芯分析程序[R］.清华大学核能与新能源研究院，1986.

[19]Team X－M C.MCNP—A General Monte Carlo NParticle Transport Code，Version 5，Volume Ⅱ：User's Guide[R］.LA－UR－03－1987，April 24，2003.

[20]Studsvik.CASMO－3Methodology [R］.Studsvik／NFA－88／49，Studsvik，1988.