海岸效应对近海地区大地电磁测深数据畸变作用研究

张 帆，魏文博，3＊，金 胜，叶高峰，景建恩，张乐天，董 浩，谢成良，王 辉

1 中国地质大学（北京）地球物理与信息技术学院，北京 100083

2 地下信息探测技术与仪器教育部重点实验室，北京 100083

3 地质过程与矿产资源国家重点实验室，北京 100083

1 引 言

中国作为一个海洋大国，海岸线长达18000km［1］.“深部探测技术与实验研究”专项的第一项目（大陆电磁参数标准网实验研究）下属“西南—华北阵列式区域大地电磁场标准网示范性实验研究（SinoProbe－01－02）”课题中的部分大地电磁测深点就分布在近海岸线地区.但是，在近海地区进行大地电磁测深工作，通常难以采集到高质量的大地电磁测深数据，这主要是受到海岸效应影响的结果［2］.由于大地电磁测深观测结果受海岸效应影响而发生畸变，很难直接利用近海地区大地电磁测深资料获取地下深部较为可靠的电性结构信息；因此，必需研究海岸效应对近海地区大地电磁测深数据的畸变规律，为寻求有效的校正方法奠定基础.

Parkinson［3］最初在澳大利亚的近海地区观测到了地磁场的大幅度波动现象，并指出了这种波动现象可能是海洋电磁感应的结果［4］.Jones等［5］通过建立地电模型，分析了海洋对陆地测点的电磁感应现象.随后Parkinson和Jones［6］对海岸效应做了综合性的解释，认为海岸效应可通过某一频率的磁场垂向分量与水平分量的比值，以及感应矢量参数来描述.随着大地电磁测深方法在近海地区的研究工作逐渐增多，人们开始尝试利用海岸效应的影响进行大地电磁测深数据校正.Nolasco等［7］首先利用电磁畸变张量对近海地区采集的大地电磁测深数据进行了一维模型海岸效应校正.杨文采等［8］通过正演模拟的方法分析了一维地电模型下海岸效应对大地电磁测深数据的影响，为反演方法的选取提供依据.近年来，二维和三维地电模型的海岸效应研究逐步引起人们的重视，地下介质精细的电性结构信息也成为了海岸效应校正必不可少的先验信息［9-10］.由于海岸效应的复杂影响，仍需进一步分析研究海岸效应对近海地区大地电磁测深数据的畸变作用.

本文通过正演模拟的方法，分析和总结海水深度变化和海底地形变化对近海地区大地电磁测深数据的畸变影响；利用一维Occam反演算法和二维非线性共轭梯度（NLCG）反演算法，对三维正演模型的大地电磁测深响应数据进行一维反演和二维反演计算，分析近海地区大地电磁测深反演结果的可信程度；以近渤海地区B1测点的实测大地电磁测深资料为例，评估近渤海地区所采集的大地电磁测深资料的数据质量.

2 海岸效应

实测的大地电磁测深响应主要受测区人文干扰、环境噪声、近地表的电性不均匀体以及复杂的地形条件的影响而发生畸变.Robust数据处理技术的应用可以有效地减小测区环境噪声对大地电磁测深资料的影响程度［11］.由近地表的电性不均匀体所引起的电磁场畸变可以利用阻抗张量分解技术来压制［12］.大量的地形校正方法也成功地应用到了陆地和海洋大地电磁测深研究中［13-15］.但是，测区范围内高电导率的海水的存在也会严重影响到大地电磁测深资料，这主要是由于海洋和陆地之间巨大的电阻率差异造成的.低频大地电磁场趋肤深度通常可以达到数百公里，当测点与海岸线的距离小于目标频率的大地电磁场趋肤深度时，海洋的存在将会影响海岸附近电磁场的分布，使得近海地区大地电磁测深响应曲线受畸变［10，16］，这即是通常所指的“海岸效应”.

地表某一测点处的变化磁场是时间和空间位置的复杂函数.一般而言，在电离层和磁层中存在有运动电荷，由该运动电荷引起的变化电磁场称为一次场.当一次场向地面传播靠近水平地面时，可以近似为水平入射的平面波场.由于地球具有非零的电导率值，变化的一次场在地球内部传播将因为电磁感应而产生涡旋电流，从而产生相应的变化磁场，这种由感应涡旋电流产生的变化磁场称为二次场.由于地球内部的电性结构具有复杂的空间分布，因此，二次场亦是空间变量的复杂函数.实际上，地表某一测点处的变化磁场即是一次场和二次场的叠加场，因而具有复杂的时间和空间分布特征.

通常，在距离海岸线较远的内陆地区，变化磁场的垂向分量要远小于其水平分量，即变化磁场ΔB的方向趋近于水平方向.当测点位于海岸线附近时，变化磁场的垂向分量急剧增大，其方向不再趋于水平方向，而是向海洋方向倾斜，这即造成了海岸效应［6，17］.

对于平面电磁波场而言，磁场的垂向分量和水平分量之间具有相关性［18］，相应的表达式为：

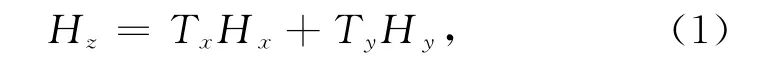
式中，Tx和Ty是磁场倾子在水平方向上的两个正交分量，磁场倾子T的大小可以用来度量由地下介质电阻率水平梯度引起的磁场垂直分量，其方向指示了地球二维构造的法线方向.Hx，Hy，Hz是磁场在笛卡尔坐标系下的三个正交分量.其中，Hx和Hy是磁场的两个水平分量，Hz是磁场的垂向分量.

感应矢量是分析海岸效应直接且重要的工具［19］.感应矢量定义为磁场垂向分量与其水平分量的比值.由于横向电导率梯度的变化产生了垂向磁场，因此可以利用感应矢量来判断导体内是否存在横向电导率异常.根据Parkinson准则，感应矢量的方向为介质中电性异常体内电流汇聚的方向［6］.

高导海洋对电磁场的吸收作用非常强烈，对海岸附近电磁场的分布具有较大的影响.对于一维层状介质模型来说，海岸线附近纵向电场减小，横向电场增大，且磁场垂向分量急剧增大.视电阻率和相位随频率的变化曲线出现严重畸变，尤其在低频部分这种畸变更为明显.因此，在近海地区开展大地电磁测深工作时，必须考虑海岸效应的影响，否则有可能给地质解释带来较大影响，甚至可能得出错误的结论［8］.

3 大地电磁测深正、反演方法

对三维地电构造的大地电磁测深响应特征进行理论研究通常采用正演模拟的方法.自20世纪70年代中期开始，三维大地电磁正演模拟技术取得了长足的进展.其中，以Mackie等［20］发展的交错网格有限差分三维电磁模拟算法最具代表性.随着计算机技术的进步，三维大地电磁正演模拟研究已趋于成熟，有限差分法以计算简单、快速，适于模拟复杂的地质体等特点，成为了三维大地电磁正演模拟计算的主要方法［21］.

随着大地电磁三维正演计算技术的发展，大地电磁三维反演研究日趋升温；但目前仍处于研究阶段，其算法技术不够成熟，在实际应用中的有效性也有待进一步验证.目前，大地电磁测深资料处理解释的主要手段仍是技术相对成熟的大地电磁测深一维和二维反演［22］.

一维Occam反演方法以其稳定收敛、受初始模型影响小的特性在大地电磁测深一维反演问题中得到了广泛的应用，是一种有效的数据处理解释方法.Constable等［23］在1987年提出了Occam反演方法，认为在反演中为了获得最优解，反演模型应尽可能的简单、光滑，为了压制来自非数据的构造，模型的粗糙度应尽可能的小.但是由于其需要直接计算雅可比矩阵，在解决高维和大型问题时反演速度较慢.二维非线性共轭梯度（NLCG）反演方法［24］利用线性系统的叠加原理和格林函数的性质，策略性地实现了雅可比矩阵与一个向量乘积的整体计算，从而极大的提高了反演速度，在野外观测数据大量增加的大地电磁测深方法中发挥了重要的作用，成为国际上广泛应用的二维反演方法.但是NLCG反演方法对初始模型的依赖性较大，反演效果的优劣与给定的初始模型好坏关系密切.Occam反演方法和NLCG反演方法具有很好的互补性，可以利用一维Occam反演计算出拟二维地电剖面，以该地电剖面为初始模型进行二维非线性共轭梯度反演，以达到更好的反演效果.

4 海岸效应的数值模拟研究

4.1 正演模型的建立

地下岩石的电学性质通常用电阻率或电导率来描述.众所周知，地壳浅部为沉积盖层，其电阻率主要取决于岩石的孔隙度和含水量，以及岩石中导电成份的“连通”情况；因而，浅部沉积岩的电阻率一般为101～103Ωm；位于沉积岩层之下的结晶基底，由于埋深增大使岩石所受压力不断增大，导致岩石密度增大，造成结晶基底的电阻率值急剧增加，达103～105Ωm.随着深度进一步增加达中、下地壳，其岩石处于高温高压环境中，温度成为影响岩石电阻率的主要因素，从而导致中、下地壳岩石的电阻率降低.因此，在地壳范围内，地下介质的电性结构由浅部到深部可以粗略地看成是低阻-高阻-低阻的层状模型［6］.近海地区由于受到海洋环境的影响，地表第四纪沉积物发育，近渤海地区地表第四纪沉积物厚度可达几百米［1］，且电阻率一般小于其下部的沉积盖层.

根据地壳电性结构的一般规律和近海地区的地质特征，参考近渤海地区的地质、地球物理资料，将复杂的地下介质电性结构简化为低阻-低阻-高阻-低阻的四层模型.为分析近海地区大地电磁测深方法对异常体的探测能力，在层状模型中嵌入有限延伸的相对高阻异常体和相对低阻异常体，整个电性结构模型处于高导海洋的包围之中（见图1所示）；这即是用于海岸效应数值模拟研究的三维正演模型.

图1a为三维正演模型平面示意图，陆地被海洋所环绕，陆地面积为100km×40km，海水电阻率值为0.33Ωm，测线沿PP′方向，6个大地电磁测深点位于陆地之上.

图1 海岸效应正演计算模型（a）模型俯视图；（b）模型断面示意图.Fig.1 Plan view （a）and vertical cross－section（b）of a three－dimensional forward model

图1b为三维正演模型剖面示意图，地下介质近似于层状电性结构，分为4层，第一层的厚度为0.5km，电阻率为20Ωm；第二层的厚度为1.5km，电阻率为50Ωm；第三层的厚度为28km，电阻率为1000Ωm；第四层由30km深度处开始向下延伸，电阻率为100Ωm.在第三层介质中包含有一个电阻率为200Ωm的相对低阻异常体和一个电阻率为2000Ωm的相对高阻异常体.两个异常体的埋深均为5km，体积为20km×10km×10km.6个大地电磁测深点位于地表，S6测点距离海岸线较近.海水深度根据所研究问题的不同而发生变化.

4.2 海水深度变化的影响

为分析海水深度对近海地区大地电磁测深响应的畸变影响，在图1所示的海岸效应正演模型中选取0、50、100、300、500、1000、2000m7个海水深度，利用有限差分法对上述模型进行三维正演计算，以求取测线PP′上各测点在不同海水深度时的大地电磁测深响应.

图2和图3分别给出了水深50m和1000m条件下测线PP′上6个测点的大地电磁测深响应曲线.

对比图2和图3可知，测线上6个测点均受到了海岸效应的影响，海水深度越大，各测点视电阻率曲线之间的差别越明显，而相位曲线之间的差别均不大.海水深度为50m时，如图2所示，各测点视电阻率曲线在小于0.1Hz的频率范围内有相对较大的差别，且YX模式的视电阻率曲线要比XY模式的视电阻率曲线差别更明显，各测点的相位曲线均十分接近，仅在中频段有细微差别.海水深度为1000m时，如图3所示，各测点的XY模式视电阻率曲线在0.1～0.001Hz的频率范围内明显分开，而YX模式视电阻率曲线在小于0.01Hz的频率范围内彼此之间差别明显，各测点的相位曲线仅在中频段有细小的差别.

由于S6测点与海岸线的距离较近，受海岸效应影响较大，因此，以S6测点为例，分析海水深度变化对大地电磁测深视电阻率曲线和相位曲线的畸变作用，如图4所示.图4中黑色实线表示无海洋存在情况下的大地电磁测深响应曲线，即不受海岸效应影响的大地电磁测深响应曲线，以该曲线为基准来分析不同海水深度对大地电磁测深视电阻率曲线和相位曲线的畸变作用.

图2 海水深度50m时S1—S6大地电磁测深点视电阻率（A）和相位（B）正演响应曲线Fig.2 Apparent resistivity（A）and phase（B）forward responses of S1—S6 with 50mdepth of seawater for the 3Dforward model shown in Fig.1

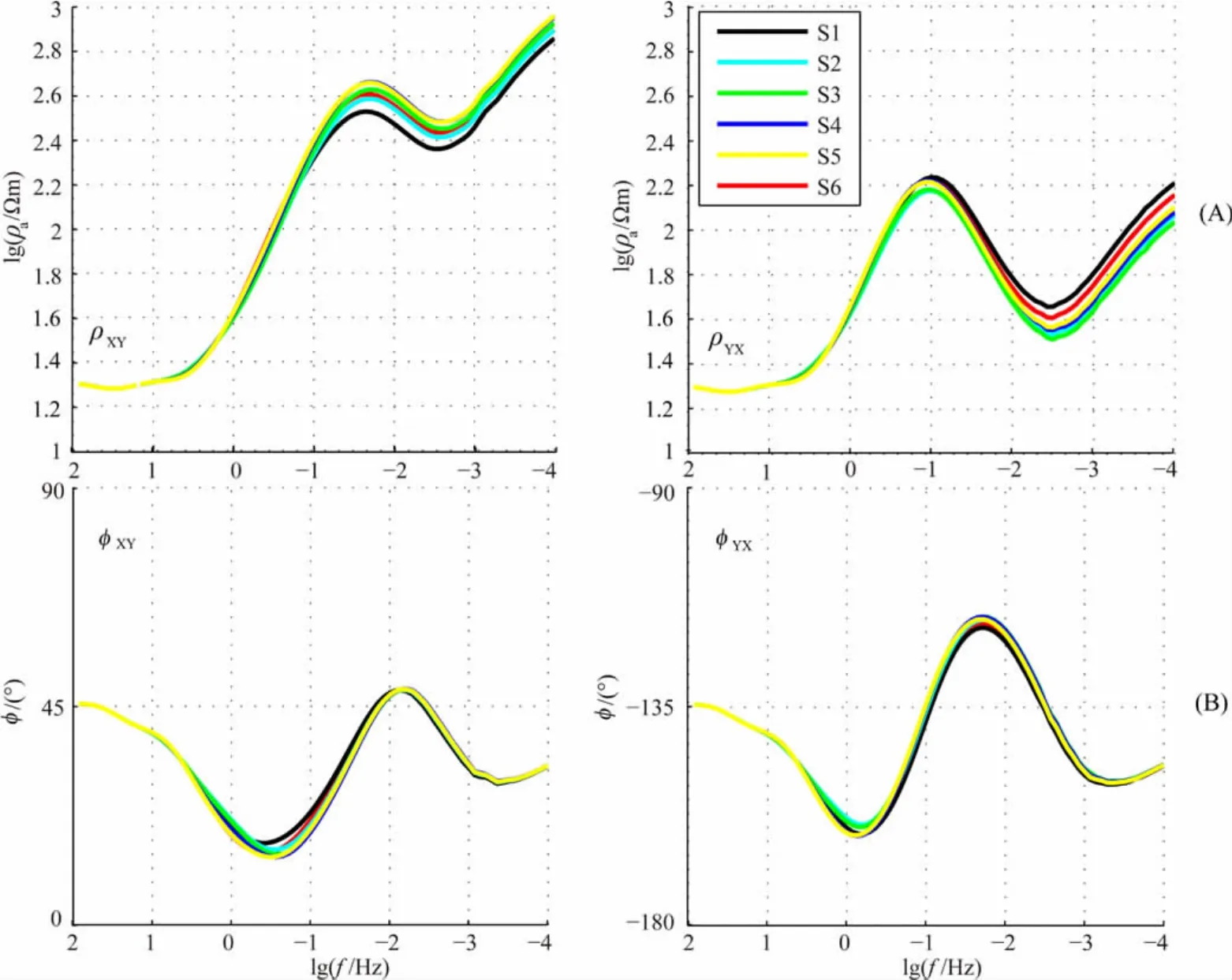
图3 海水深度1000m时S1—S6大地电磁测深点视电阻率（A）和相位（B）正演响应曲线Fig.3 Apparent resistivity（A）and phase（B）forward responses of S1—S6 with 1000mdepth of seawater for the 3Dforward model shown in Fig.1

图4 不同海水深度对S6测点大地电磁测深视电阻率（A）和相位（B）正演响应曲线的影响Fig.4 Apparent resistivity and phase forward responses of S6with different depths of seawater for the 3Dforward model shown in Fig.1

图5 不同海水深度对大地电磁测深一维Occam反演结果的影响（a）水深0m；（b）水深100m；（c）水深500m；（d）水深1000m.Fig.5 1DOccam inversion results of forward responses with 0m（a），100m（b），500m（c）and 1000m （d）depths of seawater

由图4可知，当测点在近海地区时，由于海岸效应的影响，大地电磁测深视电阻率曲线和相位曲线均发生了不同程度的畸变.对于高频段来说，这种畸变十分微弱，大地电磁测深响应曲线基本重合.但对于中、低频段而言，这种畸变严重影响了视电阻率曲线和相位曲线的形态，不可忽视.在中频段，受海水的影响，XY模式的视电阻率值增大，而相位值减小；YX模式的视电阻率值减小，而相位值增大.随着频率的降低，水深变化对大地电磁测深视电阻率曲线和相位曲线的影响规律变得复杂.对于视电阻率曲线来说，以水深100m为界，不同水深条件下的视电阻率曲线形态的变化趋势发生了明显的改变.在0.001Hz左右，水深2km条件下的大地电磁测深响应曲线出现了不规则畸变.

对上述正演计算求取的6个测点的大地电磁测深正演响应数据，利用一维Occam反演算法进行一维反演计算，根据一维反演结果，通过插值计算，绘制测区一维反演拟断面图，如图5所示.图5分别展示了无海洋条件下和100、500、1000m三种水深条件下的一维Occam反演拟断面图.

由图5可知，当无海洋存在时，一维Occam反演拟断面图能够较好地反映出地下介质电阻率的分层信息，且对高阻异常体有较好的探测能力.当测区附近有海水存在时，通过一维Occam反演拟断面图仍能很好地识别浅表地层，这与大地电磁测深资料的高频成分受海岸效应的影响十分微弱相一致.由于高导海水的存在，一维Occam反演结果在深部电阻率值偏大，而且海水越深这种偏差越大，无法反映深部的电性结构信息，这主要是海岸效应对近海地区大地电磁测深数据产生了复杂的畸变作用造成的.

4.3 海底地形变化的影响

为了分析海底地形对近海地区大地电磁测深响应的畸变影响，将图1所示的海岸效应正演模型中的海水层，设计为海水深度由20m到1000m线性渐进变化，利用有限差分法对这种模型进行三维正演计算，求取测线PP′上6个测点的大地电磁测深响应，如图6所示.

图6中实线表示各测点在无海洋存在情况下的大地电磁测深响应，虚线表示各测点受海洋环境影响时的大地电磁测深响应.由图6可知，各测点均受到了海岸效应的影响，海洋的存在使大地电磁测深响应曲线发生了严重的畸变，这种畸变作用主要表现在中、低频段.XY模式视电阻率值在小于0.1Hz的频率范围内明显增大，且频率越低，视电阻率值增大的幅度越大.YX模式视电阻率值在中频段减小，而在低频段增大，且频率越低，视电阻率值增大的幅度越大.两种模式的相位曲线亦在中、低频段出现畸变，当频率小于0.001Hz时，两种模式的相位曲线的变化趋势接近.

以距离海岸线较近的S6测点为例，S6测点的大地电磁测深视电阻率和相位正演响应曲线如图7所示.图7中红色和蓝色的圆圈分别表示渐进海水深度条件下的XY模式和YX模式大地电磁测深响应，而红色和蓝色的实线分别表示无海洋存在时的XY模式和YX模式大地电磁测深响应.

由图7可知，在渐进海水深度条件下，高频段的大地电磁测深响应受海岸效应的畸变作用十分微弱，而低频段的大地电磁测深视电阻率值增大，且XY模式相对于YX模式增加的幅度更大.

阻抗张量元素极化图是指某一频率的阻抗张量元素的模随测量坐标旋转角变化的轨迹.可以用来定性分析地下介质的维度信息［25］.图8是S6测点在海底地形变化时不同频率的大地电磁测深阻抗张量极化图.由图8可知，在浅部，地下介质的一维性质明显，与正演模型相符合.随着深度的增加，地下介质的维度信息变得复杂.在深部，地下介质表现出三维性质，这主要是受到海岸效应的影响造成的.

对反映海底地形变化的6个测点的大地电磁测深正演响应数据，利用一维Occam反演算法进行一维反演计算，根据一维反演结果，通过插值计算，绘制测区一维Occam反演拟断面图，如图9所示.

由图9可知，当海底地形变化时，一维Occam反演拟断面图能够较好地反映出地下浅层介质的电性结构，深部地层的反演结果电阻率值偏大，但仍能反映出层状结构的趋势，且对高阻异常体有较好的探测能力.这一结果与大地电磁测深资料的高频成分受海岸效应的影响十分微弱，而低频成分易受海岸效应的影响而发生畸变相关联.

对反映海底地形变化的6个测深点的大地电磁测深正演响应数据，利用二维非线性共轭梯度（NLCG）反演算法进行二维反演计算，该测区的TM模式、TE模式、TM和TE联合模式、TM、TE以及HZ联合模式的二维反演结果如图10所示.

由图10可以看出，4种反演模式均能够反映出浅部地层的电性结构，其中TM模式对浅部地层的反演效果最好.TM模式的反演结果能够在一定程度上反映出高阻异常体和低阻异常体的存在，在海岸线附近5～20km深度范围内电阻率值偏大，深部出现了大面积的低阻假异常.TE模式的反演结果对高阻异常体的存在有一定的反映，对低阻异常体的探测效果不明显.深部地层的TE模式反演结果较为可靠.两种联合模式的反演结果包含了TM模式和TE模式各自的优、缺点.联合模式反演结果对高阻异常体和低阻异常体均有一定的反映，但在距离海岸线较近的区域出现高阻假异常，在深部则出现低阻假异常.TM模式反演对介质中三维电性结构的适应性较强.在地表存在不均匀体，静位移［26］影响严重的情况下，TE模式通常具有较好的反演效果.

图6 渐变海水深度条件下海岸效应对S1～S6大地电磁测深点视电阻率（A）和相位（B）正演响应曲线的影响Fig.6 Apparent resistivity and phase forward responses of S1～S6station for the 3Dforward model shown in Fig.1

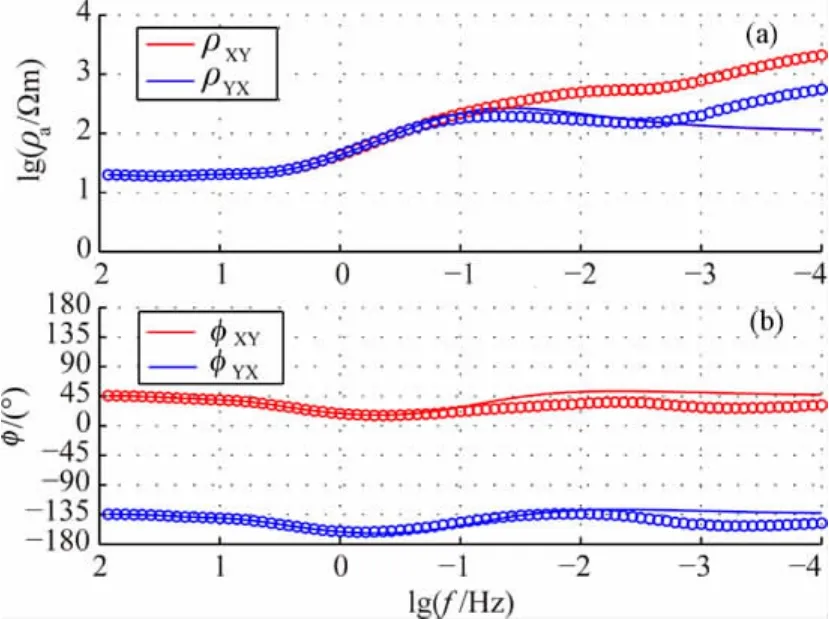
图7 渐变海水深度条件下S6测点大地电磁测深视电阻率（a）和相位（b）正演响应曲线Fig.7 Apparent resistivity（a）and phase（b）forward responses of S6station for the 3Dforward model shown in Fig.1

5 近海地区实测大地电磁测深数据质量分析

在北纬39°东经117°的近渤海地区进行了大量的大地电磁测深野外采集工作，如图11所示.渤海深度较浅，小于30m的海域近7.2×104km2，海底地势平坦，地形也较为单调.渤海为中、新生代沉降盆地，基底为前寒武纪变质岩.第四纪的沉积厚度约300～500m.地壳厚度，中部为29km，向四周增加，可达31～34km［1］.

由于图11所示的大地电磁测深点分布在近海地区，海岸效应影响严重，需要详细评估测区测点的数据质量.以距离渤海较近的B1号大地电磁测深点为例，分析近渤海地区实测大地电磁测深数据的数据质量.野外数据采集所使用的仪器是加拿大凤凰公司生产的MTU5大地电磁采集系统.野外采集Ex、Ey、Hx、Hy、Hz五个电磁场分量，频率范围为320～0.0001Hz.对实测的大地电磁测深数据进行远参考处理和功率谱挑选，以改善数据质量，提高信噪比.B1测点的大地电磁测深响应曲线图和阻抗张量极化图如图12所示.

图8 渐变海水深度条件下S6测点不同频率大地电磁测深阻抗张量极化图Fig.8 Impedance polar diagrams of S6station as a function of frequency for the 3Dforward model shown in Fig.1

从图12可以看出，大地电磁测深响应曲线在高频部分受到畸变作用影响较小，XY模式和YX模式视电阻率曲线基本重合，与浅表地层的一维沉积盖层性质相对应，浅表介质的一维性质在维度参数曲线和阻抗张量极化图中也有明显的显示.在中频部分，大地电磁测深视电阻率和相位均受畸变作用影响严重，不能可靠地反映地下介质的电阻率信息，这种畸变可能是由于噪声干扰的影响造成的.对于低频部分来说，XY模式和YX模式的两条大地电磁测深视电阻率曲线明显分开，指示出地下介质的复杂结构，阻抗张量极化图也反映出地下介质明显的三维性质，但是这种结果也可能是由于测点位于近海地区，受海岸效应的影响而发生畸变引起的.

对B1号大地电磁测深点的实测数据，利用一维Occam反演算法进行反演计算，B1测点处的一维Occam反演结果如图13所示.由图13可知，TE模式对B1测点的视电阻率曲线和相位曲线的拟合效果均较好，而TM模式仅对B1测点的视电阻率曲线拟合的效果较好.在低频段，TM模式的一维Occam反演结果无法拟合B1测点的相位曲线.综合分析TE模式和TM模式一维Occam反演所得出的B1测点处的一维介质模型可知，浅表地层的电阻率较低，在深度大于1km的地层中，介质的电阻率开始有所增大，在1～10km的深度范围内可能存在有高阻层.

6 结论和建议

本文通过正演模拟方法，分析和总结了海水深度变化和海底地形变化对近海地区大地电磁测深数据的畸变影响.当测点位于近海地区时，由于海岸效应的影响，大地电磁测深视电阻率曲线和相位曲线均会发生不同程度的畸变.在高频部分，这种畸变影响十分微弱.而在低频部分，这种畸变严重影响了视电阻率曲线和相位曲线的形态，海岸效应不可忽视，会直接影响到大地电磁测深资料的处理解释结果.对近海地区大地电磁测深数据进行一维Occam反演和二维NLCG反演，两者对浅表地层均具有较好的反演效果，这与大地电磁测深资料的高频成分受海岸效应的影响十分微弱相一致.随着海水深度的增加和海底地形的复杂变化，一维和二维反演结果在深部均会出现不同程度的假异常，为地质解释工作造成了影响.由于海岸效应的影响，一维Occam反演结果深部电阻率值偏大.二维NLCG反演TM模式对表层结构敏感，易受静位移的影响，而TE模式对深部结构的反映更可靠.近渤海地区的实测大地电磁测深数据在低频部分可能受到海岸效应的影响而导致视电阻率曲线和相位曲线的严重畸变.

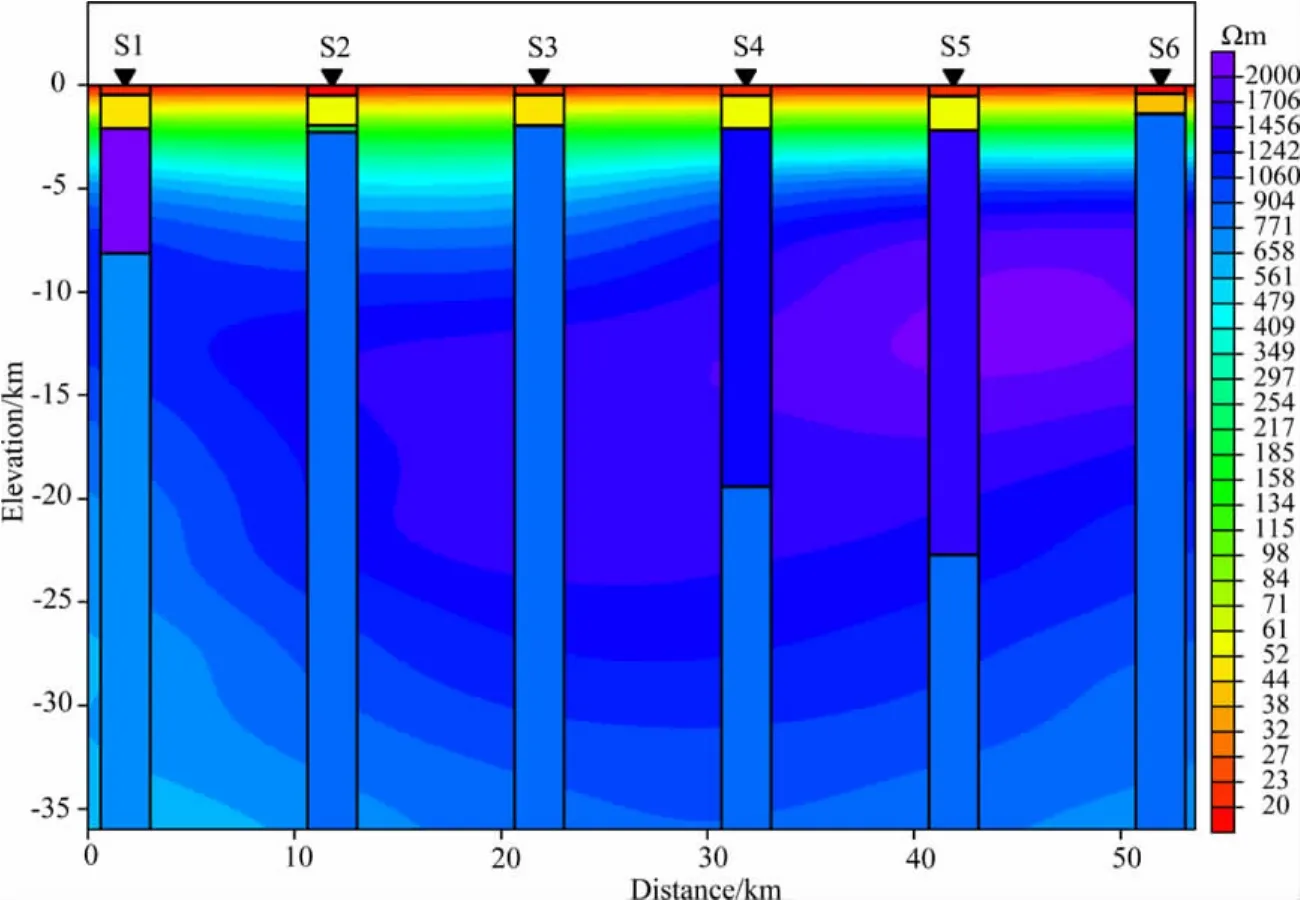
图9 渐变海水深度条件下大地电磁测深一维Occam反演拟断面图Fig.9 1DOccam inversion results of forward responses for the 3Dforward model shown in Fig.1

图10 渐变海水深度条件下大地电磁测深二维非线性共轭梯度反演结果（a）TM 模型；（b）TE模式；（c）TM ＆ TE联合模式；（d）TM ＆ TE ＆ HZ联合模式.Fig.10 2DNLCG inversion results of forward responses for the 3Dforward model shown in Fig.1（a）Mode TM；（b）Mode TE；（c）Mode TM ＆ TE；（d）Mode TM ＆ TE ＆ HZ.

图11 实测大地电磁测深数据点位示意图Fig.11 Map of the survey area with MT sounding stations

图12 B1测点大地电磁测深响应曲线图和阻抗张量极化图Fig.12 MT response curves and impedance polar diagrams of B1station

在近海地区进行大地电磁测深资料的处理解释时，忽略海岸效应的影响，将对地质解释工作造成巨大困难.建议对近海地区更加复杂的地质模型进行分析，进一步总结海岸效应对近海地区大地电磁测深数据的畸变作用.

图13 B1测点大地电磁测深一维Occam反演模型（A）TE模式；（B）TM 模式；（a1，b1）视电阻率；（a2，b2）相位；（a3，b3）一维模型.Fig.13 1Dmodel of B1station with 1DOccam inversion

（References）

［1］冯士筰，李凤岐，李少菁.海洋科学导论.北京：高等教育出版社，1999.Feng S Z，Li F Q，Li S J.An Introduction to Marine Science（in Chinese）.Beijing：Higher Education Press，1999.

［2］李桐林，林君，王东坡等.海陆电磁噪声与滩海大地电磁测深研究.北京：地质出版社，2001.Li T L，Lin J，Wang D P，et al.The Oceanic and Terrestrial Noise and Shallow Marine Magnetotelluric Study（in Chinese）.Beijing：Geological Publishing House，2001.

［3］Parkinson W D.Directions of rapid geomagnetic fluctuations.Geophys.J.R.Astr.Soc.，1959，2（1）：1－14.

［4］Parkinson W D.The influence of continents and oceans on geomagnetic variations.Geophys.J.R.Astr.Soc.，1962，6（4）：441－449.

［5］Jones F W，Price A T.The perturbations of alternating geomagnetic fields by conductivity anomalies.Geophys.J.R.Astr.Soc.，1970，20（3）：317－334.

［6］Parkinson W D，Jones F W.The geomagnetic coast effect.Reviews of Geophysics，1979，17（8）：1999－2015.

［7］Nolasco R，Tarits P，Filloux J H，et al.Magnetotelluric imaging of the Society Islands hotspot.J.Geophys.Res.，1998，103（B12）：30287－30309.

［8］杨文采，方慧，程振炎等.苏鲁超高压变质带北部地球物理调查（II）——非地震方法.地球物理学报，1999，42（4）：508－519.Yang W C，Fang H，Cheng Z Y，et al.Geophysical investigation of Northern Sulu UHPM Terrane in East China（II）：Non－seismic Methods.Chinese J.Geophys.（in Chinese），1999，42（4）：508－519.

［9］Snatos F M，Nolasco M，Almeida E P，et al.Coast effects on magnetic and magnetotelluric transfer functions and their correction：application to MT soundings carried out in SW Iberia.Earth Planet.Sci.Lett.，2001，186：283－295.

［10］Yang J M，Min D J，Yoo H S.Sea effect correction in magnetotelluric（MT）data and its application to MT soundings carried out in Jeju Island，Korea.Geophys.J.Int.，2010，182：727－740.

［11］Chave A D，Thomson D J.Bounded influence magnetotelluric response function estimation.Geophys.J.Int.，2004，157（3）：988－1006.

［12］McNeice G W，Jones A G.Multisite，multifrequency tensor decomposition of magnetotelluric data.Geophysics，2001，66（1）：158－173.

［13］Baba K，Chave A D.Correction of seafloor magnetotelluric data for topographic effects during inversion.J.Geophys.Res.，2005，110：B12105，doi：10.1029／2004JB003463.

［14］Matsuno T，Seama N，Baba K.A study on correction equations for the effect of seafloor topography on ocean bottom magnetotelluric data.Earth Planets Space，2007，59（8）：981－986.

［15］Nam M J，Kim H J，Song Y，et al.Three－dimensional topography corrections of magnetotelluric data.Geophys.J.Int.，2008，174（2）：464－474.

［16］Mackie R L，Bennett B R， Madden T R.Long-period magnetotelluric measurements near the Central California Coast：a land－locked view of the conductivity structure under the Pacific Ocean.Geophysical Journal，1988，95（1）：181－194.

［17］Fischer G.Electromagnetic induction effects at an ocean coast.Proceedings of the IEEE，1979，67（7）：1050－1060.

［18］Simpson F，Bahr K.Practical Magnetotellurics.Cambridge：Cambridge University Press，2005.

［19］Unsworth M，Soyer W，Tuncer V，et al.Hydrogeologic assessment of the Amchitka Island nuclear test site（Alaska）with magnetotellurics.Geophysics，2007，72（3）：B47－B57.

［20］Mackie R L，Smith J T，Madden T R.Three－dimensional electromagnetic modeling using finite difference equations：The magnetotelluric example.Radio Science，1994，29（4）：923－935.

［21］胡祖志，胡祥云.大地电磁三维反演方法综述.地球物理学进展，2005，20（1）：214－220.Hu Z Z， Hu X Y. Review of three dimensional magnetotelluric inversion methods.Progress in Geophysics（in Chinese），2005，20（1）：214－220.

［22］胡祖志，胡祥云，何展翔.大地电磁非线性共轭梯度拟三维反演.地球物理学报，2006，49（4）：1226－1234.Hu Z Z，Hu X Y，He Z X.Pseudo－Three－Dimensional magnetotelluric inversion using nonlinear conjugate gradients.Chinese J.Geophys.（in Chinese），2006，49（4）：1226－1234.

［23］Constable S C，Parker R L，Constable C G.Occam′s inversion：A practical algorithm for generating smooth models from electromagnetic sounding data.Geophysics，1987，52（3）：289－300.

［24］Rodi W， Mackie R L. Nonlinear conjugate gradients algorithm for 2－D magnetotelluric inversion.Geophysics，2001，66（1）：174－187.

［25］石应骏，刘国栋，吴广耀等.大地电磁测深法教程.北京：地震出版社，1985.Shi Y J，Liu G D，Wu G Y，et al.Magnetotellurics（in Chinese）.Beijing：Seismological Press，1985.

［26］Young C T，Kitchen M R.A magnetotelluric transect in the Oregon coast range.J.Geophys.Res.，1989，94（10）：185－193.