一种适于镜面反射表面的从明暗恢复形状算法

王国珲，苏 炜，宋玉贵

(西安工业大学光电工程学院，陕西 西安 710032)

从明暗恢复形状(Shape－from－Shading，SFS)是计算机视觉中实现物体表面三维形状重构的关键技术之一。SFS方法通过求解建立的单幅图像的辐照度方程来获取物体表面各点的法向量或相对高度，其技术原理简单，应用非常广泛［1］。

SFS方法最早是由麻省理工学院的Horn学者在20世纪70年代提出的［2］，在此基础上，经过几十年的发展，出现了很多新的算法［3－6］，如:文献［2 －3］将 SFS 方法中的辐照度方程转化为能量函数形式，然后附加一定的约束条件将其变换为泛函极值求解问题;文献［4］将SFS问题中原先的非线性反射图方程转化为线性问题，从而方便计算辐照度方程的解;文献［5－6］对SFS问题建立的一阶非线性偏微分方程本身直接求解，从图像中一组已知高度值的初始点出发，逐步确立出图像中所有像素点对应的物体表面的三维形状。上述SFS方法存在着两方面的问题:一是使用的反射模型通常为Lambert模型，这样虽可以简化计算，然而对于非Lambert表面(如镜面反射表面)通常会引起较大的重构误差;二是采用的数值算法往往通过迭代形式实现，算法运行时间较长，达不到快速重构的要求［7］。

为了实现镜面反射表面快速重构的需求，本文提出了一种基于高阶Fast Marching方法的SFS算法，解决了上述几个不足。本文提出的SFS算法有下面两个特点:1)使用Blinn－Phong模型刻画镜面反射表面的反射特性，这样更适于镜面反射表面的实际情况，减少了由于模型误差引起的重构精度不高问题;2)将基于Blinn－Phong模型的镜面表面图像辐照度方程转化为含有高度信息的Eikonal偏微分方程，利用高阶Fast Marching方法计算上述Eikonal方程的解，在获得二阶精度的同时减少了算法的运行时间。

1 基于Blinn－Phong模型的辐照度方程

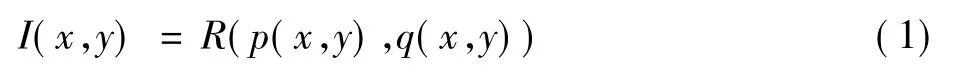
假定摄像机的成像平面为x－y平面，摄像机的光轴与z轴重合。在上述坐标系下，SFS问题可以看作是求解如下图像辐照度方程［7－8］式中:I(x，y)为图像的灰度值，亦认为是图像的辐照度;R(p(x，y)，q(x，y))是由物体表面反射模型确立的反射图，它描述了光源分布与物体表面方向的对应关系。在正交投影条件下，通常使用下式来计算物体表面一点(x，y，z(x，y)) 的方向向量

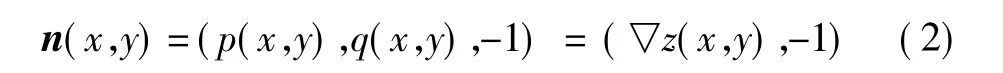
如图1所示的表面反射几何模型，已知点光源的单位方向向量为L，摄像机的单位方向向量为V;θi，φi和θr，φr分别为光源、摄像机方向向量的天顶角和方位角。对于镜面反射表面，Phong［9］提出了一个经验模型，用来计算镜面反射表面的辐射亮度

式中:M为镜面反射指数;R为反射光的单位方向向量，且有R=2×n(n·L)－L。

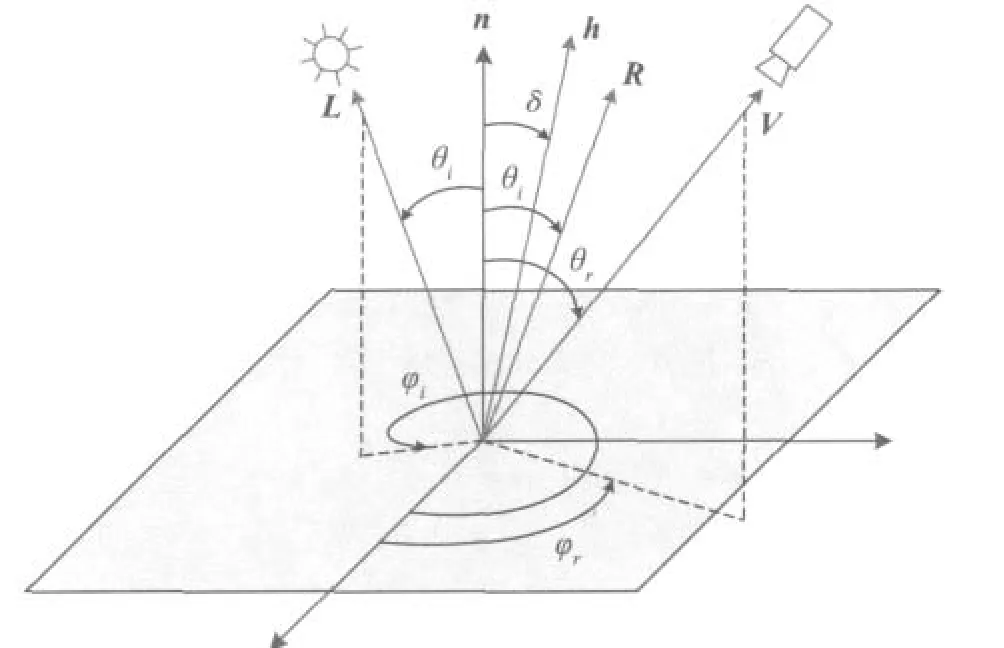
图1 表面反射几何模型

鉴于Phong模型在实际应用时，计算(R·V)不方便，Blinn［10］对Phong模型进行了改进，用(n·h) 来代替(R·V)，简化了运算。Blinn－Phong模型为

式中，h为光源方向向量L与摄像机方向向量V之间夹角平分线的单位方向向量。本文使用Blinn－Phong反射模型来近似其反射属性，可以得到镜面反射表面的图像辐照度方程为

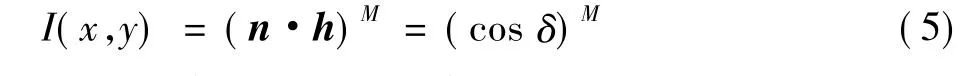
式中，δ为n与h之间的夹角。

假定光源与摄像机共线，此时有θi=θr，φr=φi，因此 δ= θi。设光源的方向向量为［0，0，－1］，由于θi为n与L之间的夹角，故有

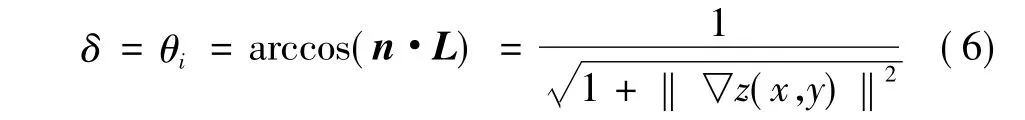
将式(6)代入(5)，得到基于Blinn－Phong模型的图像辐照度方程

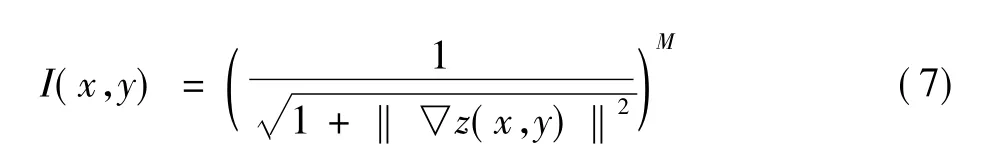
2 图像辐照度方程求解

为了求解图像辐照度方程(7)，一种直接的方法就是将其转化为含有高度信息的Eikonal偏微分方程(8)，应用相关数值方法进行求解

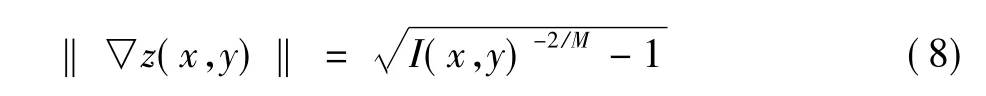
考虑图像大小为(1，m)×(1，n)的均匀离散网格点:(xi，yj)=(iΔ，jΔ) ，i=1，2，…，m ，j=1，2，…，n，(Δ，Δ)为数值算法中离散网格的大小。本文中数值方法的目的就是求解高度函数 z(x，y) 的离散近似解 zi，j=z(xi，yj)。

在作者以前的研究工作中，求解Eikonal方程的算法使用到高阶 Fast Sweeping方法［8］及 Fast Marching方法［11］。高阶Fast Sweeping方法虽然可以获取较高的重构精度，但算法需要迭代，故运行时间较长，达不到快速重构的要求;而Fast Marching方法虽运行时间较短，但重构精度较低。考虑到快速精确性的要求，本文使用文献［12］提出的高阶Fast Marching方法来逼近上述Eikonal方程(8)的解。

传统的Fast Marching方法是一种一阶精度的、非迭代(单步)的复杂度为O(NlogN)的数值方法，其中N为离散网格的总数。对Eikonal方程(8)，利用单调迎风Hamilton函数逼近有

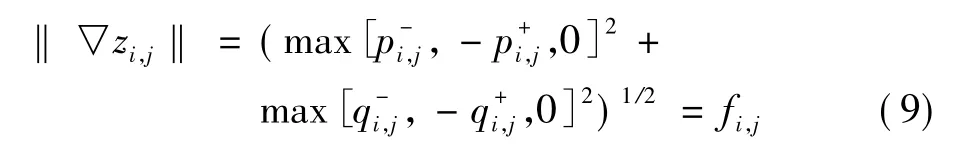
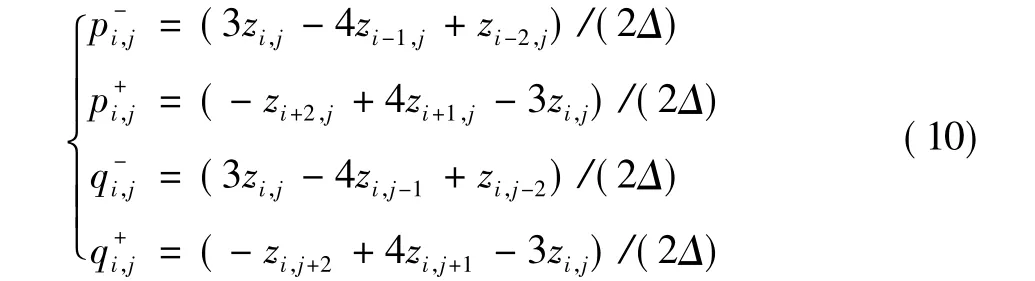
将式(10)代入(9)，可以得到二阶精度的‖▽zi，j‖逼近。

于是，基于高阶Fast Marching方法的适于镜面反射表面的从明暗恢复形状算法过程如下:

1)初始化

(1)设置网格点标志:设置初始点的标志为K;将标志为K的像素点的8个邻域的标志设为T;剩余网格点的标志设置为F。

(2)将所有标志为K的网格点的值设定为真实高度值，作为Marching过程的初始高度值，而且在整个Marching过程中不发生变化;标志为T的网格点的值由初始高度值与邻域的位置确定;所有标志为F的网格点的值设定为无穷大。T和F网格点的值在Marching过程中将得到重新计算。

2)选择 (iminΔ，jminΔ) 为 T 中 z值最小的点，并将(iminΔ，jminΔ)点从T中移出并添加到K中。

3) 考虑 (iminΔ，jminΔ) 的 8 个邻域 (imin－1Δ，jminΔ) ，(imin－2Δ，jminΔ) ，(imin+1Δ，jminΔ) ，(imin+2Δ，jminΔ) ，(iminΔ，jmin－1Δ) ，(iminΔ，jmin－2Δ) ，(iminΔ，jmin+1Δ) ，(iminΔ，jmin+2Δ)中不为K的点:

(1)若(iminΔ，jminΔ)的邻域标志为F，将其从F中移出并添加到T中，并用式(9)更新其值。

(2)若(iminΔ，jminΔ)的邻域标志为T，则直接用式(9)更新其值。

4)当所有网格点的标志均为K时，算法结束，否则返回步骤2)。

3 实验验证

为了验证本算法的性能，使用两幅已知高度的镜面反射表面图像进行验证，高度图和图像如图2所示，重构结果如图3所示。图2a与2b分别为圆柱体、花瓶的三维高度图，图2c与2d为获取的对应的图像。由图2c与2d可以看出，图像中含有高光，为镜面反射表面形成的图像。图3a与3b分别为本算法重构的三维形状。对于圆柱体图像和花瓶图像，本算法的运行时间均为0.02 s左右。图3c与3d为圆柱体、花瓶的高度误差图。为了定量评价本算法的重构结果，使用高度平均绝对误差(Mean Absolute Error，MAE)和均方根误差(Root Mean Square Error，RMSE)来反映其精确度。高度MAE和RMSE分别定义为

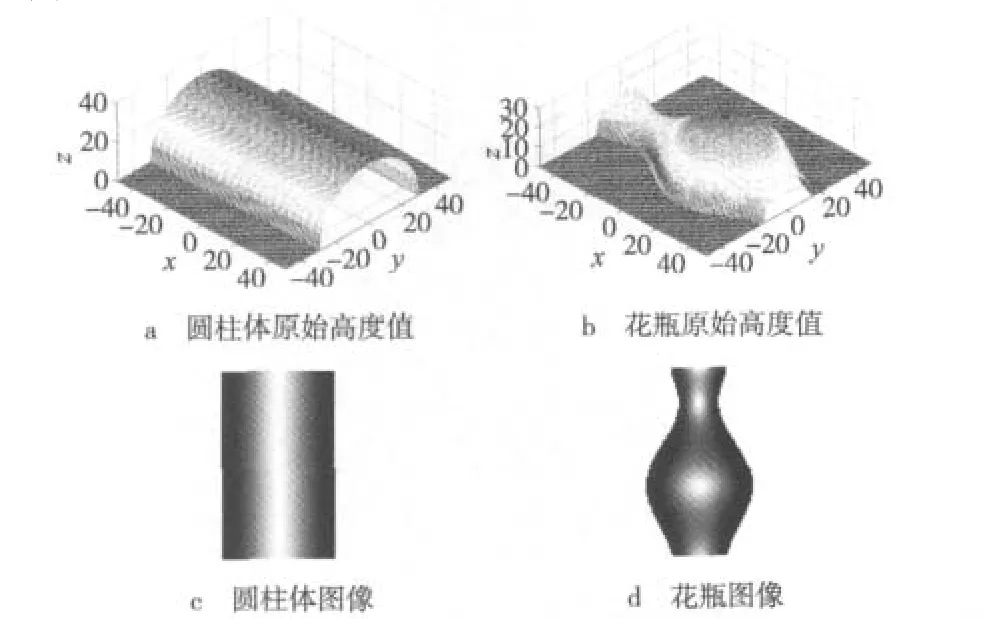
图2 高度图及图像

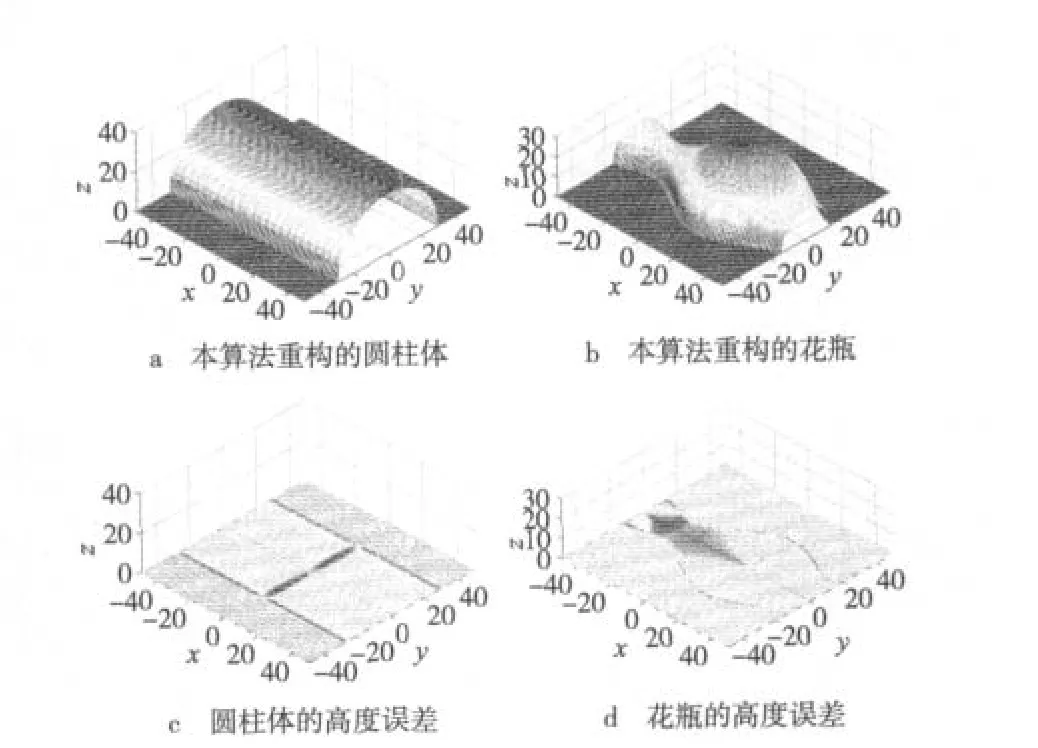
图3 重构结果

4 小结

本文提出了一种基于高阶Fast Marching方法的从明暗恢复形状算法，可以实现镜面反射表面快速重构的需求。首先假定光源为点光源，且位于无穷远处，同时摄像机遵循正交投影，其方向与光源方向保持一致;其次使用Blinn－Phong模型来描述镜面反射表面的反射特性，减少了由于模型误差引起的重构精度不高问题;建立基于Blinn－Phong反射模型的镜面表面图像辐照度方程，然后将该辐照度方程转化为含有高度信息的Eikonal偏微分方程，利用高阶Fast Marching方法计算上述Eikonal方程的解，从而获得镜面反射表面的三维形状，在获得二阶精度的同时减少了算法的运行时间。经圆柱体和花瓶图像实验，结果表明本文提出的方法可以快速精确地实现镜面反射表面的三维重构。

［1］王国珲，韩九强，张新曼，等.一种从混合表面的明暗变化恢复形状的新算法［J］. 宇航学报，2011，32(5):1124－1129.

［2］HORN B K P.Height and gradient from shading［J］.International Journal of Computer Vision，1990，5(1):37－75.

［3］HORN B K P，BROOKS M J.The variational approach to shape from shading［J］.Computer Vision，Graphics，and Image Processing，1986，33(2):174－208.

［4］TSAI P－S，SHAH M.Shape from shading using linear approximation［J］.Image and Vision Computing，1994，12(8):487－498.

［5］PRADOS E，FAUGERAS O.A generic and provably convergent shapefrom－shading method for orthographic and pinhole cameras［J］.International Journal of Computer Vision，2005，65(1/2):97－125.

［6］ZHANG L，YIP A M，BROWN M S，et al.A unified framework for document restoration using inpainting and shape－from－shading［J］.Pattern Recognition，2009，42(11):2961－2978.

［7］王国珲，韩九强，张新曼.一种适合漫反射表面从明暗恢复形状的快速算法［J］.西安交通大学学报，2009，43(10):7－10.

［8］WANG Guohui，SU Wei，SONG Yugui.A new shape from shading approach for specular surfaces［J］.Lecture Notes in Computer Science，2011，7004:71－78.

［9］PHONG B T.Illumination for computer generated pictures［J］.Communications of the ACM，1975，18(6):311－317.

［10］BLINN J F.Models of light reflection for computer synthesized pictures［J］.ACM SIGGRAPH Computer Graphics，1977，11(2):192－198.

［11］WANG Guohui，SU Wei，GAO Fen.A specular shape from shading by fast marching method［J］.Procedia Engineering，2011(24):192－196.

［12］SETHIAN J A.Fast marching methods［J］.SIAM review，1999，41(2):199－235.