基于高斯随机性的弹道轨迹仿真
刘宏义,肖 瑜
(中国人民解放军边防学院信息化研究实验室,陕西 西安 710108)
一个非常流行的高质量GRNG是polar-rejection[2]。这个算法因被《Numerical Recipes in C》[97年出版]一书采录而流行,并因为它最费时的操作只有一个对数操作和一个平方根操作而著名(它规避了最初Box-Mueller变换中所需要的sin和cos操作)。虽然这是一个很好的GRNG,但是还有更快的算法。Ziggurat方法[3]是第二流行的GRNG,并经常被列为在速度和质量的平衡上做得最好的算法[6]。它比polar-rejection算法要快,因为它使用了一个大小为1 kB的查询表并且极少调用超越函数。但是,对于游戏开发来说,访问这些查询表会污染数据缓存,从而导致实际运行比使用polar-rejection反而更慢。因为在大多数平台上相对于CPU的速度,访问内存的代价很高。举例来说,当Ziggurat方法在高速执行,它的查询表就会将游戏程序中的其他数据挤出缓存,从而减缓整个游戏的速度,相对polar-rejection更甚。以上两种方法对于游戏程序都不太合适,最佳的方法是一种简单高效的技术,被称为中心极限定理(central limit theorem),有时候也被叫作均匀数和(sum-of-uniforms)[6]。这个算法采用一些均匀随机数,比如,一些由一个像rand()这样的PRNG产生的随机数,并将它们相加。根据中央极限定理,这些均匀随机数的和将产生一个高斯分布随机数。
1 高斯随机性生成算法
中央极限定理指出K个在区间[-1,1]均匀随机数的和将逼近一个以0为中心、标准偏差为的高斯分布。比如说,如果你将3个均匀随机数相加,它们的分布将以0为中点,标准偏差=1.0(这样非常便利,因为中点和标准偏差与一个标准的正态分布一致)。以下的伪代码通过将3个32位的带符号随机数(通过一个非常快速的异或移位PRNG[4]生成)相加来生成一个高斯分布。


函数gaussrand()返回一个区间[-3.0,3.0]内的双精度数。如果想要一个在区间[-1.0,1.0]内的数,只需简单地将结果除以3.0(这会相应地将标准偏差收缩为0.33)。这个分布大致遵守68-95-99.7法则,但由于分布的尾部丢失,这个特定算法的分布实际是66.7-95.8-100。
对更多的数值(增加K)求和可使中心极限定理方法更为精确,尤其是在3个标准偏差之外的尾部。但是,这会使得算法更慢而又没有太大的好处,因为通常并不关心尾部。
2 高斯分布
像rand()这样的随机数生成器可以产生均匀分布,在给定范围中任意一个给定数字都将以相同(或者均匀)的概率出现。比如,在区间[0,1],得到0.3和0.6的概率是一样的。而高斯分布有时也被称为正态分布,倾向于以0为中心附近的正负数。当这个分布的标准偏差为1.0时,我称之为标准正态分布,如图1所示。这个分布也经常因它的形状被称为钟形曲线。
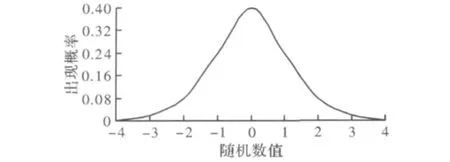
图1 钟形曲线
图1是以0为中点,标准偏差为1.0的高斯分布。水平轴表示所生成的随机数值,而竖直轴表示任意特定值的出现概率,这个分布的尾巴是3个偏差之外的极小概率出现的数值(<-3.0或>3.0)。为更好地理解该图,需要了解68-95-99.7法则。根据这个法则,68%的值将落在距离中点一个标准偏差的区间[-1,1],95%的值落在两个标准偏差区间[-2,2],而99.7%的值落在3个标准偏差区间[-3,3]区间。其余的0.3%落在这个区间之外,而得到在±4.0之外的数字只有少于百万分之一的概率。
3 模拟弹道轨迹
无论是开枪射击或者是射箭,目标靶上的弹着点总是散布在靶心周围,只有个别点偏离得很远。这类弹着点分布不是由rand()产生的,它是一种特殊的随机性。研究发现有一些随机数生成器可产生这类散布现象,这就是非常高效的高斯随机数生成器。
在军事游戏GRNG的一个理想应用就是为发射轨迹加上随机变动。如上所述,发射物体,像子弹和箭都遵循高斯分布的变动。但是,所用的高斯分布必须拓展到2D,如图2所示。
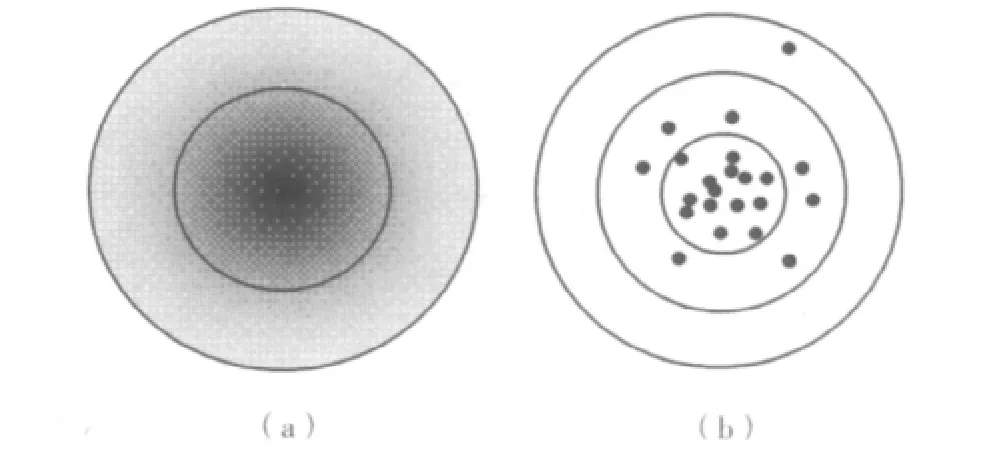
图2 弹着点的高斯分布图
在图2(a)展示了一个在2D中的高斯概率分布。图2(b)是一个30发子弹 一个高斯分布的扰动图。因为这些圆环是以一个和两个标准偏差距离摆放的,所以基本上68%的弹点在最小的环内,而95%的弹点在第二小的环内图2中的分布是使用极坐标生成的。这样每个2D点就需要两个随机数:一个角度和一个距离。在图2中的子弹是这样产生的:先生成一个区间[0,2π]内均匀随机的角度,然后生成一个区间[-1,1]内的高斯随机数,取其绝对值作为距离。通过使用一均匀随机数作为角度,可以确保子弹均匀分布在中心周围的各个角度上。而使用一个高斯随机数作为距离,就可以确保子弹都集中在中心附近,遵守一个正态分布和68-95-99.7法则。
图2中的2D分布从技术上来说并不是一个2D高斯分布。一个真正的2D高斯分布是通过两个高斯随机数在笛卡儿坐标下描点绘制出来。这个分布在统计中很有用,但并不适合弹道轨迹的建模。
4 高斯随机性的其他应用
高斯随机性不仅可应用于弹道轨迹变化,也可以应用在其他游戏领域。比如说,有多个人物或者车辆在一起移动,可能会看见步调一致的移动,这时可以将各个个体的加速度、最大速度或者动画速度通过使用一个GRNG来扰乱开从而避免。这样就可以产生一些在平均值附近的小差异来破坏同步的移动或者动画。结果只会产生很小的差异,并且极少的例外。
GRNG的另一个应用是用来扰乱各个人物、树或者建筑的高度。如果通过算法控制游戏中的几何物体,那使用一个GRNG就可以产生很真实的差异。当游戏每时每刻都可以看见的很多物体,你又需要很自然的差异化时,这个方法就非常有用。通常,许多物理特性或者属性都是在一个平均值附近随机变化的。如果使用高斯分布来模拟,都会有较好的效果。
为什么许多自然中的分布都遵循高斯分布呢?比如人类智商或者树的高度?中心极限定理给了暗示。当有许多均匀的随机因素作用于一个给定的属性时,这个属性的分布将变得更为正态。虽然这只是自然界中大多数系统的一个粗略简化,但这阐明了这么多属性和系统大致展现出高斯分布的原因。可以将自然界中的许多属性大致归结为许多小的、相对独立的因素叠加作用于一个给定的属性。
5 结束语
通过中心极限定理为游戏生成高斯随机性是相当简单和高效的。但许多游戏程序员甚至都不知道这类随机数生成器,因此,最大的挑战在于简单地将方法描述出来,并让开发人员了解到这个工具的存在。许多倾向于具有正态分布的物理系统和特性都可以使用高斯随机性来建模。通过在极坐标中组合均匀随机性和高斯随机性,仿真像弹道轨迹的变动是可以轻松实现的。
[1]BOX G E P,MULLER M E.A note on the generation of random normal deviates[J].The Annals of Mathematical Statistics,1958,9(2):610 -611.
[2]KNOP R.Remark on algorithm 334[g5]:normal random deviates[J].Commun.ACM,1969,12(5):31 -36.
[3]MARSAGLIA G,TSANG W W.The ziggurat method for generating random variables[J].Journal of Statistical Software,2000(5):1001-1008.
[4]MARSAGLIA,GEORGE.Xorshift RNGs[J].Journal of Statistical Software,2003(8):291 -294.
[6]PRESS W H,TEUKOLSKY S A,VETTERLING W T,et al.Numerical recipes in C[M].2nd edition.Cambridge:Cambridge University Press,1997.
[6]THOMAS D B,LEONG P G W,LUK W,et al.Gaussian random numbergenerators [C].ACM ComputingSurveys 39,2007.

