SVM及其鲁棒性研究

吉卫卫，谭晓阳

(南京航空航天大学计算机科学与技术学院，江苏 南京 210016)

支持向量机(SVM)是借助于最优化方法解决数据挖掘中若干问题的有力工具，所得分类器的复杂度可采用支持向量的个数，而不是变换空间的维数来刻划，因此它在一定程度上克服了“维数灾难”和“过学习”等传统困难。并在诸多领域有成功的应用［1］。

文中针对图像中含有类别噪声［2］的人脸识别问题，证明SVM本身对噪声具备一定的鲁棒性。通过调节目标函数中的正则化参数，能够尽量减少噪声的影响。丢弃部分被判定为噪声的样本将进一步改善性能。PubFig数据集上的实验证明，当噪声率低于约40%时，算法仍有效。

1 SVM方法及其鲁棒性

文中的目标类别识别为二分类问题:给定一个测试图像x，预测其目标类别的概率。用SVM作为分类器模型，训练一个支持向量机的目标是找到一个具有最大间隔的分隔平面。支持向量是那些到平面距离最近的模式。非线性情况下SVM的目标函数如下:

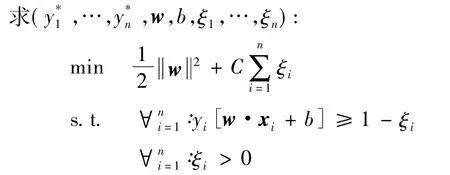
其Lagrange函数为

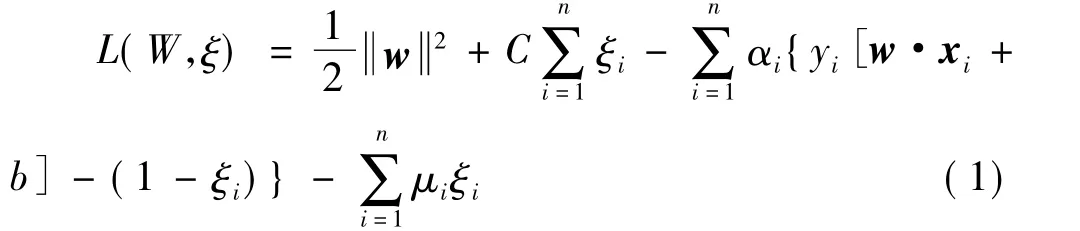
分别对W和ξ求导

将 W、αi代入L(W，ξ)得其对偶表示为

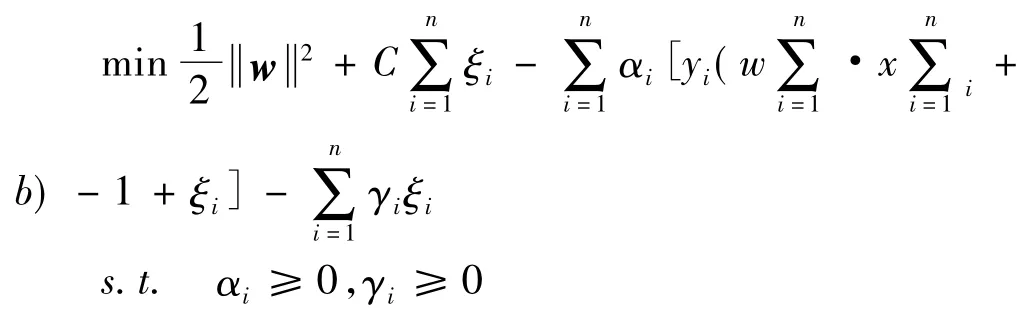
KKT条件

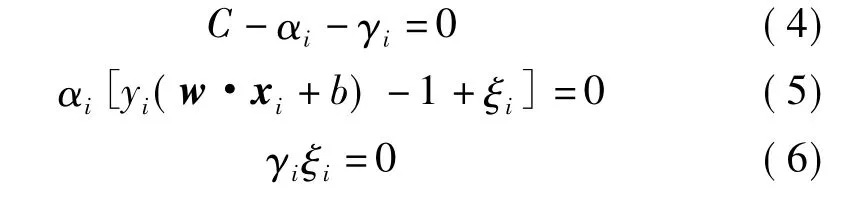
通过讨论SVM的部分KKT条件，以考察非线性可分情况下SVM的抗噪性。

文中所提的“管道壁”是指SVM中“最大间隔”的边缘，而“管道”是指最大间隔之间的部分。

(1)αi=0⇒γi=C⇒ξi=0，代入 yi(w·xi+b) －1+ξi＞0⇒yi(w·xi+b)＞1⇒样本位于“管道壁”外，为非支持向量。

(2)αi=C⇒γi=0⇒ξi＞0，代入 yi(w·xi+b) －1+ξi=0⇒yi(w·xi+b)=1－ξi＜1⇒样本位于“管道壁”里，为支持向量。

(3)0 ＜αi＜ =C⇒γi＞0⇒ξi=0，⇒yi(w·xi+b)=1⇒样本位于“管道壁”上，为支持向量。

从以上分析可见，当样本位于“管道壁”外及“管道壁”上时，ξi的值均为0，这时样本只会影响投影方向W。而当样本位于“管道壁”里时，ξi＞0，即这些样本决定SVM的目标函数的第二部分。当样本被正确分类时，0＜ξi＜1，否则 ξi＞1。当样本被正确分类但却含有噪声时，使本来应介于0和1之间的ξi变得＞1，显然会使目标函数值变大，背离了最小化目标函数的原则，不利于分类器改善。

讨论“管道”的宽度对SVM的影响。直观上讲，当“管道”越宽时，进入其中的样本数量越多，即支持向量个数越多。因为SVM服从聚类假设，当管道宽时，“管道壁”距离两类中心的距离越近，支持向量的个数就可能越多，这些支持向量中噪声的所占的比例就越低，即噪声对W的方向起到的作用就越少，这是其有利的方面;不利的方面是支持向量多了，原本对分类无影响的非支持向量的个数就减少，尤其当噪声数据由非支持向量变为支持向量时，可能减弱分类器的性能。

当“管道”越窄时，进入其中的样本数量就越少。原本是噪声的支持向量可能因“管道”变窄而成为非支持向量，对分类器不再产生影响，这是其有利方面;不利方面是“管道”越窄，距离两类中心的距离越远，样本数量越少，支持向量的个数也会相应少，这时若支持向量中有噪声，可能会大大影响W的方向，使分类器不再具有良好的判断能力。

综上所述，“管道”的宽窄各有利弊，研究的目标就是在“管道”宽度和进入管道的样本数量之间找到最佳值，即保证投影方向不会发生很大变化，又使错误率尽量降低。

2 实验结果

2.1 PubFig数据集

在PubFig数据集上随机选出的100个名人数据集上评估算法性能。PubFig数据集包含了200个公众人物的58797张图片，每个人有大量不同姿势、光照条件和表情的图片。图1(c)展示了一个人的所有图像［3］。PubFig分为一个60人的发展集和一个140人的估计集，见图1(a)和图1(b)。通常网站中给出的是图像的URL链接，经批量下载后得到图像，但由于网络等原因，所有的人脸不能全部下载成功，因此，实验中的图像是能够下载成功的部分。从所有图片中随机选取了100个不同的数据集进行实验。对于每个名人数据集，作为正类，其他随机选出的数量相同的图像作为负类，进行100次实验，取平均值作为最后结果。图2是一组类别噪声数据的举例，在没有噪声的数据中，正类为Bush的图像，负类为其他的人脸图像;含噪声的数据中，Bush图像中包含了其他的人脸图像，而其他人脸图像中也可能包含了Bush的图像。实验中对图像的处理采取以下方式:(1)定位图像中的人脸;(2)提取每张人脸的眼睛坐标;(3)将所有定位好的人脸图像根据眼睛坐标归一化，处理好的结果如图3所示，作为学习器的输入。

文中用到3个数据集:原始训练集、增量集与测试集，由随机划分的方式产生。对任一数据集而言，随机挑选30%的样本作为原始训练集、30%样本作为增量集，其余40%作为测试集。然后，根据一定的噪声率随机地将增量集中样本的类别标记取反，作为噪声。为模拟真实问题中噪声率的不同比例，分别采用了4种不同的噪声率，分别是10%，20%，30%和40%。在数据划分过程中，原始训练集、增量集和测试集中样本的分布保持一致［4］。为得到更加精确的结果，每种噪声都进行了20遍实验，将它们的均值作为最后的结果。值得注意的是，这个噪声率只与增量数据集相关，而与标记完全正确的原始数据无关。

2.2 实验结果

在实验中，所有的原始数据标签均正确，增量数据的标签随不同噪声率而有所不同。值得注意的两点:一是随着样本数目的增多，分类器的识别率会提高;二是随噪声率的不断增加，分类器识别率会降低。文中比较了以下方法:标准SVM，在其上训练的所有数据标签都是正确的，即没有任何噪声;增量数据分别含4种不同噪声率时的标准SVM;第3种方法是对前者的稍加改进，用原始数据来对增量数据赋一个置信度，根据置信度的高低来删除一部分被判定为噪声的数据，然后将删除后的数据与原始数据混合进行学习，分别尝试了删除10%～40%的数据后的学习方法。

图4和图5分别是原始数据识别率为67%时4种不同噪声率时PubFig数据集上Bush图像为正类的性能评估结果。以图4为例，介绍评估结果:SVM是指标号全部正确的SVM;noisy:10%withoutmissing是增量数据噪声率为10%时的标准SVM;noisy:10%with 10%missing是去掉10%数据后的方法;noisy:10%with 20%missing－noisy:10%with 40%missing是相应的去掉20%～40%数据后的改进方法。从中可见，噪声率较低时的SVM与标签全部正确时的标准SVM性能相当，证明了SVM具有抗噪能力。但由图4和图5可见，随噪声率的不断增加，这种抗噪能力越来越弱。对SVM进行适当的改进，即去掉一定比例的样本后，分类性能有了明显提高，比完全无噪声的标准SVM高几个百分点。

由上得出结论:在噪声率低于一定水平时，噪声对SVM没有太大影响，充分证明了SVM具备抗噪能力;且对SVM进行一定的改进，删除部分数据后，性能有了明显的提高，对噪声的鲁棒性也有所提高。

图4 噪声率为10%和20%时，去掉不同比率样本的结果

图5 噪声率为30%和40%时，去掉不同比率样本的结果

3 结束语

介绍了SVM并讨论了其抗噪性能。通过调节正则化参数，SVM可在最大化间隔和经验风险之间找到最佳值，在保证训练集错误率低的情况下提升了泛化能力。实验结果表明:在增量数据中含有噪声的情况下，SVM仍能够有效利用增量数据来提高学习器的性能并具备一定的抗噪能力。

改进的SVM方法失去了一定比例的训练样本，提高了整个数据集的质量，学习器的最终性能也可能有所改善。但如前面所述，这种方法性能好的前提是原始数据集的质量要好，能否放宽对原始数据的限制，使分类器在不受约束的条件下改进性能是进一步研究的重点。

［1］邓乃扬，田英杰.支持向量机 －理论、算法与拓展［M］.北京:科学出版社，2009.

［2］ZHU X，WU X，CHEN S.Eliminating class noise in large datasets［C］.Washington D.C:Proceedings of the 20th ICML International Conference on Machine Learning，2003:920 －927.

［3］NEERAJ K，ALEXANDER C B，PETER N B，et al.Describable visual attributes for face verification and image search［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33(10):1962 －1977.

［4］THEODOROS E，MASSIMILIANO P，TOMASO P.Statistical learning theory ［J］.International Journal of Computer Vision，1998，38(1):9 －13.

［5］候雪梅.一种SVM多类分类算法用于抗噪语音识别［J］.西安邮电学院学报，2009，5(5):106 －108，141.

［6］吕卓，谢松云，赵金，等.基于SVM及其改进算法的fMRI图像分类性能研究［J］.电子设计工程，2011，19(16):30－33.