干涉基线对地震形变场的影响——以玛尼地震同震-震后形变场为例

屈春燕 单新建 张国宏 宋小刚 张桂芳 刘云华 郭利民

(中国地震局地质研究所，地震动力学国家重点实验室，北京 100029)

0 引言

作为一种新型的空间对地观测技术，D-InSAR对地表形变具有很高的敏感度，可用于测量cm级甚至mm级的地表相对形变量。这为地震同震-震后形变场乃至震间微小地壳形变场的观测提供了前所未有的新途径。这一点已被国内外多个震例的研究结果所证实(Massonnet et al.，1994;单新建等，2004;Michael et al.，2006;Wang et al.，2007;Shan et al.，2007;许才军等，2008)。不过目前该技术尽管在理论上很完善，但在实际应用和数据处理过程中仍有许多不确定因素和技术问题需要深入研究和解决。这主要是由于D-InSAR形变观测受许多因素的影响，而干涉基线是众多影响因素中最为重要和关键的一个。一方面干涉基线的大小对像对的相干性起决定性作用，限制着有效干涉对的数量和干涉测量的可行性;另一方面干涉基线估计的准确性又直接影响形变观测结果的精度和可靠性(孟祥东等，2008;何平等，2009)。因为在干涉相位的差分处理过程中，参考椭球面相位(平地相位)和地形模拟相位的计算与去除都需要根据干涉基线进行。如果干涉基线不能被准确地估计，就会造成平地相位残留和地形相位的残留，而这些残留的相位成分将被误认为形变分量，这就势必降低形变测量结果的可靠性。因此，研究干涉基线对地震形变场探测的影响，探索最优基线估计方法是非常重要且必要的工作。

1997年西藏玛尼7.9级地震是D-InSAR干涉测量技术应用于地震形变场探测的典型成功案例。由于玛尼震区气候干燥，地表裸露，地形相对平坦，去相干因素少，因而雷达数据的相干性保持得很好。自1997年玛尼地震发生以来，国内外不少学者利用D-InSAR技术研究和提取了玛尼地震的同震干涉形变场，但综合分析前人的研究成果不难发现，不同学者得出的断层两盘相对LOS向位移有明显差异(单新建等，2004;Wang et al.，2007;Shan et al.，2007;许才军等，2008)。这与不同学者所用的SAR数据源、处理软件及处理方法等的不同有关，但也可能与干涉基线的估计方法及相位误差的去除程度不同有关。比如基于SAR图像本身携带的粗略轨道数据进行基线估计所得到的结果与基于DEOS精密轨道数据进行基线估计得到的结果就会有明显差异。前者会造成较大的轨道和地形残留相位，致使差分条纹密集而观测结果偏大。为此，本文以玛尼地震同震-震后的ERS2干涉数据为例，对比分析了基于粗略轨道数据、精密轨道数据、干涉条纹频率及地面控制点等多种基线估计方法及其对同震-震后形变场观测结果的影响，这对完善InSAR技术在地震形变场探测中的应用具有重要意义。

1 干涉基线及其估计方法

1.1 干涉基线对参考相位和地形相位的影响

干涉基线定义为两副天线的空间或时间的矢量几何关系，是InSAR观测中一个非常重要且关键的参数(郑芳等，2005;孟祥东等，2008;何平等，2009)。其重要性就在于:一方面，基线和2次SAR成像的斜距构成一个三角形，使2次观测生成的图像对之间具有了相干性，使干涉测量得以进行;另一方面，基线又是导致图像对相干性降低的重要根源，基线越大，两幅图像之间的相干性越弱。同时，基线也是影响形变测量精度的主要因素。因为轨道(参考面)相位和地形相位的计算与去除都直接依赖于干涉基线，若基线估计不准确，造成的轨道残留相位和地形残留相位就会混入形变相位中，从而降低形变观测结果的精度和可靠性。

图1所示为重轨InSAR干涉观测的原理示意图(何平等，2009)。图中S1，S2为卫星2次观测的天线中心位置，ρ1为S1到地面点P的距离，ρ2为S2到地面点P′的距离，D为P到P′的距离，P0为点P在参考表面上的投影点，he为P0到P点的距离，θ为S1的视角，B为基线长度，α为基线B在水平方向的夹角，θ0为P0的视角，δθ=θ-θ0，Δρ为视距地表形变量。在忽略大气相位和噪声相位的理想情况下，从2幅配准后的SAR图像经干涉处理得到的初始干涉相位由3部分组成，用公式表示为

式(1)中φref为参考椭球面引起的相位贡献量(参考相位);φtopo为参考面以上地形起伏产生的相位贡献量(地形相位);φdef为地表形变相位，若无形变，则该项为零。根据干涉观测原理，上式中右3项可表达为下列关系式(孟祥东等，2008):

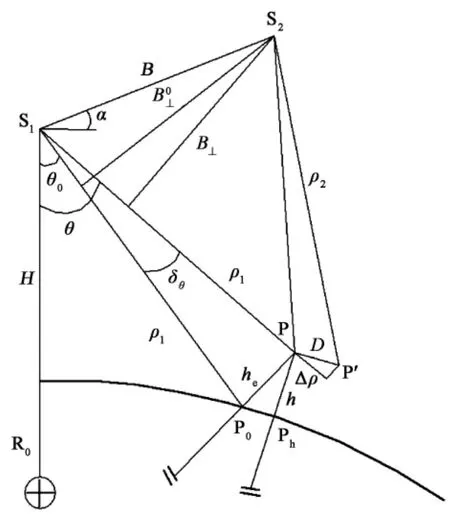
图1 干涉测量及干涉基线几何示意图(何平等，2009)Fig.1 Sketch map for principle of SAR interferometric measurement(after HE Ping et al.，2009).

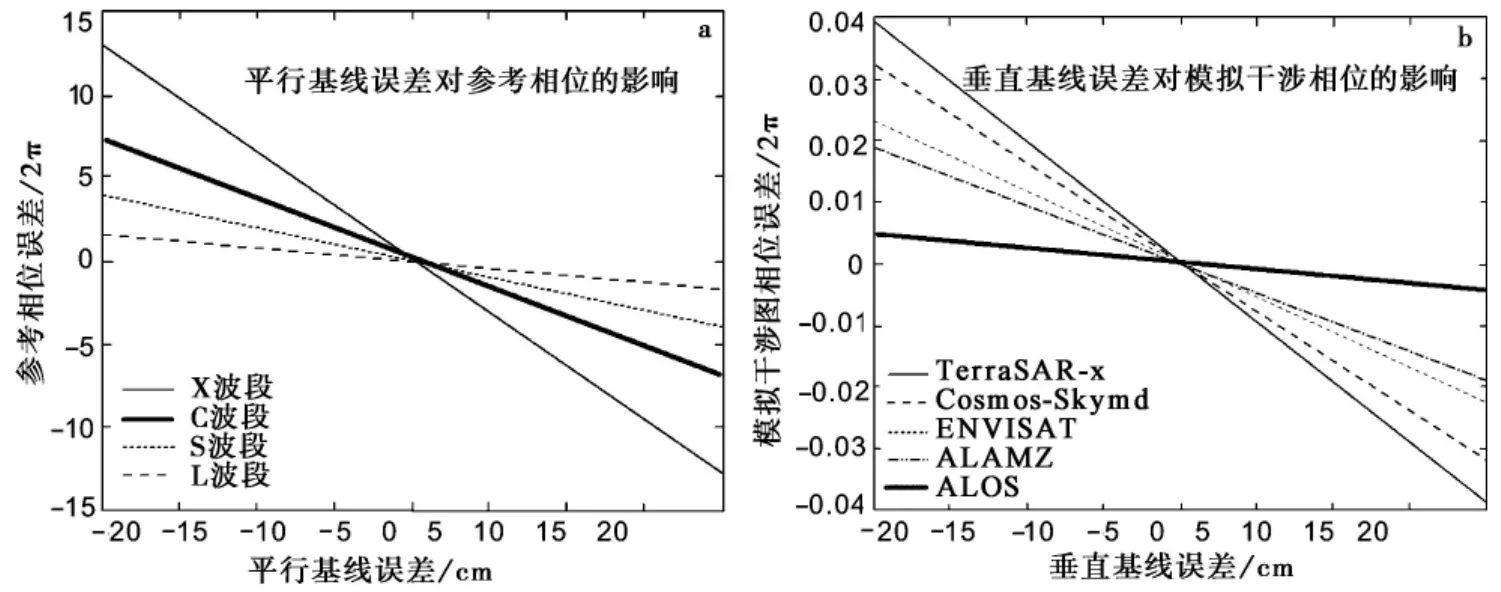
图2 不同波段卫星的参考相位误差及模拟地形相位误差与干涉基线误差的关系(何平等，2009)Fig.2 Relation between phase errors and interferometric baseline for SAR data with different wave bands(after HE Ping et al.，2009).

1.2 干涉基线的估计方法

为了获得更好的基线估计，GAMMA等常用干涉SAR处理软件均提供了多种基线估计的算法，这些算法包括从轨道状态矢量估计基线，从SLC的配准偏移量估计基线，从干涉相位本身(干涉条纹频率)来估计基线，从地面控制点利用最小二乘法估计基线等。实际应用表明，这些方法中有的对平行基线的估计效果好，有的对垂直基线的估计效果好，而将这些方法的2种或多种联合使用往往能获得最佳基线估计。

1.2.1 基于粗/精轨道状态数据的基线估计

卫星轨道状态数据是指成像瞬间卫星的位置坐标(XS，YS，ZS)和速度矢量(VX，VY，VZ)。一般说来，ERS-1/2和ENVISAT的影像头文件中都附带了5个时刻的粗略轨道状态数据，其综合精度在1m左右。据此可以进行干涉基线估计。另外，国际上有些机构如ESOC(European Space Operations Centre)、DEOS(Delft Institute for Earth-Oriented Space Research)和 DORIS(Delft Object-orien-ted Radar Interferometric Software)等从事ERS-1/2和ENVISAT卫星的定轨服务，可以提供更多个成像时刻的精密轨道状态数据。但由于所采用的计算模型和定轨方案等的差异，不同机构算得的轨道参数精度是不一样的。据相关研究和分析，荷兰Delft大学DEOS提供的精密轨道数据精度较高，轨道径向精度达到5～6cm，法向精度优于20cm。根据精密轨道状态数据可得到更为精确的干涉基线估计。

1.2.2 基于干涉相位的基线估计

通过对干涉相位做距离向傅里叶变换(FFT)，计算干涉相位变化的瞬时频率，利用2个距离向位置对应的瞬时频率联立方程来计算垂直基线和平行基线(孟祥东等，2008;何平等，2009)。这种方法对垂直基线的估计精度优于平行基线，尤其在地形平坦的地方可以获得精确的垂直基线估计。但在干涉相位噪声较大以及观测区域山地覆盖面积较大等非理想情况下，基线估计精度会明显下降。因此，一般选择图像中比较平坦的区域进行FFT基线估计，而且FFT变换的窗口大小也要根据地形起伏情况适当调整。一个较大的FFT变换窗口往往会降低垂直基线的估计精度。在缺乏轨道状态数据或轨道状态数据质量较差时，这种基于干涉相位傅里叶变换的基线估计方法显得尤为重要。另外，利用这种方法消除去平地效应后的干涉纹图中残留的轨道相位误差也是很有效的。

1.2.3 基于地面控制点的最小二乘基线估计

通过基于地面控制点的最小二乘基线估计方法对初始基线进行优化和精校正，进而获得高精度的基线估计值。这种方法需要选取至少20个地面控制点的高程，这些地面控制点可以从地形图或DEM上获取，也可以是GPS的实测值。人工角反射器可作为理想的地面控制点。控制点应在图像上均匀分布，而且要尽量分布于不同高程的平坦区域上。

2 玛尼地震概况及干涉数据处理方法

2.1 玛尼地震概况

1997年11月8日，在西藏自治区那曲地区玛尼乡发生了MS7.9地震，称为玛尼地震。震中位于35.2°N，87.3°E。玛尼地震发生在藏北高原北部长达270km的玛尔盖茶卡断层附近(徐锡伟等，2000;单新建等，2004)。野外考察资料表明(徐锡伟等，2000)，玛尼地震的地表同震破裂带长120km，以左旋剪切为主，最大左旋位移量达4.5m，其东西两侧水平位移为2～3m，最大地裂缝带宽度为300～400m。基于地震波形资料的震源参数反演结果也表明，断层性质为左旋-逆走滑断层，破裂方式为由西向东(许力生，1999)。玛尼地区气候干燥，地表裸露，地形相对平坦，去相干因素少，SAR图像的相干性高，是开展InSAR干涉形变场观测研究的理想场地和理想数据源。因此，本文以玛尼地震同震和震后干涉数据为例来讨论干涉基线对地震形变场的影响。

2.2 干涉数据选取及处理

对于同震形变场观测，应尽量选择垂直基线小的干涉对，这样既能保证高质量的相干性，又能弱化地形相位的影响。同时，震前-震后的时间间隔也要尽可能的短，以减少震后弹性回跳形变的混入及余震的影响。而对于震后形变场的观测，成像时间间隔要适当延长。据此我们选择了覆盖玛尼震区的6景ERS2雷达数据，数据模式为vv极化、IS2成像模式的降轨数据。震前2景，震后4景，构成2个同震干涉对和4个震后干涉对。各干涉对的雷达数据参数如表1所示，数据覆盖范围如图3a所示。从表1可以看出，各干涉对的垂直基线都很小，最大的也只有150m，而相应模糊高则比较大，这可以有效抑制地形残余相位的影响。

表1 选用的ERS－2雷达数据参数Table 1 ERS-2 radar data parameters selected

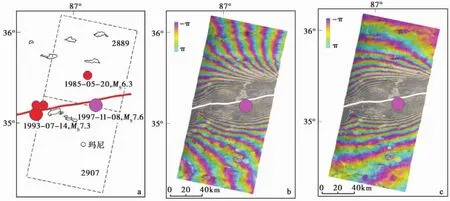
图3 不同基线条件下的同震干涉纹图Fig.3 The coseismic interferograms with different baseline corrections.

对于选定的干涉数据对，我们采用2-pass+外部DEM的干涉处理算法，以GAMMA软件为处理平台。采用美国宇航局发布的空间分辨率为3弧秒的SRTM DEM去除干涉相位中的地形相位分量。SRTM DEM数据标称的绝对高程误差＜16m(单新建等，2004)。本文所使用干涉像对的最大空间垂直基线为150m，按照相应的模糊高换算，理论上由DEM误差引入的相位误差约7.6mm，相当于1/4个干涉条纹周期。实际上3弧秒空间分辨率的SRTM DEM数据在地形平坦区域的精度要高于地形起伏的山区，在平原区其绝对高程误差＜5m。而位于藏北高原上的玛尼震区地形起伏不大，相对高差小，按照5m的高程精度换算，由DEM误差引入的相位误差仅为2.4mm，相当于1/12个干涉条纹周期。这样小的量级对于数十cm的同震形变场是没有什么影响的，对于数cm量级的震后形变场也是可以忽略不计的。

另一方面，大气相位影响也不是玛尼震区的主要误差源。Zebker等(1994)的试验研究表明，在空间垂直基线为100～400m的条件下，大气状况发生20%的相对湿度变化，将导致10～14cm的形变误差。而对于气候干燥、地表裸露的玛尼震区，大气湿度相对变化很小，大气相位误差也应很小。小量级的大气相位通过多视处理和空间滤波已基本去除。即使有明显的残余大气相位，也可以通过同一地区不同干涉对的对比及其残余相位的空间分布位置和形态加以识别和去除。因为大气相位变化具有高度的时间不相关性，其在不同干涉对上的出现是不同的。其次，大气相位变化独立于活动构造，大气引起的干涉条纹是区域状分布的，而地震引起的形变条纹总是围绕发震断层展布。根据这些我们可以判断和去除大气相位。

本文分析认为，干涉基线误差导致的轨道残留相位是地震形变场观测的主要误差因素，而且难以识别，因为轨道因素影响每个像元，轨道残留相位与形变相位复合使差分条纹密集，很容易被误认为形变条纹，从而导致形变观测结果的整体性偏差。因此，本文处理过程中着重探索干涉基线误差对玛尼地震同震和震后形变场的影响，对比分析基于粗略轨道数据、精密轨道数据、干涉条纹频率及地面控制点等多种不同基线估计条件下的干涉形变场图像特征。相位解缠采用MCF最小费用流解缠算法，先对高质量的区域进行解缠，得到可靠的解缠相位值，然后以这些可靠相位值为模型，通过插值实现对其他低相干区域的解缠。在解缠前对缠绕差分相位进行了多次窗口逐渐减小的自适应滤波以改善相位解缠质量。最后处理得到的结果如图3～7所示。

3 不同基线估计的玛尼地震同震干涉形变场

3.1 粗/精轨道数据估计的同震形变干涉纹图

图3为处理得到的玛尼地震同震形变干涉纹图。其中，图3a为SAR图像覆盖范围和研究区构造背景。图3b为基于粗轨数据估计基线的处理结果，3c为基于精轨数据估计基线的处理结果。图3b中，在断层附近干涉条纹沿断层走向呈包络线状分布，条纹很密集。在断层两侧40～50km以外的区域，干涉条纹密度降低，条纹走势逐渐偏离断层走向，形成斜交于发震断层的扇形条纹，而且是断层上盘干涉条纹向西突出，下盘向东突出，形成类似左旋扭动的态势。图3c中，不论是断层附近还是断层远场区域，干涉条纹都沿发震断层走向呈包络线状分布，只是越靠近断层条纹越密集，越远离断层，条纹越稀疏，而且衰减得比较快，看不出明显的左旋运动态势。很明显图3c较真实地揭示了玛尼地震的同震形变场，而图3b中则含有较多的轨道残余条纹，在断层附近由于地震引起的形变相位占主导地位，因此二者复合后形成的条纹仍然呈包络发震断层的形态分布，而在远离断层的上下盘远场区，由于地震引起的形变相位减少，二者复合后便形成斜交于发震断层的扇形条纹。条纹显示的左旋扭动态势并非意味着发震断层的左旋走滑运动。实际上，形变干涉条纹只能定性反映形变场的整体分布范围和形变梯度的变化趋势，而断层两盘的相对形变方向和具体形变量要通过相位解缠后的数值化干涉位移场才能确定。可见，在进行地震形变场提取时必须进行精轨数据的基线矫正，否则残留的轨道相位会使观测结果明显偏大，甚至引起错误解释。

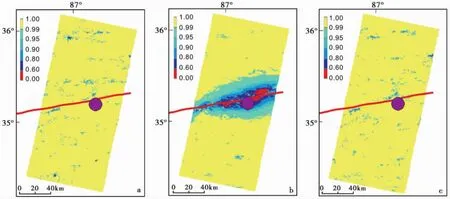
图4 玛尼地震震前、同震和震后相干图Fig.4 The pre-seismic(a)，co-seismic(b)，and post-seismic(c)coherence maps of Mani earthquake.

图5 精密轨道校正后的同震干涉位移(白色虚线示剖面位置)Fig.5 Co-seismic interferometric displacement after correction of fine orbit state vectors.

从图3c也可以看出，玛尼地震同震形变场主要集中于距断层40～50km的近场区域，在这一区域以外形变衰减得很快。这正与图4显示的结果相一致。图4所示为玛尼地震震前、同震和震后的相干图。可以看出震前、震后相干性都很好，而在同震相干图上沿发震断层走向出现了显著的低相干区域，而且是围绕发震断层条带状分布。与图3c所示的同震干涉纹图对比，可以发现这个低相干带正反映了同震形变场波及的主要区域。可见相干图也包含了丰富的形变信息，根据相干图可以分析判断地震形变场的影响范围和主破裂带的空间位置。

3.2 精轨基线校正后的干涉位移场

图5所示为对精轨校正后的干涉纹图(图3 c)进行相位解缠得到的数值化干涉位移场。图5表明，玛尼地震造成的同震形变主要集中在断层两侧距离断层40～50km的条带状区域内，此区域以外随着断层两侧距离的增加，形变梯度大幅下降，形变衰减较快。在断层北盘LOS向位移为负值，表示形变方向为沉降或向西运动。在断层南盘LOS向位移为正值，表示形变方向为隆升或向东运动。由于震后野外考察、震源机制解及基于波形资料的震源参数反演结果都一致表明玛尼地震的断层运动性质为左旋走滑，因此，可以判断断层北盘和南盘分别向西和向东运动，反映的也正是左旋走滑运动方向，与野外考察等其他结果一致。

由于LOS位移反映的是每个像元所在位置沿斜距向的位移(卫星到地面观测单元之间距离的变化)，是真实地表位移在斜距方向上的投影，而野外考察得到是断层两侧的相对位错量。二者缺乏直接可比性。为此，我们将LOS向位移分别折算成垂直位移和沿断层走向的水平位移，3种位移分别如图5 a，b，c所示。为了更清楚地揭示断层两侧的相对位移大小和位移梯度衰减情况，我们构建了1条跨断层位移剖面，剖面位置如图5中的白色虚线所示，剖面上的位移曲线如图6所示。综合图5和图6，可以看出垂直位移与LOS向位移的大小接近，其在断层两盘的最大相对变化量达2.0m。而沿断层走向的水平位移要明显大于LOS向位移，其在断层南北两盘的最大相对位移约4.5m。这正与野外考察结果相一致。图6中沿断层所在位置的灰色网状条表示紧邻断层两侧干涉条纹紊乱不连续的区域，这一区域的位移是插值解缠的结果，可能不可靠。

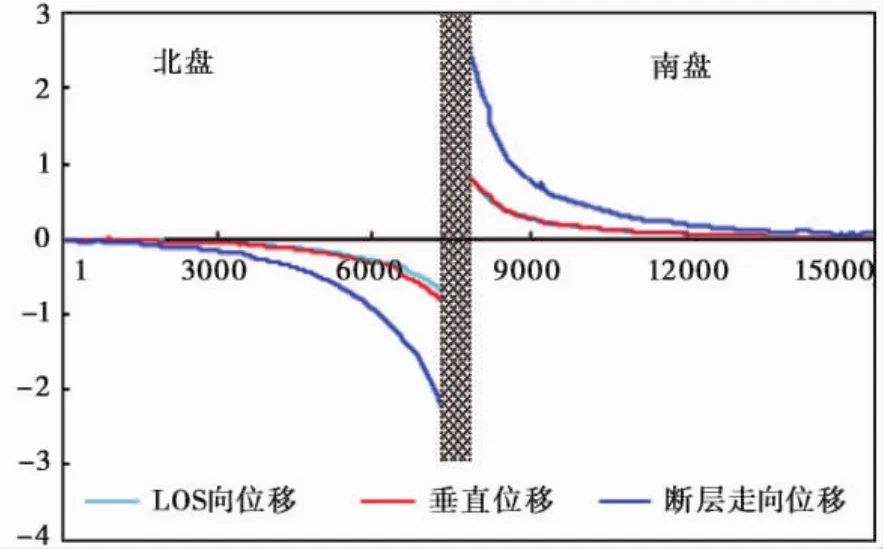
图6 跨断层同震干涉位移剖面图Fig.6 The profile of co-seismic displacement across fault.

4 不同基线估计的玛尼地震震后干涉形变场

为反映震后形变的缓慢变化过程，选择了震后不同时间间隔的2个干涉对，一个是19971202-19990406，从震后24d到震后508d，时间跨度为484d。以下简称震后干涉对1。另一个是19980421-19990406，从震后163d到震后508d，时间跨度为345d。以下简称震后干涉对2。由于震后形变远小于同震形变，因此，需采用更为严格的误差控制措施。为考察不同基线估计方法对震后形变场的影响，我们首先对2个震后干涉对进行基于粗/精轨道数据的基线估计与差分处理，得到的结果如图7 a，7b和7d，7e所示。其中，图7a，7b表示震后干涉对1，图7d，7e表示震后干涉对2。很显然基于粗轨数据基线估计得到的差分干涉纹图(图7 a，7d)中含有大量轨道残留相位，在断层附近由于形变相位的作用使差分干涉条纹发生了左旋弯曲，而在断层两盘震后形变量很小甚至没有，主要是轨道残留条纹。基于精轨数据基线估计的结果(图7 b，e)，虽然差分条纹有所减少，但仍具有明显的线性趋势，说明相对于数cm量级的震后微小形变，基线误差引起的轨道残留相位依然是显著的，还需进一步提高基线估计的精度。为此，我们利用GAMMA软件提供的算法，进行了基于干涉条纹频率的基线矫正和基于地面控制点的基线优化，以去除多余的趋势性条纹，得到的结果如图7 c，f所示。

图7 不同基线条件下的震后形变干涉纹图Fig.7 Post-seismic interferograms with different baseline corrections.

从图7c上可以明显看出有2条NE的干涉条纹，其分布位置正好与发震断层走向一致，而且紧靠发震断层。因此，我们认为这是震后形变场的反映。每个条纹表示2.8cm的LOS形变量，2个条纹代表5.6cm的形变量。在断层的上下盘有片状色块，分析认为这可能是局部大气影响，而不是地震形变，而且它也不影响对地震形变场的判断。从图7f上可以明显看出有1条沿断层走向分布的NE干涉条纹，我们认为这是震后形变的反映，它代表2.8cm的LOS形变量。综合分析2个不同时间跨度的震后形变观测结果(图7 c，7f)，可以看出玛尼地震的震后形变特征是:1)震后形变场的影响范围很小，集中在断层沿线10～20km宽的长条区域内;2)震后形变方向与同震形变方向相同，仍然显示左旋运动趋势;3)从震后24d至508d的形变量达到5.6cm，而从震后163d至508d的形变量约2.8cm。说明震后形变在数cm的量级上，而且随着时间推移，形变幅度逐渐减小。

5 讨论与结论

(1)作为一种新型的空间对地观测技术，D-InSAR对地表形变具有很高的敏感度，可进行cm级甚至mm级的相对形变测量。这对地震同震-震后形变场乃至震间微小地壳形变场的观测都是很有意义的。但D-InSAR形变测量的误差因素很复杂，理论上，任何使2次重轨观测的雷达波产生相位延迟的因素，如卫星轨道状态、地形起伏、大气非均匀变化，地物介电常数变化等都对干涉相位有一定贡献。要准确提取地震引起的地表形变相位，需扣除其他所有因素的相位贡献量。实际应用中通常考虑的是轨道相位、地形相位和大气相位这3种误差源。由于这些误差与所用数据的垂直基线、观测环境地形起伏状况、地表覆盖类型及大气变化等密切相关，因而具有很大的随机性。目前尚缺乏有效、公认和通用的误差去除方法，需要研究者根据实际数据处理情况结合经验来判断和去除。这就导致了研究结果的差异性和精度的不确定性。尤其在测量震后及震间微小形变时显得尤为突出。因此，如何建立有效的误差去除与控制机制，提高干涉形变观测的精度和可靠性是InSAR技术进一步发展要突破和解决的关键问题之一。

(2)选取合适的数据集和处理方法，InSAR技术能够提供直观、定量高精度的同震形变及震后形变信息。本文以ERS2 SAR图像为数据源，以1997年11月8日的西藏玛尼地震为例，对比分析了不同基线估计条件下的同震-震后形变场，探讨了干涉基线对地震形变观测的影响。结果显示，基于ERS2 SAR图像本身携带的粗略轨道状态数据估计基线会造成较多的轨道残留相位，致使差分干涉条纹密集且形态发生扭转，易导致对形变场的错误解释。因此，必须利用精密轨道数据进行干涉基线估计。有时还需要进行基于干涉条纹频率的基线矫正，以去除多余的趋势性相位。但这种方法并非普遍适用，需根据干涉条纹形态及其与断层的关系，并结合经验来判断。过度去除会造成形变相位的损失。本文处理得出的玛尼地震同震形变场沿断层走向的南北盘最大相对左旋位移约4.5m，与野外调查的结果一致。得出的震后形变场主要集中在断层附近10～20km的狭长条形区域内，震后508d的累积形变量至少达5.6cm，随着时间延续，震后累积形变量增加。如能获取到更多的震后时序干涉数据，则可以研究震后形变场的时间演化过程。

何平，许才军.2009.卫星轨道误差对SAR干涉处理的影响研究［J］.大地测量与地球动力学，29(5):54—57.

HE Ping，XU Cai-jun.2009.Research on effect of satellite orbit error on SAR Interferometry［J］.Journal of Geodesy and Geodynamic，29(5):54—57(in Chinese).

孟祥东，王彤，保铮.2008.干涉合成孔径雷达的垂直基线对图像相干性的影响［J］.电子学报，36(6):1222—1226.

MENG Xiang-dong，WANG Tong，BAO Zheng.2008.The effect of the perpendicular baseline on coherence for SAR images in InSAR ［J］.Acta Electronica Sinica，36(6):1222—1226(in Chinese).

单新建，马瑾，王长林，等.2004.利用D-InSAR技术获取的地表形变场提取玛尼地震震源断层参数［J］.中国科学，32(11):837—844.

SHAN Xin-jian，MA Jin，WANG Chang-lin，et al.2004.Co-seismic ground deformation and source parameters of Mani M7.9 earthquake inferred from spaceborne D-InSAR observation data ［J］.Science in China(Ser D)，47(6):481—488.

唐晓青，向茂生，吴一戎.2008.一种改进的基于干涉相位的基线估计方法［J］.电子与信息学报，30(12):2795—2799.

TANG Xiao-qing，XIANG Mao-sheng，WU Yi-rong.2008.An improved baseline estimation approach based on the interferometric phases［J］.Journal of Electronics＆ Information Technology，30(12):2795—2799(in Chinese).

许才军，温扬茂.2008.基于InSAR数据的西藏玛尼MS7.9地震的地壳不均匀性研究［J］.武汉大学学报，33(8):847—849.

XU Cai-jun，WEN Yang-mao.2008.Nonhomogeneity of the crust from MS7.9 Manyi(Tibet)earthquake with InSAR observation［J］.Geomatics and Infomation Science of Wuhan University，33(8):847—849(in Chinese).

许力生，陈运泰.1999.1997年中国西藏玛尼MS7.9地震的时空破裂过程［J］.地震学报，21(5):449—459.

XU Li-sheng，CHEN Yun-tai.1999.Temporal-spatial rupture process of 1997 Mani，Tibet earthquake［J］.Acta Seismological Sinica，21(5):449—459(in Chinese).

徐锡伟.2000.中国地震年鉴:藏北玛尼地震科学考察［M］.北京:地震出版社.

XU Xi-wei.2000.Yearbook of China Earthquake Research:Scientific Investigation of Mani Earthquake in North Tibet［M］.Seismological Press，Beijing(in Chinese).

郑芳，马德宝，裴怀宁.2005.干涉合成孔径雷达基线估计要素分析［J］.遥感信息，(3):7—10.

ZHENG Fang，MA De-bao，PEI Huai-ning.2005.Analysis of the elements of baseline estimation of interferometric SAR［J］.Remote Sensing Information，(3):7—10(in Chinese).

Massonnet D，Feigl K L，Rossi M，et al.1994.Radar interferometric mapping of deformation in the year after the Landers earthquake［J］.Nature，369:227—230.

Michael Taylor，Gilles Peltzer.2006.Current slip rates on conjugate strike-slip faults in central Tibet using synthetic aperture radar interferometry［J］.Journal of Geophysical Research，111，B12402.doi:10.1029/2005JB00401.

Shan X J，Zhang G H.2007.A characteristic analysis of dynamic evolution of preseismic-coseismic-postseismic inerferometric deformation fields associated with the M7.9 earthquake of Mani，Tibet in 1997 ［J］.Acta Geological Sinica(English Edition)，81(4):587—592.

Wang H，Xu C J，Ge L L.2007.Coseismic deformation and slip distribution of the 1997 MW7.5 Manyi，Tibet，earthquake from InSAR measurements［J］.Journal of Geodynamics，44(2007):200—212.

Zebker H A，Rosen P A，Goldstein R M，et al.1994.On the Derivation of Coseismic Displacement Fields Using Differential Radar Interferometry:The Larders Earthquake［J］.J Geophys Res，99(B10):19617—19634.