刚性壁面三维陷落腔涡流噪声机理研究

王 玉，王树新，刘玉红

（天津大学 机械工程学院，天津 300072）

刚性壁面三维陷落腔涡流噪声机理研究

王 玉，王树新，刘玉红

（天津大学 机械工程学院，天津 300072）

陷落腔结构作为船舶表面的一种常见结构，其产生的噪声近年来广受关注。文章在马赫数为0.004 8条件下，采用LES-Lghthill等效声源法对刚性壁面三维陷落腔的流场及声场进行仿真，形象地再现了陷落腔内部涡旋运动变化规律，分析了陷落腔涡流流动机制、脉动压力特性以及辐射噪声特征。通过对脉动压力功率谱及声功率频谱的对比分析发现，声功率谱的前三阶频率与陷落腔流体动力振荡频率吻合，这表明刚性壁面的三维陷落腔涡流噪声由流体动力振荡引起，由脉动压力构成的偶极子源对涡流噪声的贡献最大。研究成果为控制船舶涡流噪声提供了理论依据。

三维陷落腔；涡流噪声；大涡数值模拟；等效声源法；涡声关系

1 引 言

陷落腔作为船舶表面的常见结构，其产生的涡流噪声对搭载在船舶上的声学传感器有不容忽视的影响，不仅会增加声学测量仪器的背景噪声，还会对外界声信号的测试产生干扰。随着现代科技的迅速发展，船舶结构日益复杂，航速日趋提高，航速的提高势必增大了涡流噪声，因此，对船舶陷落腔结构涡流噪声的研究具有重要意义[1-4]。

陷落腔流动噪声涉及流体、噪声以及结构之间的相互耦合，给理论分析、试验研究以及数值模拟都带来很多困难。近年来，许多学者在该领域开展了相关研究并取得了一定成果。Fuglsang和Cain[5]采用Baldwin-Cain湍流模式和直接数值模拟相结合的方法考察空腔流动，重点研究强迫剪切层作用。Rossiter[6]给出了辨识孔腔流动模态振荡共振频率的公式。Guiliaume等人[7]采用数值方法对三维可压缩陷落腔的不稳定流动进行了研究，发现一阶振荡频率比Rossiter的二维结果要低。Ask等人[8]计算了马赫数为0.15、长深比为4的二维长方形孔腔的绕流问题，得到了壁面脉动压力是重要的偶极子声源。Larsson等人[9]研究了低马赫数层流条件下二维空腔的气动噪声，考察了各种声源项在辐射声能中所占的比重，结果表明由面积分项即由壁面压力脉动引起的偶极子辐射占绝对优势。耿冬寒和王玉[10]采用混合LES-FW-H声类比方法研究了浅腔的流动噪声。

本文采用大涡数值模拟 （LES）－Lighthill等效声源法对船舶三维陷落腔产生的涡流噪声进行仿真，首先采用LES方法求解陷落腔非定常流场，得到其流体动力声源。在此基础上，采用Lighthill等效声源法计算陷落腔噪声源及远场涡流噪声辐射。通过分析陷落腔流动机制、脉动压力特性以及辐射噪声特征，阐述了陷落腔涡流噪声与涡流动力振荡的相关性。

2 有限元模型

2.1 几何模型

本文研究的三维陷落腔，其长深比L/D=2:1，长宽比L/W=1.5:1。

2.2 流场模型

计算区域高度方向Y/D=5；沿流动方向，上游长度L1/D=4，下游长度L2/D=8；沿延展方向，Z/D=4。整个流场区域采用非均匀结构化网格，空腔外部计算区域分为9个子区域，空腔靠近边界处网格较密集，随边界距离的增加网格逐渐稀疏，经网格独立性检验后网格总数约为1 500 000，壁面y+≈3。由于实际网格较密集，图1示出了流向网格的不均匀分布。

陷落腔进口来流速度为7 m/s，流体介质为水，马赫数Ma=0.004 8，基于陷落腔深度的雷诺数ReD=1.05×106。为了模拟实际湍流，在进口给定5%的随机扰动。壁面设置为无滑移恒温不渗透固体边界；陷落腔外法向及展向边界为对称边界，速度与压力梯度均为零；出口边界条件按照不可压缩流动条件满足质量守恒。几何模型及边界条件如图2所示。

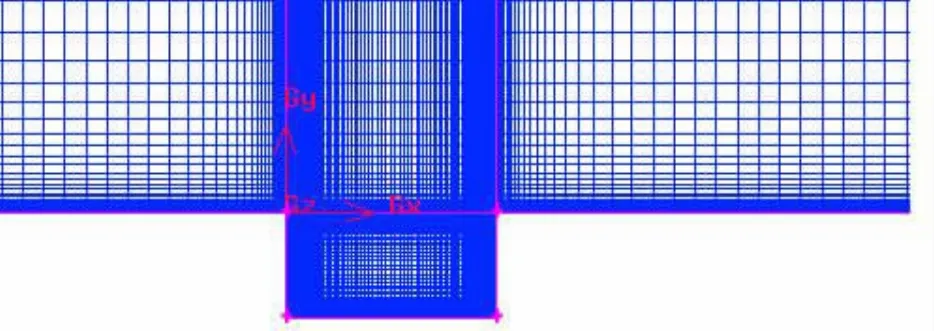
图1 陷落腔流向网格划分示意图Fig.1 Meshing schematic of cavity in streamwise direction

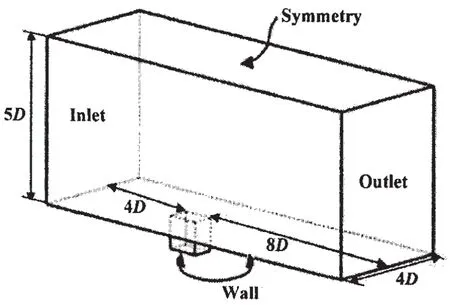
图2 陷落腔几何模型及流场边界条件示意图Fig.2 Schematic configuration and computational domain of the cavity

2.3 声场模型

基于有限元/无限元法建立声场模型，有限元区域用于预测噪声近场传播，无限元区域用于预测噪声远场传播，如图3所示。其中声源区网格比较密集，有限元区网格划分满足s＜λ/6，s为网格尺寸，λ为一定频率下的波长。经网格独立性测试，声源区最大网格1 cm，整个有限元区域最大网格尺寸为2.4 cm。无限元二维网格确保与有限元三维网格匹配，无限元设为无反射边界条件。

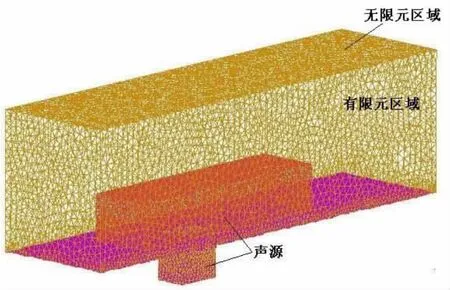
图3 陷落腔声场模型及边界条件示意图Fig.3 Cavity model and boundary conditions in the sound field

3 计算方法与求解

本文选用LES-Lighthill等效声源法对三维陷落腔的流场及声场进行求解，关于该方法的可靠性与准确性在文献[11-12]已有详细阐述，在此不再赘述。为了使非定常流场求解易于收敛，首先采用标准k-ε模型进行定常求解，以此解作为非定常计算的初始条件，采用LES方法模拟涡旋产生、发展和耗散的变化过程。然后采用Lighthill等效声源法计算声场信息。关于时间步长的选取，满足流场同声场求解统一，确定时间步长为1×10-5s。

3.1 流场求解

本文采用LES方法对流场进行求解。LES是介于直接数值模拟（DNS）和雷诺应力模拟（RSM）之间的湍流数值模拟方法。该方法通过滤波函数，将大尺度的湍流运动直接计算出来，而小尺度涡对大尺度涡运动的影响则采用引入附加应力项进行修正。其基本控制方程为通过滤波函数处理的瞬时状态下Navier-Stokes方程及连续方程：

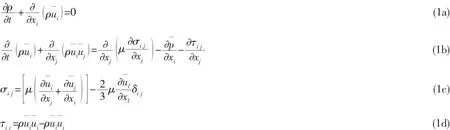
式中：μ为水的动力粘度，ui表示各个坐标维度的平均速度，σij为分子粘性引起的应力张量，τij为亚格子应力。

亚格子应力是由滤波运算得到的未知量，需要采用模型予以封闭，进而衡量亚格子尺度的湍流应力。为使计算更加精确，选用动态Smagorinsky-Lilly[13]模型模拟亚格子湍流应力尺度效应，该方法基于已求解的流动信息动态计算涡粘模型的系数。亚格子尺度湍流应力的具体形式如下：

3.2 声场求解

采用Lighthill等效声源法对声场进行求解。该方法最早由Lighthill[14]提出用于计算自由空间条件下的气动声学问题，并未涉及固体边界以及运动物体对气动噪声的影响。本文在不可压缩流体流动条件下，研究对象为具有固体边界的陷落腔模型，因此，采用Lighthill声类比方程的变分形式，该方程由Oberai首次提出，方程右端含有体积源和面源两个声源项[15-16]：

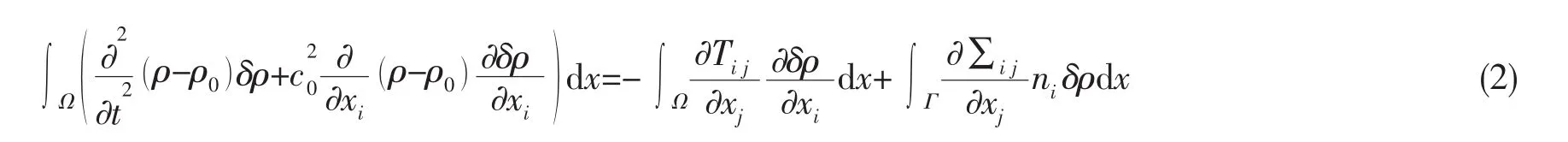
式中：Tij被称为Lighthill应力张量；c0代表声速；Ω为积分体；Γ为积分面；δρ为有限元测试函数；∑ij为总应力张量，定义为：

声场的求解过程是提取LES非定常计算时记录的每一时间步长各节点上的声源强度信息，将其插值到声场网格声源区节点，经傅里叶变换获得不同频率下声场强度及声辐射场信息。

4 结果与分析

4.1 陷落腔流场及声场分析

4.1.1 非定常流动

在流动过程中，腔体内主要有1个顺时针旋转的中心大涡和4个腔体拐角处的角涡，如图4所示，这些涡稳定的存在于腔内，始终不断重复出现涡的运动、发展、耗散和传递过程。当腔体流动进入一定的准周期，由于腔体导边存在台阶，使得流动分离并形成涡流。腔体内大部分空间由较稳定的大涡占据，该大涡在向下游运动的过程中不断发展合并，大涡尺寸不断增大。当大涡运动到腔体随边发生碰撞时，一部分流出腔外，随边界层流体一起向下游流动，另一部分破碎形成小涡向前回流，并逐渐融入底部。与此同时，腔体导边生成小涡并不断发展形成新的大涡结构，进入下一个运动周期。

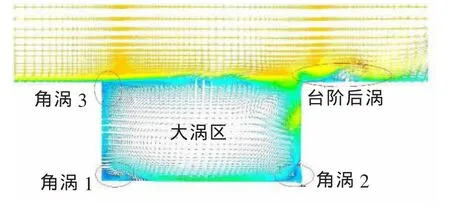
图4 陷落腔速度矢量图Fig.4 Instantaneous velocity vector of cavity

图5 陷落腔近场声源强度分布Fig.5 Source intensity of cavity in the near-field

图6 陷落腔辐射声场分布Fig.6 Radiated noise distribution of cavity

4.1.2 辐射声场特征如图5，陷落腔近场声源集中分布在随边台阶附近，

腔内以及下游边界层也有一定的噪声源存在。图6为陷落腔辐射声场特性，近场声压最大值出现在陷落腔随边台阶附近，辐射噪声传播呈现出偶极子特征，即沿上、下游方向辐射的噪声强度明显高于腔体上方。由于腔内声源强度并不是均匀分布，造成上游辐射噪声略高于下游。陷落腔声源分布以及辐射声场特征与其非定常流动规律吻合。

4.1.3 辐射噪声主要成因

通过4.1.1及4.1.2的分析不难发现，陷落腔的腔内流动非常复杂，充满多种形式的涡流。这些涡流的产生、发展、合并、破碎以及相互扰动，是陷落腔涡流噪声形成的诱因。Rossiter[6]研究表明，孔腔流动发声的根源在于其自持振荡。孔腔自持振荡包括三种形式：流体-动力振荡、流体-共振振荡、流体-弹性振荡。张楠等人[17]对刚性壁面的三维陷落腔进行研究，得到其自持振荡形式完全由流体动力振荡引起。陷落腔涡流噪声归根到底是由脉动剪应力、脉动压力与脉动速度构成的偶极子声源与四极子声源产生。Larsson等人[9]证实了脉动压力引起的偶极子声源对辐射噪声的贡献占绝对优势。本文的分析结果与以上学者的研究成果吻合，并分析了脉动压力与涡流及涡流噪声的相关性，进而阐述脉动压力与涡流运动的对应关系以及涡流噪声与涡流动力振荡的联系。

4.2 脉动压力分析

4.2.1 脉动压力分布特性

图7显示了沿流动方向陷落腔中截面脉动压力监测点布置图，其中0～1部分为1D长度，表征陷落腔口上游流场区域，1～2部分表征陷落腔导边，2～3部分表征陷落腔底边，3～4表征陷落腔随边，4～5部分为2D长度，表征陷落腔口下游流场区域。图8为陷落腔中截面脉动压力系数沿流向的分布特性。脉动压力系数定义为：

其中，p′x,（）t为压力脉动量，ρ为流体密度，U∞为流体平均流速。

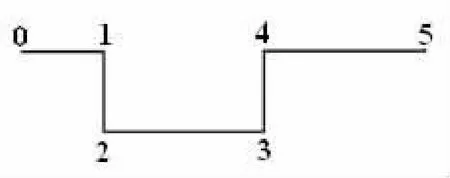
图7 陷落腔中截面脉动压力监测点布置图Fig.7 Monitoring points of wall pressure fluctuation inthe cross section of cavity

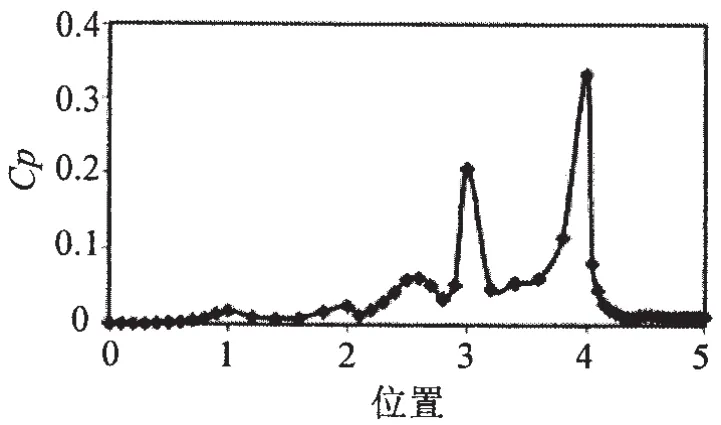
图8 陷落腔中截面脉动压力系数流向分布Fig.8 Coefficient of wall pressure fluctuation in the cross section of cavity along the streamwise direction

如图8，沿流动方向，整个随边的脉动压力系数均较大，并在随边出腔点（位置4）达到最大值，其次为陷落腔的底边，陷落腔上游、导边以及陷落腔下游脉动压力系数变化较为平缓。该模拟结果与姚熊亮等人[18]对陷落腔脉动压力分布的验证结果基本吻合。脉动压力系数的变化与其各自的位置密切相关，随边出腔点（位置4）脉动压力系数最大是由于涡旋经历生长合并后，在此处碰撞破碎，同时在陷落腔下游再次形成二次涡流，导致该位置压力变化剧烈且幅值波动较大。

4.2.2 脉动压力与涡流相关性分析

由4.2.1的分析可知，监测点4的涡流运动较为剧烈，脉动压力较大，因此针对该监测点进行详细分析。图9所示为监测点4外的脉动压力随时间步的变化曲线，从图中可以看出，时间步长0～20 000（即0～0.2 s）内，流体流动尚不稳定，脉动压力波动较大。时间步长大于20 000后（即流动时间大于0.2 s），流体流动稳定，呈现近似的周期性的变化规律。图10为流动稳定阶段两个相邻波峰时刻 （对应图9中波峰A、C两时刻）监测点4附近涡量分布图。从图10中可以发现，A、C两个时刻基本上都反映出涡流到达随边对壁面进行挤压的状态，符合周期性运动变化。而从时间的角度，A时刻对应时间为0.315 s，C时刻对应时间为0.420 s，则可以估算涡流运动变化的周期与频率分别为Δt=tA-tC=0.420 s-0.315 s=0.105 s， f=1/Δt=9.52 Hz。

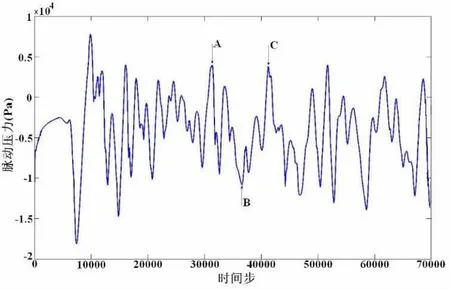
图9 监测点4脉动压力随时间步变化曲线Fig.9 Wall pressure fluctuation change with time step of monitor 4

图10 不同时刻监测点4涡量分布Fig.10 Vorticity distribution of monitor 4 in different time

为建立脉动压力与涡流运动的对应关系，将脉动压力稳定段视为平稳的随机过程，对监测点4的脉动压力进行快速傅里叶变换（FFT），得到0～100 Hz的脉动压力功率谱密度，如图11所示。该脉动压力功率谱密度所对应剪切层流体动力振荡的前三阶频率分别为f1=10.53 Hz，f2=26.32 Hz和 f3=39.47 Hz。 其中一阶频率与其涡流运动变化频率（9.52 Hz）基本吻合。

为从机理角度分析陷落腔流体动力振荡问题，不考虑流速与陷落腔结构的影响，并与经典文献相比较，引入无量纲的斯特哈劳哈尔数（Strouhal数）。将流体动力振荡频率转化为无量纲形式，与经典文献对比验证。St数的定义为：

其中，f为不可压缩流动振荡频率，L为陷落腔的特征长度，U∞为流体平均流速。则其对应的剪切层流体动力振荡的St数为St1=0.45，St2=1.13，St3=1.69，与Rossiter[6]在低马赫数时陷落腔剪切层振荡基频的预测结果St1=0.42比较接近。由于数值计算存在一定的误差，故本文结果比文献中试验结果略大。

4.2.3 脉动压力与涡流噪声相关性分析

为得到陷落腔涡流噪声声功率谱，在整个无限元区域对陷落腔的声功率监测，以得到所有声源的噪声辐射，进而探讨涡流噪声与脉动压力的相关性。图12为陷落腔10～10 000 Hz的声功率频谱，从图12可以看出，随着频率的增加，声功率明显下降，尤其是1 000 Hz以上的高频段下降有30 dB之多。原因是，陷落腔激发的涡流噪声包括低频纯音和宽带连续噪音，低频纯音主要由大尺度涡运动引起，声功率较高，高频辐射噪声呈宽带特性，是小尺度涡运动变化的结果。

从图12还可以辨识声功率谱的前三阶频率为f1=10 Hz， f2=25 Hz和f3=40 Hz，对应的 St数为 St1=0.43，St2=1.07，St3=1.71。声功率的前三阶频率与流体动力振荡的前三阶频率基本吻合，从而进一步证明了刚性壁面的三维陷落腔涡流噪声是由流体动力振荡引起的，而由脉动压力构成的偶极子源对涡流噪声的贡献很大。

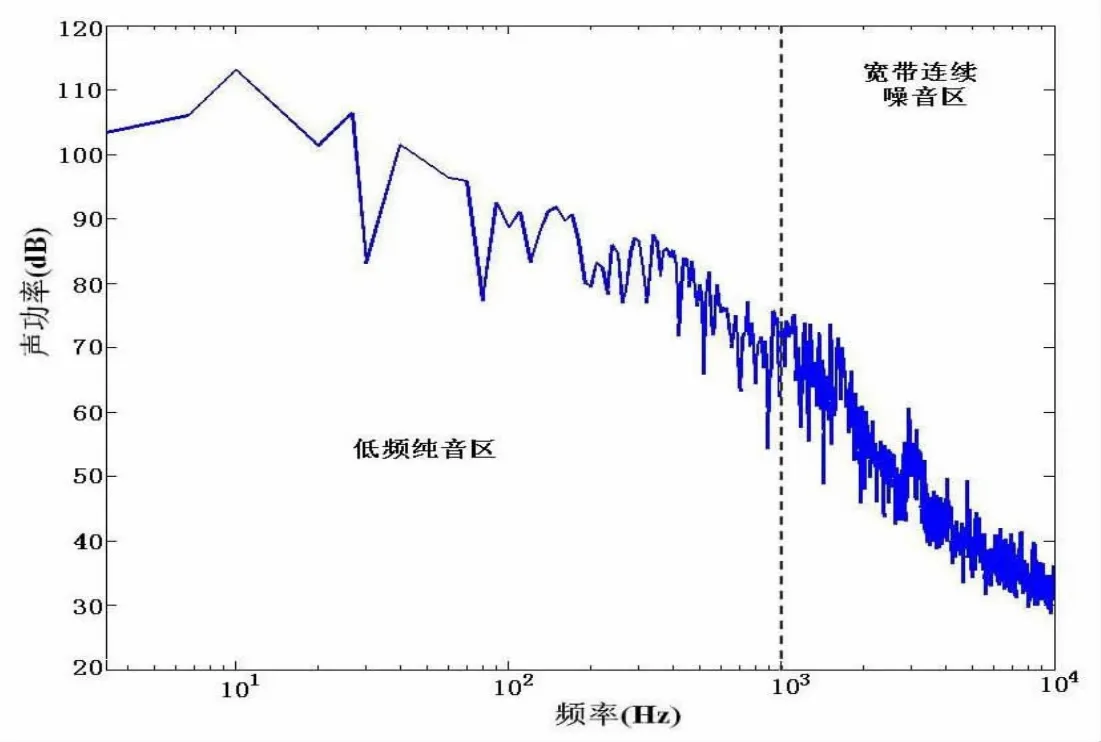
图12 陷落腔10～10 000 Hz声功率频谱Fig.12 Sound power spectrum of cavity from 10 Hz to 10 000 Hz

5 结 论

本采用LES-Lighthill等效声源法对船舶三维陷落腔流场及声场进行仿真，并对三维陷落腔流动机制、脉动压力、声功率特性进行分析，得到以下结论：

（1）陷落腔内部涡旋经历产生、发展、合并、破碎的周期性运动变化过程，不同位置的涡旋运动变化规律不同。

（2）通过对陷落腔脉动压力的分析发现，随边出腔位置脉动压力最大，并且随流动趋于稳定，其变化呈现明显的周期性。通过快速傅里叶变换，得到剪切层流体动力振荡频率谱，其基频与涡旋运动变化频率吻合。

（3）三维陷落腔涡流噪声主要表现为低频纯音及宽带连续噪音，辐射噪声呈现出偶极子特性，且声能量主要集中在低频段。通过对声功率谱的分析得到其前三阶频率与陷落腔流体动力振荡频率吻合，验证了刚性壁面的三维陷落腔涡流噪声是由流体动力振荡引起的，而由脉动压力构成的偶极子源对涡流噪声的贡献很大。

[1]何祚镛.水下噪声及其控制技术进展和展望[J].应用声学,2002,21(1):26-34.

[2]魏以迈.我国船舶水下噪声研究进展综述[J].上海造船,2001(1):27-32.

[3]汤渭霖.水下噪声学原理[M].上海:上海交通大学讲义,2004.

[4]刘应中,缪国平.高等流体力学[M].上海:上海交通大学出版社,2000.

[5]Fuglsang D C,Cain A B.Evaluation of shear layer cavity resonance mechanisms by numerical simulation[R].AIAA Paper 1922-0555,1992.

[6]Rossiter J E.Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[R].Rep.Mem.3438,Aeronautical Research Council,1964.

[7]Guiliaume A B,Colonius T.Three-dimensional instabilities in compressible flow over open cavities[J].J Fluid Mech.,2008,599:309-339.

[8]Jonas Ask,Lars Davidson,Hans Enwald,et al.An acoustic analogy applied to incompressible flow fields[C]//Computational Aeroacoustics:From Acoustic Sources Modeling to Far-Field Radiated Noise Prediction Colloquium EUROMECH 449,December 9-12,2003.Chamonix,France,2003.

[9]Larsson L,Davidson L,Olsson M,et al.Acoustic investigation of an open cavity flow at low Mach number[J].AIAA Journal,2004,42(12):2462-2473.

[10]Geng Donghan,Wang Yu.Prediction of hydrodynamic noise of open cavity flow[J].Transactions of Tianjin University,2009,15:336-342.

[11]Wang Yu,Liu Yuhong.Prediction of 3D cavity hydrodynamic noise based on equivalent source method[J].Journal of Advanced Materials Research,2011,189-193:53-56.

[12]耿冬寒,刘正先.大涡模拟-Lighthill等效声源法的空腔水动噪声预测[J].哈尔滨工程大学学报,2010,31(2):182-187.

[13]张兆顺,崔桂香,许春晓.湍流大涡数值模拟的理论和应用[M].北京:清华大学出版社,2008:95-105.

[14]Lighthill M J.On sound generated aerodynamicallyⅠ:General theory[J].Proceedings of the Royal Society of London,1952,211A(1107):564-587.

[15]Oberai A,Ronaldkin F,Hughes T.Computational procedures for determining structural-acoustic response due to hydrodynamic sources[J].Computer Methods in Applied Mechanics and Engineering,2000,190(3-4):345-361.

[16]Oberai A,Ronaldkin F,Hughes T.Computational of tailing-edge noise due to turbulent flow over an airfoil[J].AIAA Journal,2002,40(5):2206-2216.

[17]张 楠,沈泓萃,朱锡清.三维孔腔流激噪声的大涡模拟与声学类比预报与验证研究[J].船舶力学,2010,14(1-2):181-190.Zhang Nan,Shen Hongcui,et al.Validation and prediction of flow induced noise of 3-D cavity with large eddy simulation and acoustic analogy[J].Journal of Ship Mechanics,2010,14(1-2):181-190.

[18]姚熊亮,杨国晶,戴绍仕,等.陷落腔剪切层自持振荡的数值计算分析[J].水动力学研究与进展,2009,24(3):332-340.

Research on turbulent flow noise mechanism of 3D rigid cavity

WANG Yu,WANG Shu-xin,LIU Yu-hong

(School of Mechanical Engineering,Tianjin University,Tianjin 300072,China)

Turbulent flow noise generated by the 3D rigid cavity has attracted an increasing amount of attention during the past decade.In this paper,the flow field and the turbulent flow noise generated by the flow past 3D rigid cavity at Mach number 0.004 8 was simulated by LES-Lighthill equivalent sources method.The turbulence motion inside the cavity and the characteristics of the radiated noise are described vividly.By comparing the mechanism of turbulence,wall pressure fluctuations,characteristics of the radiated noise,the relationship between vortex and sound is revealed.It is found that the first three frequencies in the sound power spectrum agree with the frequencies of hydrodynamic oscillation.It is indicated that the turbulent flow noise of 3D rigid cavity is induced by the oscillation of the fluid,and the dipole source,which is constituted by the wall pressure fluctuations,makes the largest contribution to the turbulent flow noise.Achievement of this paper provides a theoretical basis for controlling the turbulent flow noise of underwater vehicle.

3D cavity;turbulent flow noise;large eddy simulation(LES);equivalent sources method;relationship between vortex and sound

TB53

A

1007-7294（2012）11-1321-08

2012-06-13

国家自然科学重点基金（50835006）和国家863计划项目（2010AA09Z102）基金资助

王 玉（1984-），女，天津大学机械工程学院博士研究生；王树新（1966-），男，教授，博士生导师；

刘玉红（1971-），女，天津大学机械工程学院副教授，E-mail:yuhong_liu@tju.edu.cn。