腐蚀损伤对深海半潜式平台结构极限强度的影响研究

张 健，沈中祥，王自力，嵇春艳

（1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2.中国船舶科学研究中心，江苏 无锡 214082））

腐蚀损伤对深海半潜式平台结构极限强度的影响研究

张 健1,2，沈中祥1，王自力1，嵇春艳1

（1.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2.中国船舶科学研究中心，江苏 无锡 214082））

极限强度是半潜式海洋平台适应环境能力的重要指标，鉴于腐蚀损伤对平台极限承载能力的重要影响，在评价平台结构安全性时应考虑腐蚀损伤因素。文章以3000 m深海半潜式平台为研究对象，运用有限元软件建立以腐蚀厚度为变量的典型构件和节点的参数化模型，基于逐步破坏分析法和有限元计算法，采用增量理论按比例逐步加载，计算了典型构件和节点在腐蚀损伤影响下的极限承载力，总结了典型构件和节点在不同失效模式和服役年限下的极限承载力演变规律。

半潜平台；腐蚀；构件；节点；极限强度

1 引 言

随着各国经济发展对油气资源的需求日益扩大，陆上油气资源的逐步枯竭，油气资源开发正在不断地向海洋尤其是深海发展[1]。而深海半潜式钻井平台作为目前国内外用于深海开发的主流钻井设备，体积庞大、结构复杂，且长期处于盐雾、潮气和海水等环境中，受到海水及海生物的侵蚀而产生剧烈的电化学腐蚀，海洋环境十分复杂恶劣，腐蚀严重影响海洋平台结构材料的力学性能，降低平台承载能力，影响平台使用安全[2]。因此，平台一旦发生事故后果不堪设想。1980年“亚历山大·基尔兰”号（Alexander L.Kielland）半潜式生活平台由于D-6撑杆在腐蚀作用下发生断裂最后导致整个平台的倾覆[3]；2001年3月巴西最大的海上平台也是当时世界上最大的半潜式海上油井平台之一，耗资3.26亿美元的老龄化平台P-36号沉没造成巨大经济损失和环境污染[4]。这些事故引起了国际海洋工程界的高度重视，国际船舶与海洋结构委员会在2003年成立了专门的"老龄化船舶与海洋结构评估委员会"，探讨老龄化船舶和平台合适的评估方法和判定标准。

平台极限强度评估是确保其在可能的极限外载荷下有足够的强度储备，是保证完整性最有效的方法。目前，研究海洋平台结构的极限强度已经成为国际海洋工程领域近期的一个热点研究课题。由于我国深水海洋平台的研究还处于起步阶段，腐蚀对深水海洋平台极限强度的研究尚未充分开展，再加上我国钢材抗腐蚀性能及防腐技术与发达国家有一定差距，因此，进行考虑腐蚀损伤下的海洋平台安全评估研究具有重要意义。

2 极限强度概述

极限强度的概念早在上世纪五十年代就由VASTA提出，极限状态是评价结构物是处于正常功能状态还是处于失效状态的衡量标准。所谓极限分析，就是当外载荷达到某一极限值，结构将变为几何可变机构，变形将无限制地增长，从而失去承载能力，这种状态称为结构的极限状态。当研究极限状态时的应力、应变、载荷或变形等时，即为极限分析。根据结构物的种类、使用目的和使用方式的不同，可分为多种极限状态。即使对于同一种极限状态，其失效模式也不尽相同。通常情况下可分为三种极限状态：最终极限状态、可服务性极限状态和条件性极限状态。

本文基于逐步破坏法原理，采用非线性有限元计算方法求解结构的极限强度，采用弧长法[5]求解过程中，考虑几何和材料非线性的影响，通过改变单元大小、载荷步长、边界条件等影响结果精度的因素，获得平台在考虑腐蚀损伤下典型构件和节点的极限承载力。

3 腐蚀预报模型

海洋平台结构的腐蚀机理极为复杂，很难用理论化的数学模型进行详尽描述。目前，在船舶与海洋结构物的腐蚀缺陷分析中，通常以结构物在修复期内的任意一个时刻，板厚以某种形式的减少来表示腐蚀的影响。各国学者根据结构类型的环境、材料特性等提出各类的腐蚀数学模型。Southwell等人[5]提出了一个线性和双线性的模型。Melchers[6]在统计分析后将该模型参数表示成统计意义上的关系，从而将这两个模型发展成“拓展的Southwell模型”，并进一步提出了指数模型。这些模型可简要地归纳如下：

拓展的Southwell线性模型：

Melchers-Southwell指数模型

Melchers还提出了三线性和另一种指数模型

Melchers三线性模型

Melchers指数模型

其中,d（t）是将t时刻腐蚀了的板厚作为确定的量时的值；u（t）和σ（t）是t时刻腐蚀了的板厚作为不确定的均值和标准方差。Duedes和Paik模型中考虑了腐蚀保护系统 （Corrosion Protection System,CPS）对板厚变化的影响，然而，这个模型中认为腐蚀过程在CPS完全失效时才开始，并没有考虑腐蚀保护系统和环境的相互作用。事实上，腐蚀保护系统比如防腐涂层是一个渐进失效的过程，在其完全失效之前腐蚀就已经开始了。考虑到腐蚀保护效能的逐渐衰减及附着微生物等条件的影响，秦圣平提出用 Weibull方程来描述腐蚀速率[7]：

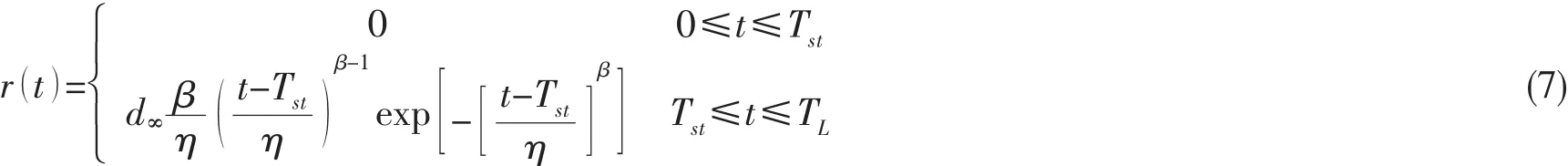
式中：d∞，β，η，Tst四个待定系数可以根据 Paik[8]等人提供的腐蚀数据分布规律确定，如（8）式，腐蚀速率和腐蚀厚度与时间的关系如图1和图2所示。

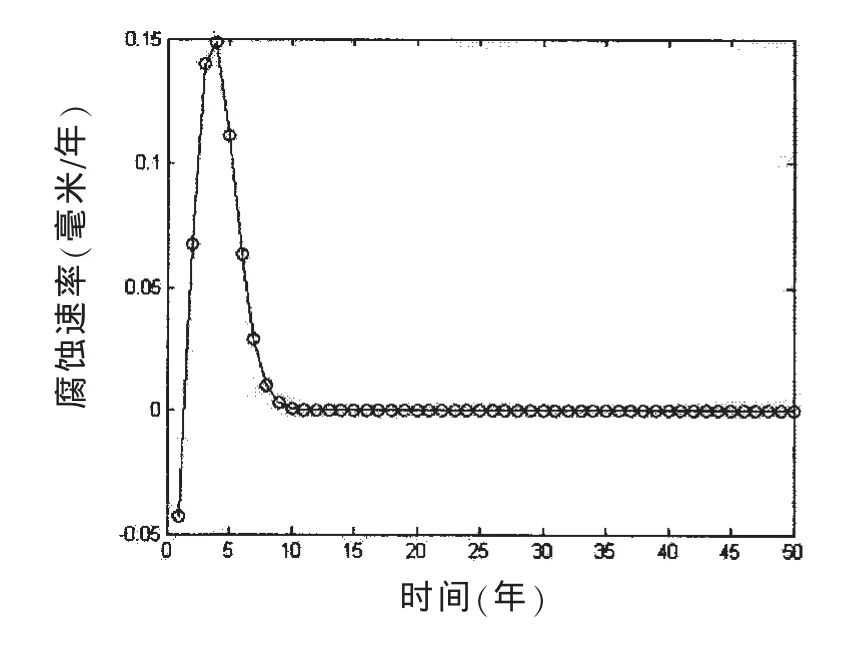
图1 腐蚀速率曲线Fig.1 Corrosion rate curve

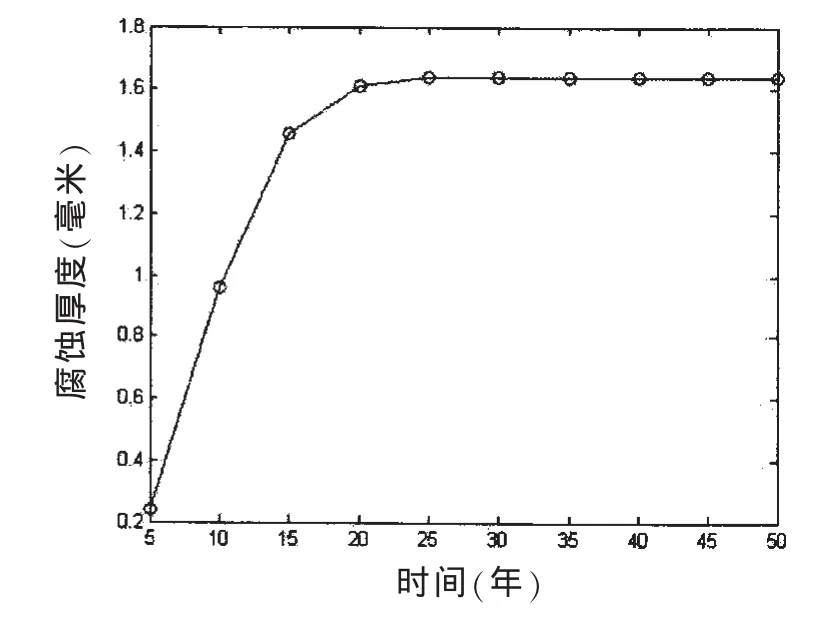
图2 腐蚀厚度曲线Fig.2 Corrosion thickness curve

（8）式所示模型是根据Paik所提供的散货船纵向构件所拟合出的腐蚀曲线，他考虑了CPS的逐渐失效过程，存在腐蚀加速、减速阶段，避免了腐蚀速率的跃变过程，具有较好的拟合性。由于本文研究目标为平台结构的极限强度，需要预报出该结构在最恶劣条件下的最大承载能力，不同海域海水盐度、温度和生物附着情况不同，海水对结构的侵蚀能力不同，导致平台腐蚀保护有效度和腐蚀速率也会有所不同。因此，腐蚀模型需要包括各种最恶劣腐蚀情况，为了揭示腐蚀对平台结构极限强度的影响，本文算例采用没有任何腐蚀保护的腐蚀模型，如下式所示[9]。

式中：r（t）为t时间内材料厚度的损失(mm)；ri为平均年腐蚀率(mm/年)；t0为防腐材料的保护时间。 假设在同一区域内，构件年腐蚀率相同。计及海水对水下构件及水上构件腐蚀速率的影响，本文根据各种腐蚀模型的年平均腐蚀量，确定腐蚀速率如表1所示。

表1 腐蚀速率的统计特性Tab.1 Probabilistic characteristics of corrosion rate

4 腐蚀损伤下典型构件和节点极限承载力数值仿真

4.1 典型构件和节点的选取

在进行海洋平台极限承载力计算之前，首先需要对各种海况条件下海洋平台的整体受力模式及结构响应进行分析，从而确定在常规海况下海洋平台的结构受力特点和构件失效模式，以便进一步确定选取何种受力状态下的何种构件和节点进行极限强度分析。本文依据我国最新的3000米深水半潜平台图纸，建立包括平台主体、立柱、下浮体、横撑等主要部分的半潜式平台整体结构的有限元模型，并对其在各种海况下的应力分布状况进行计算分析，计算结果如图3所示。在进行极限强度分析时，应选取应力最大部位作为极限强度研究对象。就构件而言，在下浮体与下浮体、立柱与立柱、立柱与平台之间设置的撑杆一方面加强了平台的强度，同时由于其受力状态复杂，撑杆是平台中较易发生破坏的构件，属平台结构中的薄弱环节；就节点而言，横撑与立柱交界处节点应力集中较为严重，在各类节点中属于易首先发生失效的部位，因此，最终确定横撑作为典型构件、横撑与立柱交界处节点作为典型节点进行极限强度分析。

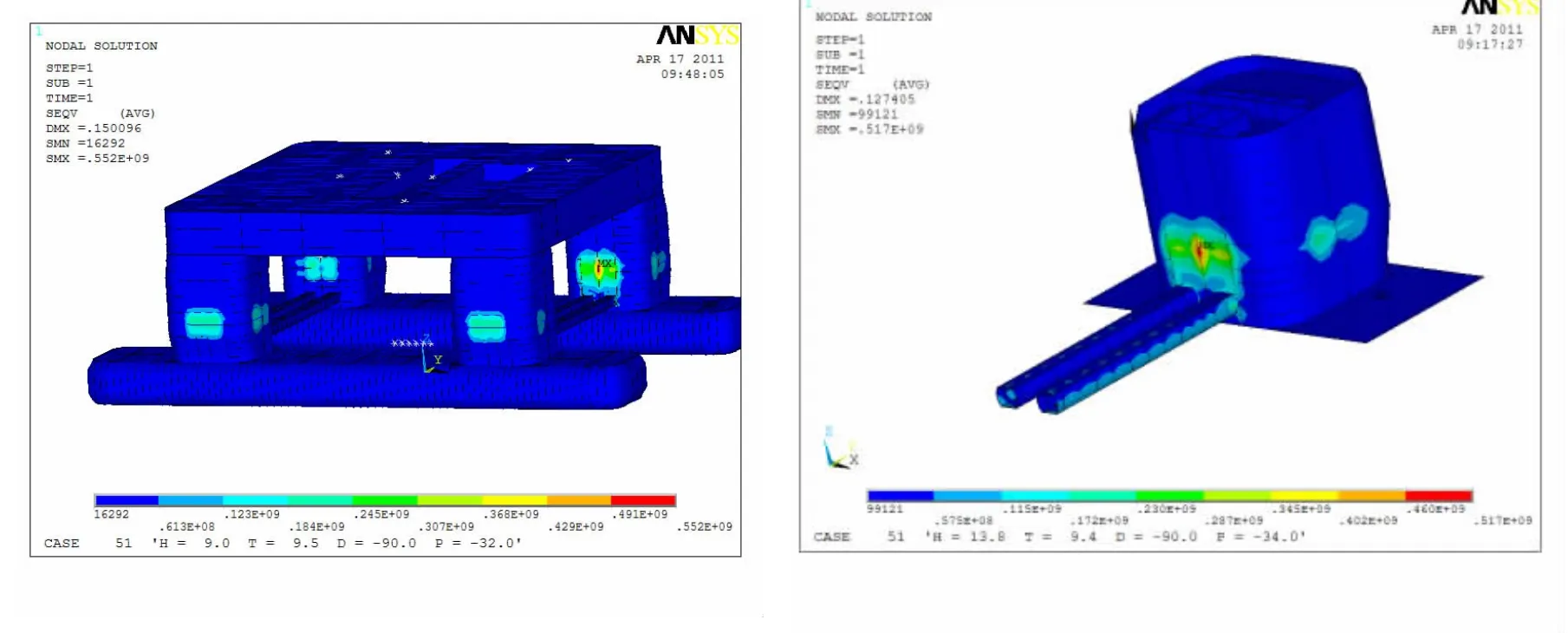
图3 整体半潜式平台应力分布Fig.3 Stress distribution of the semi-submersible platform

4.2 有限元模型概述

该平台材料为EQ36钢材，屈服强度为355MPa，密度为7 800 kg/m3，泊松比为0.32，弹性模量为206GPa。

建立典型构件（横撑）有限元模型时，由于横撑跨度较大，且为左右对称结构，为减小计算量，典型构件取其长度一半进行参数化建模，中部端面采用对称约束，为更加准确模拟立柱对横撑的约束，在横撑与立柱相交一端建立立柱板，并将约束施加于立柱板四周的刚性周界上，有限元模型如图4所示。为消除边界条件的影响，建立典型节点有限元模型时，将立柱上端取横撑往上1m，下端与浮体甲板相交，横撑向立柱外测延长2个肋位距离，内侧延长1个肋位距离，立柱上下端采用刚性约束。由于载荷施加处结构由壳单元和梁单元两种类型的单元构成，为解决不同类型的单元之间的载荷传递，端部采用MPC进行边界处理。典型节点有限元模型如图5所示。

图4 典型构件（横撑）有限元模型Fig.4 Finite Element Model of the typical component

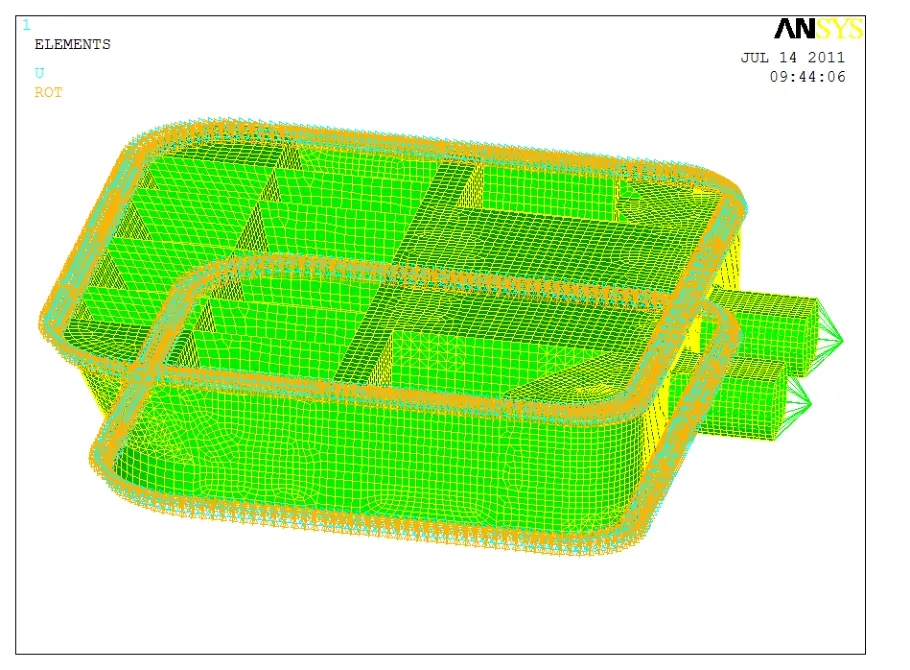
图5 典型节点有限元模型Fig.5 Finite Element Model of the typical node

首先对结构进行一阶模态屈曲分析，得到结构的理论屈曲强度（分叉点），将理论屈曲值的2-2.5倍作为载荷施加于结构上，进行典型构件和节点极限承载力计算。

4.3 典型构件和节点失效模式

经过对半潜平台进行整体应力分析，结果表明，横撑和节点的受力方式主要有轴向受压、受弯以及受剪，在多数情况下构件和节点属于多种受力状态联合作用，而且在平台受到不同海况作用下，横撑和节点的主受力方式不同。计算结果表明，横撑的主受力方式为弯曲，典型节点的主受力方式为剪切。

本文在极限承载力计算过程中，首先分别计算了横撑和节点在服役0年（无损状态）轴向受压、纯剪切状态和弯曲状态下的极限承载力。同时，为了进一步研究不同服役年限下结构腐蚀对横撑极限承载力的影响，分别计算横撑在服役10年、20年、30年、40年和50年时弯曲状态下的极限承载力；分别计算节点在服役10年、20年、30年、40年和50年时剪切状态下的极限承载力。

4.4 无损状态下横撑和节点极限承载力计算结果

无损平台极限强度评估是剩余极限强度评估的基础，采用弧长法分别计算横撑和节点在服役0年（无损状态）平台受弯、受剪和受压3种失效模式下的极限承载力，计算结果如图6-11所示，结果汇总表见表2。

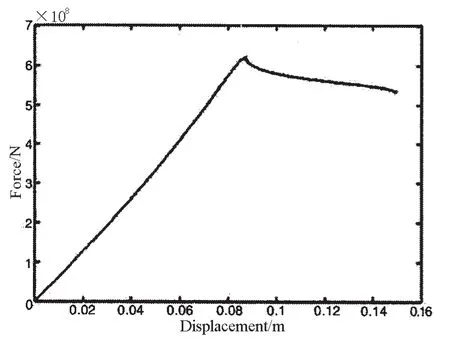
图6 横撑无损受压荷载曲线Fig.6 Curve of typical component without defects under the compression action

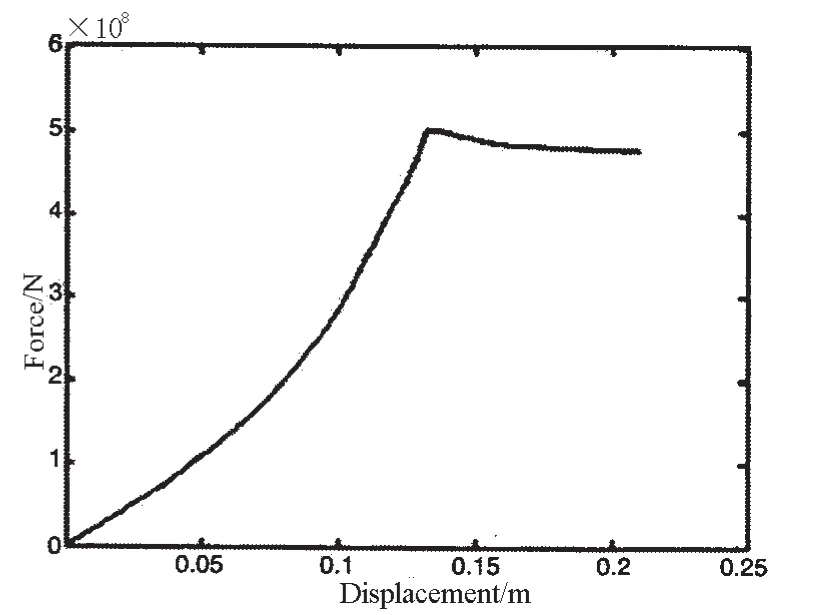
图7 典型节点无损受压荷载曲线Fig.7 Curve of typical node without defects under the compression action

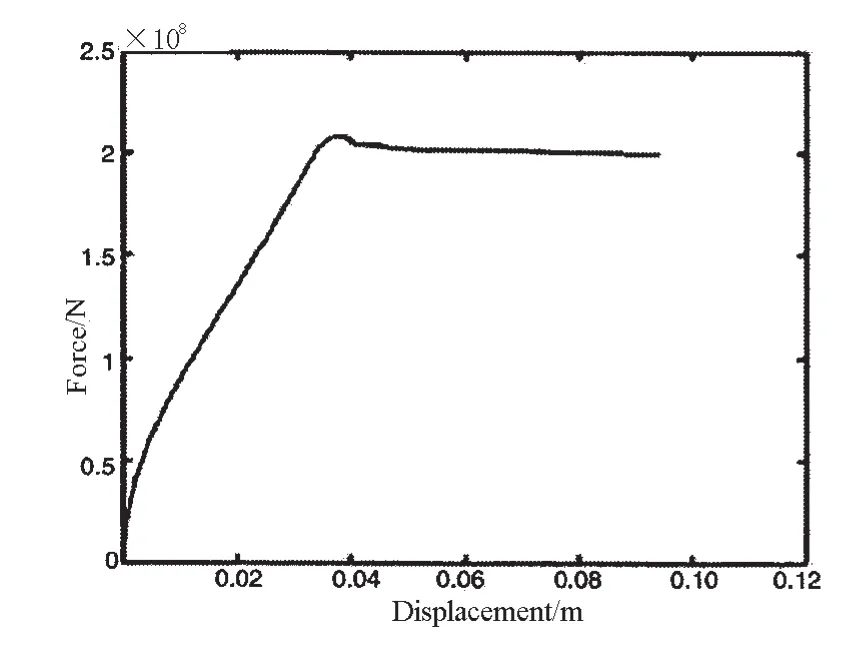
图8 横撑无损受剪荷载曲线Fig.8 Load curve of typical component without defects under the shear action

图9 典型节点无损受剪荷载曲线Fig.9 Load curve of typical node without defects under the shear action

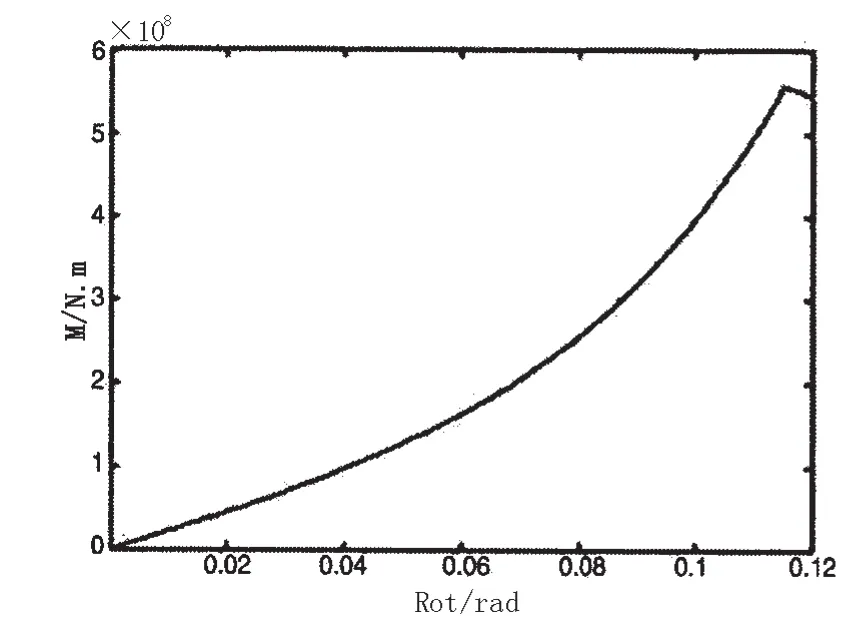
图10 横撑无损受弯限荷载曲线Fig.10 Load curve of typical component withoutdefects under the bending action

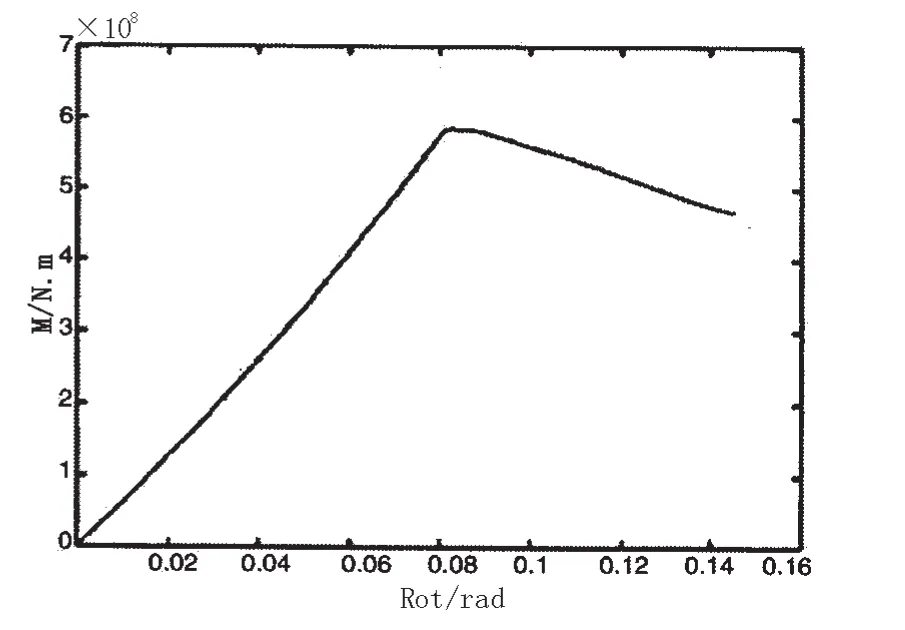
图11 典型节点无损受弯荷载曲线Fig.11 Load curve of typical node without defects under the bending action

表2 横撑和节点无损时在压缩、剪切和弯曲作用下的极限载荷Tab.2 The limit load of typical component and node without defects under the action of compression,shear and bending

研究各种受力模式下横撑和节点的极限荷载曲线可知，各条曲线有一个共同特点，即在外载荷不断增加的同时，结构变形也逐步增加，当外载荷达到某一峰值后荷载随即开始下降，而结构变形将无限制地增长，此时结构逐渐丧失承载能力，该荷载峰值对应状态即为结构极限强度状态。对不同受力模式下的曲线形状比较可以看出，相比而言，横撑及节点在受压和受弯模式下的荷载曲线在达到峰值后下降曲率较大，承载力下降迅速，而受剪模式曲线下降曲率较小，卸载速度较为缓慢，这说明无论横撑还是节点，剪切破坏模式对结构的极限强度的影响较为稳定，而在压缩和弯曲受力模式下，结构一旦达到极限强度其承受风浪流等外载荷的能力将迅速下降。将典型构件横撑和典型节点的极限载荷图进行比较可以发现，三种受力模式下横撑的极限荷载曲线在峰值位置处均有一个明显凸起，说明横撑在达到极限荷载后先是有一个明显卸载然后再趋于平缓，这与横撑相对节点而言结构较弱有关，同时与横撑和节点的约束条件不同有关。

考察横撑及典型节点到达极限强度状态时的应力分布，可以发现，无论是受剪、受压还是受弯模式，节点达到极限状态时最大应力发生在横撑与立柱连接的端部，横撑达到极限状态时的最大应力同样发生在靠近横撑端部的部位，横撑中部区域应力相对较小，如图12和图13所示，因此，在平台设计及建造时应注意对该区域的结构加强，在平台使用过程中也应特别注意对该部位的定期检查和维护。

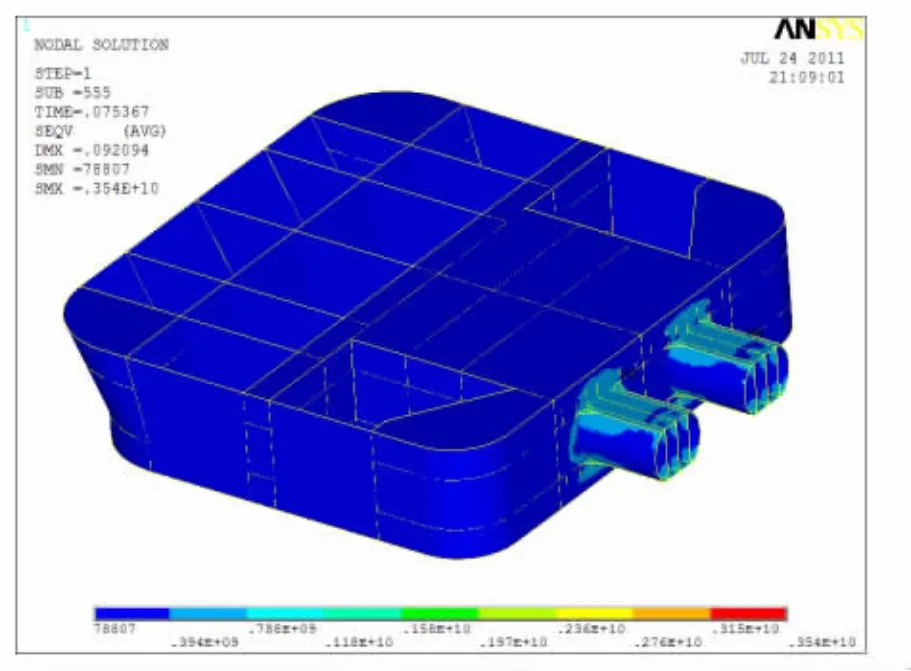
图12 典型节点达到极限状态时应力分布Fig.12 Stress distribution of typical node

图13 典型构件达到极限状态的应力分布Fig.13 Stress distribution of typical component

4.5 不同服役期年限下典型构件和节点极限承载力计算结果

海洋平台除了外部暴露在海洋环境中会发生材料腐蚀外，部分内部结构尤其是液舱结构也会发生不同程度的腐蚀，在进行强度计算时应予考虑，鉴于本文所分析的是典型构件和节点的具体位置，故不考虑结构内部腐蚀影响。本文采用前文所述腐蚀模型，以结构构件厚度的非线性衰减来表示腐蚀的影响，采用弧长控制法计算横撑和节点受腐蚀损伤影响。由于平台在斜浪及迎浪状态时时常处于波峰位于浮体中部或波谷位于浮体中部的情况，从而使平台处于中拱或中垂状态，加之横撑属于细长型构件，较之于其他受力模式，弯曲是横撑的主受力状态，故需考察横撑在不同服役年下的受弯的极限荷载。典型节点属于横撑端部与立柱连接的局部结构，结构较强且长度较小，就压缩、剪切和弯曲三种受力模式相对而言，剪切为其主受力状态，故考察节点在不同服役年下受剪切的极限荷载。计算结果见表 3、表 4及图 14、图 15。

表3 不同服役年时横撑腐蚀损伤下的极限强度Tab.3 Ultimate strength of typical component with corrosion damage in different years

表4 不同服役年时典型节点腐蚀损伤下的极限强度Tab.4 Ultimate strength of typical node with corrosion damage in different years

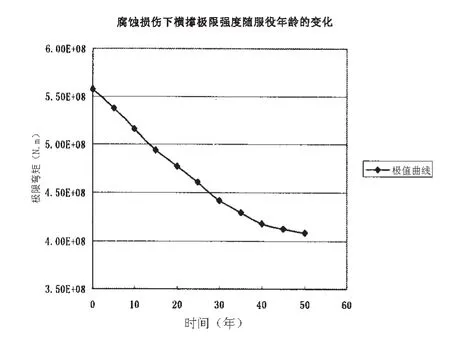
图14 横撑在不同服役年限下的极限强度Fig.14 Ultimate strength of typical component in different years

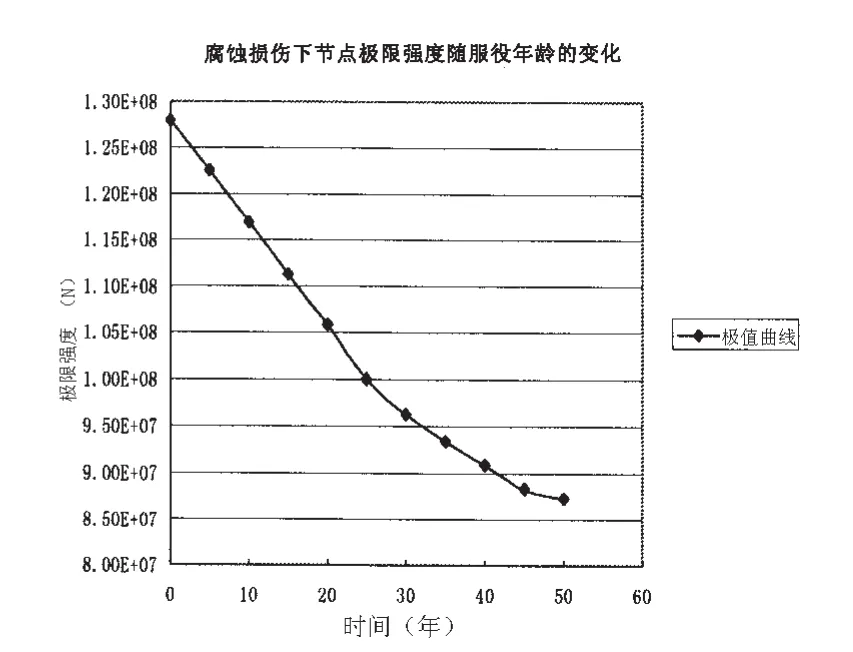
图15 典型节点在不同服役年限下的极限载荷Fig.15 Ultimate strength of typical node in different years

对计算结果进行分析可以看出，腐蚀损伤对深海半潜式平台的极限承载力具有重要影响，典型构件及典型节点的极限承载力随着服役年限增加而近似呈线性降低，且前30年极限承载力下降较快，30年后下降速率相对平缓。对横撑而言，前30年中每10年的极限承载力损失约为服役0年时极限承载力的7%左右，30年以后每10年的极限承载力损失约为服役初期极限承载力的4%左右，且有愈加平缓的趋势。典型节点也具有相同的规律，前30年每10年其极限承载力损失8.5%，30年后每10年损失约5.1%。分析产生这一现象的原因，是因为平台结构外表面暴露于海洋环境中腐蚀严重，内部结构不直接与海洋环境接触，可以忽略其腐蚀损伤。因此，前30年外板对整个结构的极限承载力贡献较大，外板厚度的损失对整个结构极限强度的比重较大，而随着时间的推移，外板逐渐变薄，结构的内部构件对极限承载力的贡献逐渐加大，外板厚度的损失对极限承载力的影响所占比重逐渐减小，故而出现30年后极限承载力曲线渐趋变缓的现象。

在不考虑腐蚀保护的前提下，在平台服役50年后，平台关键构件及典型节点的极限承载力与服役0年相比下降约30%左右。可见腐蚀损伤对平台的关键构件和节点的极限承载力有着重要影响，这种损伤缺陷可在一定程度上减小构件和节点的强度或者放大荷载的作用，从而最终影响结构的安全性，因此在深海半潜式平台全寿命周期内，平台的定期维修和腐蚀保护应予以特别关注。

5 结 语

通过对深海半潜式平台典型构件和节点在腐蚀损伤下极限强度的研究分析，总结出腐蚀损伤对平台极限承载力的影响及随时间的演变规律，可以得出如下结论：

（1）海洋平台整体强度分析表明，深海半潜式海洋平台的横撑及横撑与立柱相交的交贯线区域是平台的薄弱部位及应力集中区域，易首先达到极限载荷，横撑的主受力模式为弯曲，典型节点的主受力模式为剪切，在设计中应对此类区域采取相应的结构设计。

（2）腐蚀损伤对平台的典型构件和节点的极限承载力有重要影响，单纯考虑腐蚀损伤的影响，极限承载力随着服役年限的增加而近似呈线性降低，服役期内的前30年下降尤其迅速，这种损伤与疲劳等多种载荷联合作用会降低构件和节点的强度而放大荷载的作用，从而最终影响结构的安全性，因此平台全寿命期内，对海洋平台结构进行长效防腐、进行定期防腐维护对于提高海洋平台的极限强度至关重要。

[1]张 帆，杨建民，李润培.spar平台的发展趋势及其关键技术[J].中国海洋平台，2005，20（2）:6-11.

[2]吴宇新.腐蚀条件下抗冰海洋平台疲劳分析[D].大连:大连理工大学，2007.

[3]Torgeir Moan.The Alexander L Kielland accident[C].Proc,The First Robert Bruce Wallace Lecture,Dept.of Ocean Engineering,Massachusetts Institute of Technology,April,1981.

[4]刘志刚.GM_Lift半潜式平台立柱的结构设计与强度分析研究[D].上海:上海交通大学，2006.

[5]Southwell C R,Bultman J D,Hummer Jr C W.Estimating of service life of steel in seawater[M].In:Schumacher M,editor.Seawater Corrosion Handbook.New Jersey:Noyes Data Corporation,1979:374-387.

[6]Melchers R E,Ahammmed M.Nonlinear modeling of corrosion of steel in marine environments[R].Research Report 106.09.1994,Department of Civil Engineering and Surveying,The University of Newcastle,1994.

[7]秦圣平，崔维成，沈 凯.船舶结构时变可靠性分析的一种非线性腐蚀模型[J].船舶力学,2003,7(1):94-102.Qin shengping,Cui Weicheng,Shen Kai.A nonlinear corrosion model for time variant reliablity analysis of ship structure[J].Journal of Ship Mechanics,2003,7(1):94-102.

[8]Paik J K.Residual ultimate strength of steel plates with longitudinal cracks under axial compression-nonlinear finite element method investigations[J].Ocean Engineering,2009,36(3-4):266-276.

[9]Melchers R E.Corrosion uncertainty modeling for steel structures[J].Journal of Constructional Steel Research,1999,52:3-19.

Influence research of ultimate strength to deepwater semi-submersible platforms structure under corrosion damage

ZHANG Jian1,2，SHEN Zhong-xiang1，WANG Zi-li1，JI Chun-yan1

(1.School of Navy architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China;2.China Ship Scientific Research Center,Wuxi 214082,China)

Ultimate strength is an important indicator of the adaptability to changing environment of semi-submersible platforms.As corrosion damage has significant effects on the ultimate strength,the corrosion damage factor should be taken into account in the platforms structural safety evaluation process.Taking 3000m deep sea semi-submersible platforms as research objects,the parameterized model of typical component and node is established taking corrosion thickness as variable used the finite element software.Based on the gradually damage calculation method and finite element analysis method,the load is increased progressively according to proportion increment theory.The ultimate bearing capacity of typical component and node is calculated under the corrosion damage.The ultimate bearing capacity evolution law of typical component and node under various failure modes and various service years is summarized.

semi-submersible platform；corrosion；component； node；ultimate strength

U661.43

A

1007-7294（2012）11-1283-08

2012-06-09

国家自然科学基金资助项目（50609009）；江苏省船舶先进设计制造技术重点实验室开放研究基金资助课题（CJ0806）。

张 健（1977-），男，江苏科技大学船舶与海洋工程学院副教授,博士研究生;

沈中祥（1985-），男，硕士生。