基于熵限制的Baldwin-Lomax湍流模型

赵 瑞 阎 超 于 剑

（北京航空航天大学 航空科学与工程学院，北京 100191）

基于熵限制的Baldwin-Lomax湍流模型

赵 瑞 阎 超 于 剑

（北京航空航天大学 航空科学与工程学院，北京 100191）

针对Baldwin-Lomax（BL）模型在模拟超声速复杂流动中的不足，提出一种基于熵限制的新型修正方式.分别采用原始的BL模型（BL-origin）、修正后的BL模型（BL-entropy）以及Wilcox k-ω两方程模型对超声速平板、超声速二维压缩拐角以及膨胀-压缩拐角3个典型算例进行计算，结果表明BL-entropy能够较好地获取长度尺度进而得到均匀合理的涡粘性分布.同时，该修正方式简单高效并且适用于其他与超声速边界层有关的模型，具有较大的发展潜力.

湍流模型;熵;超声速流动;计算流体力学

超声速飞行器在大多数飞行情况下都处于湍流流态.由于湍流是流体微团的不规则运动，湍流运动产生的质量、动量和能量的输运将远远大于分子热运动产生的宏观输运，同时湍流脉动导致额外的能量耗散，引起气动加热和摩阻增加.此外，高超声速流动中普遍存在激波与湍流边界层相互作用、激波诱导边界层分离与再附等非常复杂的现象，因此湍流计算对准确预估高超声速飞行器的气动性能非常重要.

目前湍流数值模拟一般有3种方法:直接数值模拟（DNS，Direct Numerical Simulation），大涡模拟（LES，Large Eddy Simulation），雷诺平均 N-S方程（RANS，Reynolds Average Navier-Stokes）.受目前计算机条件等限制，前两种方法只限于求解一些低雷诺数的简单流动，RANS只计算大尺度平均流动，所有湍流脉动对平均流动的作用均用模型假设封闭，使计算量大为减少，其中 BL（Baldwin-Lomax）零方程湍流模型构造最简单、鲁棒性最好、精度较高，在工程界应用最广泛.

原始的BL模型［1］在工程计算中存在的不足主要表现在:强逆压梯度非平衡湍流边界层;分离区附近及内部流动;激波/边界层干扰;超声速及高超声速激波附近存在剧烈涡量变化的流动等.为此，研究学者针对具体的流动工况提出了不同的修正方式:文献［2］针对大分离漩涡流动提出Degani-Schiff修正;文献［3］指出该修正的物理缺陷，并提出Kcut修正，但仍然存在如何确定Kcut点位置的问题;文献［4］针对后掠激波/边界层干扰流动提出Panaras修正，该方法必须人为指定分离前参考点;与此类似，文献［5］提出的松弛模型也是通过人为指定参考点引入上游历史效应，显然这种修正方式在实际工程运用中受到限制.

针对超声速复杂流动，本文引入熵限制的概念，试图在不增加原始BL模型复杂度的前提下，提高BL模型的预测精度，使之更好地适于工程运用.为检验该修正方式的效果，分别采用原始的BL模型（BL-origin）、修正后的BL模型（BL-entropy）及两方程 Wilcox k-ω［6］模型对超声速平板、超声速压缩拐角、超声速膨胀-压缩拐角进行数值模拟，并对这种新型的修正方式做出综合评价.

1 数值方法

1.1 控制方程

基本控制方程为雷诺平均N-S方程，其守恒形式为

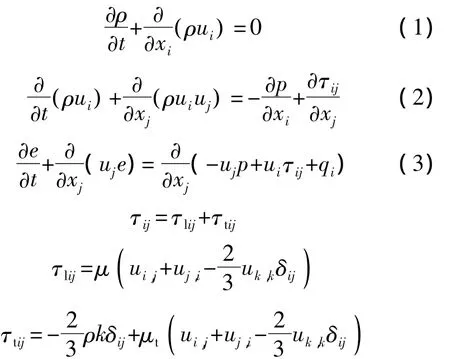
其中，τtij为雷诺应力，对于μt模化方法不同，构造不同的涡粘性湍流模型.

采用有限体积法求解N-S方程，计算采用量热完全气体假设，粘性通量采用中心差分格式进行离散，无粘通量的离散选择Roe的FDS（Flux Difference Splitting）格式，时间推进采用LU-SGS（Lowerk-Upper Symmeffic Gauss-Seidel）隐式方法.

1.2 湍流模型

BL模型对湍流边界层的内层与外层采用不同的混合长假设，其涡粘性如下所示:

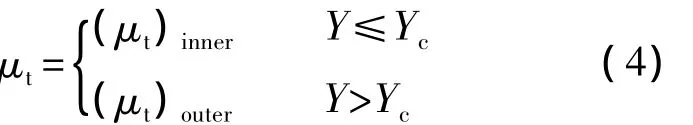
其中，Yc是（μt）inner=（μt）outer时 Y 到壁面最小距离.

对于内层，即Y≤Yc，有:

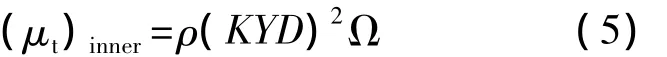
其中，ρ为密度;Ω为涡量;K=0.4为 Karman常数;Van Driest衰减因子D如下:

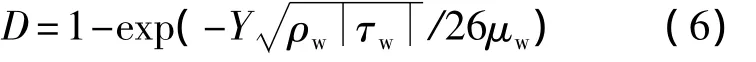
其中τw为壁面摩擦力.

对于外层，即 Y＞Yc，有:

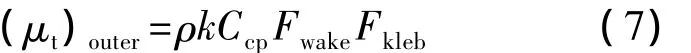
其中，k=0.0168;Ccp=1.6.

尾迹函数Fwake如下式所示:

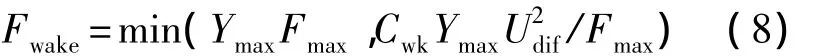
其中 Fmax=max（YΩD）;Ymax是函数 F=YΩD 达到最大值Fmax的位置;Cwk=1.0;Udiff是平均速度分布中最大值与最小值之差.

Klebanoff间歇函数Fkleb如下式所示:

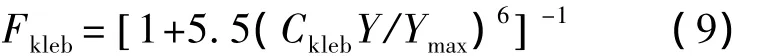
其中，Ckleb=0.3;边界层厚度 δ=Ymax/Ckleb.

大量研究表明，原始的BL模型只能准确地预测附体流动以及弱分离流动，对于激波/边界层干扰以及分离、再附等复杂流动却无能为力.究其根本原因，一方面BL模型中的经验常数Ccp=1.6，Ckleb=0.3是基于跨声速的平衡流动得出的，并不适用于超声速及高超声速的复杂流动;另一方面外层涡粘性的捕捉严重依赖于Fmax，Ymax的确定，原始的BL模型并未限制寻找Fmax的范围，在复杂流动中会导致长度尺度 Ymax的不确定性.图1为采用两方程Wilcox k-ω模型对24°超声速压缩拐角数值计算结果，可看出即使在附体流动（图2站位x=－1），由于剧烈的非平衡效应，F在边界层外存在一个虚假的极大值，在分离区及激波区域（图2 站位 x=－0.5，－0.3，0，0.3，0.5），出现多个极值，不同极值间相差近一个量级.显然在复杂流动中，原始的BL模型将沿流向得到非物理或间断的Fmax与 Ymax，从而导致涡粘性分布不均匀，使得BL模型的应用受到限制.

针对上述问题，本文提出熵限制的概念.熵的大小表征能量的耗散程度，由于边界层内湍流剧烈的脉动以及与壁面的摩擦作用，当地的熵值要远远大于外流，同时研究发现，在超声速流动中，无论是在流动附体区还是激波/边界层干扰的分离区，沿壁面法向熵值都能够保持较好的单调性（图3）.因此，本文以熵的大小作为函数F搜寻范围的判断指标，进而保证涡粘性的合理分布.

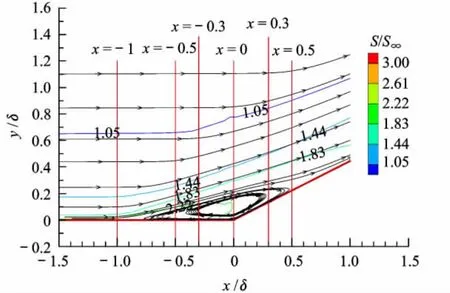
图1 24°压缩拐角等熵线图，Ma=2.84

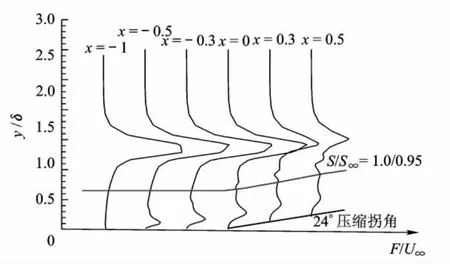
图2 函数F沿壁面法向分布图

搜寻过程分两步完成:①沿壁面法向向外搜索直到S/S∞＞C停止，储存停止位置;②函数F由停止位置反向搜索，确定 Fmax与 Ymax，如图 4所示.

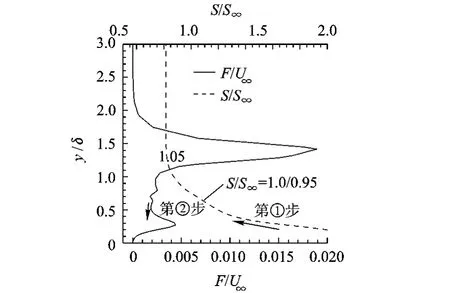
图4 搜寻过程示意图

本文中常数C比拟边界层厚度δ:Ue/U∞=0.95，取 C=1.0/0.95.修正后模型采用文献［4］针对超声速流动建议的Ccp=2.08.

2 计算结果及分析

本文采用 BL-origin、BL-entropy以及两方程k-ω模型分别对超声速平板（Ma=2.25）、超声速压缩拐角（Ma=2.85）、超声速膨胀-压缩拐角（Ma=2.9）进行数值模拟，流动现象包括简单的附体流动到复杂的激波/边界层干扰、分离以及再附，以期对这种新型的修正方式进行综合的评估.

2.1 超声速平板算例

文献［7］采用DNS方法对超声速平板进行数值试验，试验条件如下:Ma∞=2.25，Re=63500 in－1（1 in=2.54 cm）.

如图5所示，将BL-origin模型中的Ccp改为2.08，构造 BL-origin-coe，计算结果与 BL-entropy重合，但在对数率区与BL-origin差别较大，一方面说明对于简单的平板流动，本文提出的熵限制修正能够回归到原始模型，另一方面再次印证模型参数（Ccp，Ckleb）对BL模型性能有较大的影响.鉴于超声速可压缩效应的影响，4种模型计算结果与DNS数据稍有差异.

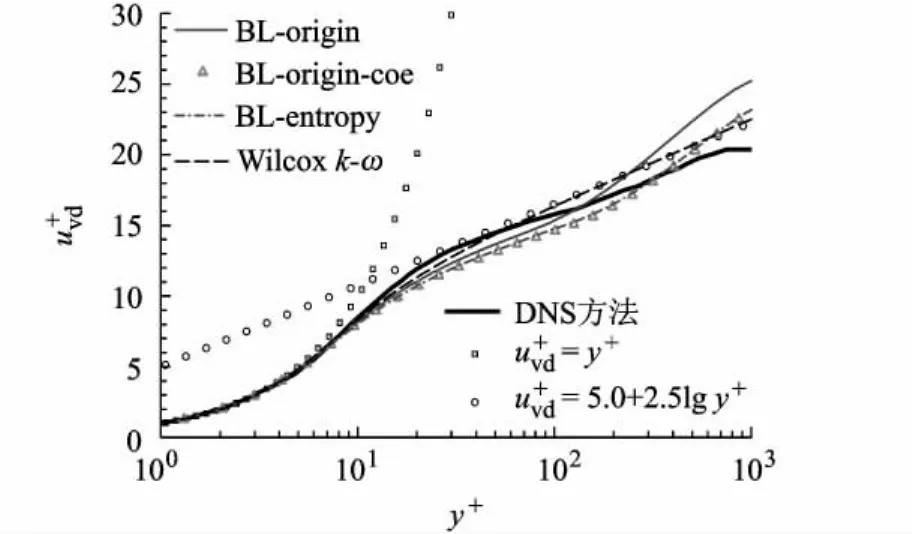
图5 超声速平板速度型（x=8.8 in）

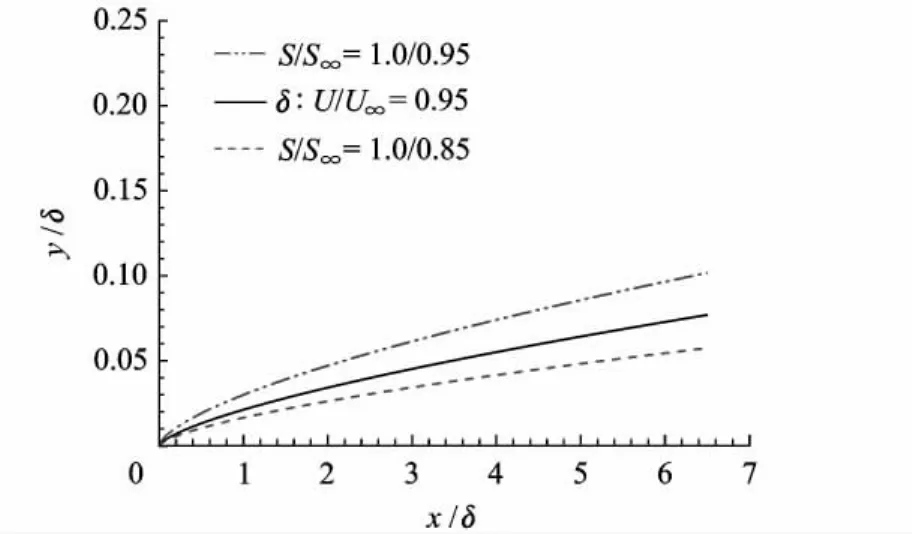
图6 平板边界层以及等熵层

图6为沿流向（x方向）平板边界层厚度以及等熵线位置分布，可以看出等熵线具有类似边界层的性质，文中选取C=1.0/0.95既能将边界层包络在内，又能将外流分割出来，对函数F的搜寻范围起到合理的约束作用.

2.2 超声速压缩拐角

文献［8］在普林斯顿大学超声速风洞对二维压缩拐角进行了试验研究，其中24°压缩拐角试验条件如表1所示.

表1 24°超声速压缩拐角试验条件

如图7所示，超声速气流流至拐角前段时，在逆压梯度的作用下，边界层变厚，从而使主流提前产生一系列的压缩波，并在离拐角一定距离处汇聚成一道分离激波，激波后边界层往往不能承受强逆压梯度而发生分离，形成一个“凸包”，超声速气流流经该“凸包”后紧接着在斜面的压缩作用下，形成新的压缩波区.

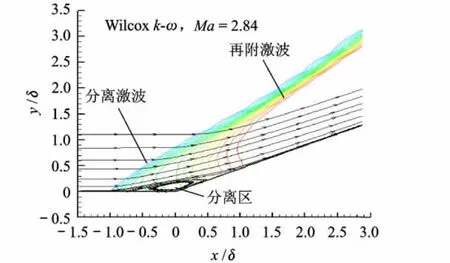
图7 超声速压缩拐角流场示意图

与文献［9－10］结论一致，本文采用BL-origin进行计算未能得到收敛结果.图8为修正后的BL-entropy与Wilcox k-ω计算所得壁面压力、摩擦力分布，可以看出，BL-entropy能够很好地预测分离点的位置，其中压力分布与试验值吻合一致，但再附区中涡粘性预估不足，导致摩擦力低于试验值.对比两个模型计算所得涡粘性分布（图9），BL-entropy能够有效地将涡粘性均匀地限制在壁面附近，达到了熵限制的目的.

2.3 超声速膨胀-压缩拐角

超声速湍流膨胀-压缩拐角是吸气式高超声速飞行器燃烧室和尾喷管部分的典型流动.采用的试验模型来流条件为［11－12］:拐角角度 α =25°，高度 h=15 mm，Ma=2.9，单位长度雷诺数 Re=3.8×107m－1，来流湍流边界层厚度在膨胀拐点处为δ=5.08 mm.

图10为超声速膨胀-压缩拐角流场示意图，超声速气流在第一个拐角处发散出膨胀波系，在压缩拐点处由于强逆压梯度形成分离区，分离区前后分别为分离激波和压缩激波，两道激波在下游交汇.

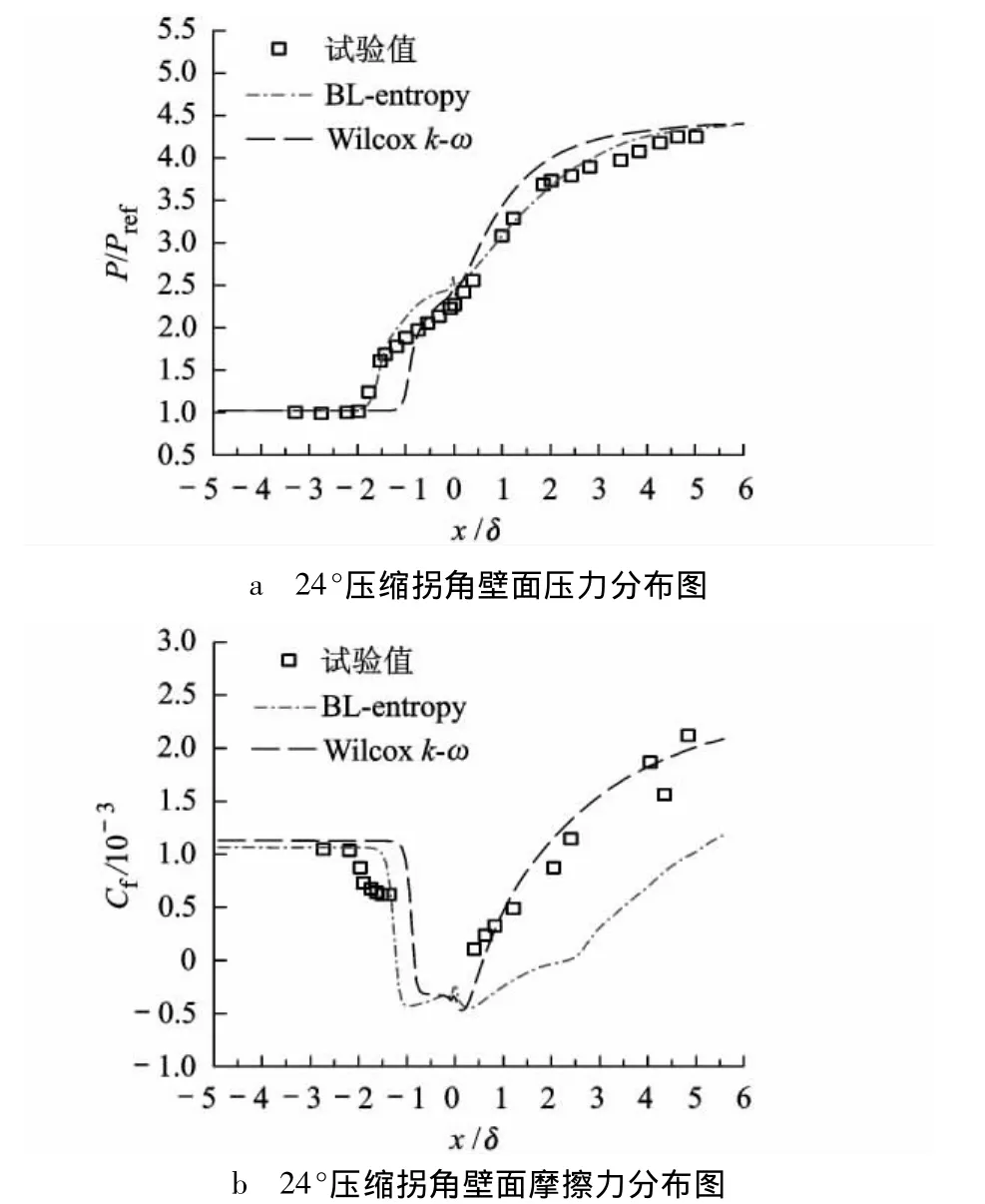
图8 压缩拐角壁面压力与摩擦力分布图

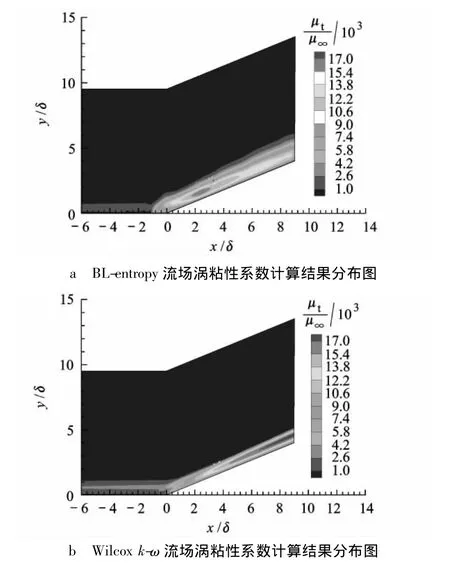
图9 压缩拐角流场涡粘性系数分布图

图11、图12分别为3个模型计算所得压力、摩擦力以及涡粘性分布图.

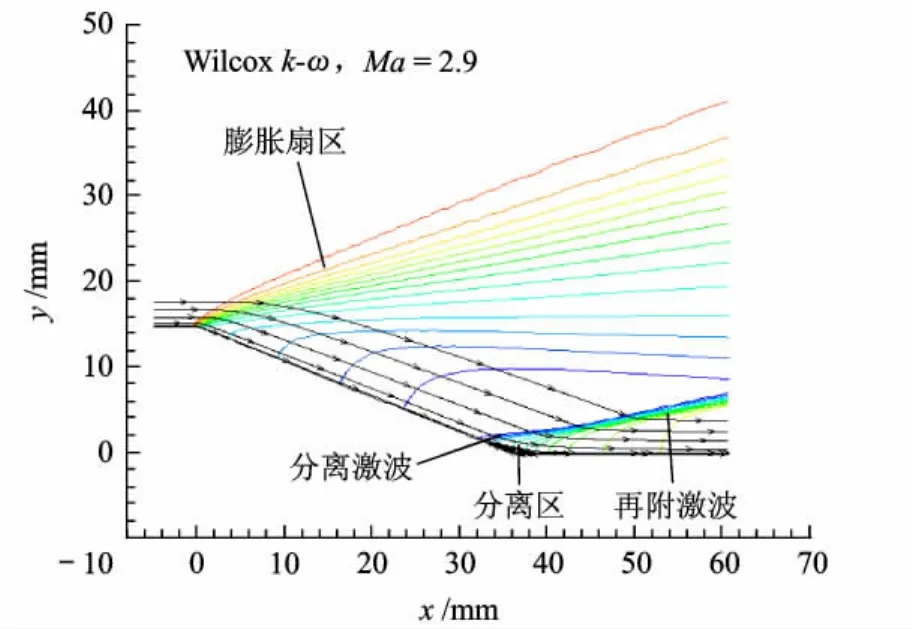
图10 超声速膨胀-压缩拐角流场示意图

可以看出，BL-entropy极大地改进了 BL-origin的性能.BL-entropy与Wilcox k-ω压力计算结果一致且与试验值吻合良好，在再附点处摩擦力计算结果偏低，其他区域与试验值一致.BL-origin由于在分离区无法确定合理的长度尺度 Ymax，导致压力与摩擦力计算结果在分离区域出现“震荡”，并且由图12可以看出，BL-origin计算所得涡粘性在整个膨胀扇区以及分离区出现间断，导致分离区过大.BL-entropy在膨胀扇区涡粘性计算偏小，其他区域与Wilcox k-ω计算结果相近，说明本文提出的熵限制的方法能够克服原始模型的缺陷，更好地符合物理本质.

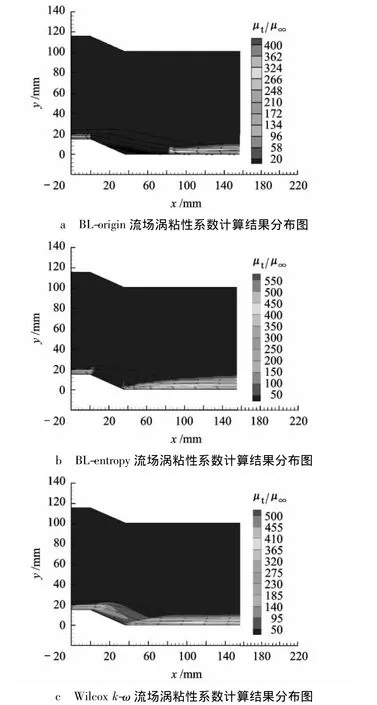
图12 膨胀-压缩拐角流场涡粘性系数分布图

3 结论

BL-origin模型由于未限制长度尺度的搜索范围，使其在模拟激波/边界层干扰、分离、再附等复杂流动时无法获取正确的涡粘性分布，从而导致计算发散或者得出错误流场.本文针对上述不足，提出一种基于熵限制的新型修正方式.熵是衡量能量耗散的指标，超声速流动中壁面处的熵值远远大于外部流动，同时，熵值在复杂流动区域也能够保持较好的单调性.本文利用熵的上述特点，在原始的BL模型中引入熵限制，通过对超声速平板、超声速压缩拐角、超声速膨胀-压缩拐角3种典型算例进行计算研究，得出以下结论:

1）BL模型中的参数Ccp，Ckleb与马赫数有关，并直接影响BL模型的性能;

2）对于激波/边界层干扰、分离、再附区域，原始的BL模型不能正确捕捉涡粘性，会造成预测分离点提前，分离区过大甚至导致流场计算发散的问题;

3）采用熵限制后的BL模型能够获得符合物理意义的涡粘性分布，在再附点区域涡粘性偏小，需要进一步改进;

4）本文提出的新型熵限制方式保持了BL-origin模型的简单、效率高的优势，其思想可以推广到其他与超声速边界层相关的模型当中.

（References）

［1］Baldwin B S，Lomax H.Thin layer approximation and algebraic model for seperated turbulent flows［R］.AIAA-78-257，1978

［2］Degani D，Schiff L B.Computation of supersonic viscous flows around pointed bodiesatlargeincidence［R］.AIAA-83-0034，1983

［3］Panaras A G，Steger J L.A thin-layer solution of the flow about a prolate spheroid［J］.Z Flugwiss，1988（12）:173－180

［4］Panaras A G.Algebraic turbulence modeling for swept shockwave/turbulent boundary-layer interactions［J］.AIAA Journal，1997，35（2）:456－463

［5］Shang J S，Hankey W L，Jr.Numerical solution for supersonic turbulent flow over a compression ramp［J］.AIAA Journal，1975，13（10）:1368－1374

［6］Wilcox D C.Reassessment of the scale determining equation for advanced turbulence models［J］.AIAA Journal，1988，26（11）:1299－1310

［7］Gao H，Fu D X，Ma Y W，et al.Direct numerical simulation of supersonic turbulent boundary layer flow［J］.Chinese Physics Letters，2005，22（7）:1709－1712

［8］Settles G S，Dodson L J.Hypersonic shock/boundary-layer interaction database［R］.NASA-CR-177577，1991

［9］Visbal M，Knight D.The Baldwin-Lomax turbulence model for two-dimensional shock-wave/boundary-layer Interactions［J］.AIAA Journal，1984，22（7）:921－928

［10］Forsythe R，Hoffmann A，Damevin M.An assessment of several turbulence models for supersonic compression ramp flow［R］.AIAA 98-2648，1998

［11］Knight D.RTO WG 10:test cases for CFD validation of hypersonic flight［R］.AIAA 2002-0433，2002

［12］Knight D，ran H，Panaras A，et al.RTO WG 10:CFD validation for shock wave turbulent boundary layer interactions［R］.AIAA 2002-0437，2002

New kind Baldwin-Lomax turbulence model under the limit of entropy

Zhao RuiYan Chao Yu Jian
（School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

A new kind correction to Baldwin-Lomax turbulence model（BL-entropy）based on the concept of entropy was proposed. The supersonic plane， two-dimensional supersonic compression corner and expansion-compression corner which were representative in the engineering area were chosen in the numerical simulation to evaluate the performance of this model.It is found that BL-entropy can conquer the essential deficiency of the original model by providing a more physically correct length scale in the supersonic complex flow.Moreover，this method is simple，computationally fast and general，making it applicable to other models related with the supersonic boundary layer.

turbulence models;entropy;supersonic flows;computational fluid dynamics

V 211.3

A

1001-5965（2012）02-0175-05

2010-11-12;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:47;

CNKI:11-2625/V.20120221.1147.029

www.cnki.net/kcms/detail/11.2625.V.20120221.1147.029.html

国家973计划资助项目（2009CB724104）

赵 瑞（1987－），男，山东阳谷人，博士生，zr8800@126.com.

（编 辑:李 晶）