高超声速飞行器刚体/弹性体耦合动力学建模

李惠峰 肖 进 张 冉

（北京航空航天大学 宇航学院，北京 100191）

高超声速飞行器刚体/弹性体耦合动力学建模

李惠峰 肖 进 张 冉

（北京航空航天大学 宇航学院，北京 100191）

高超声速飞行器广泛采用升力体、乘波体等气动布局和轻质复合材料、薄壁结构等，导致结构振动与刚体运动频率非常接近，给飞行器制导控制系统设计带来了巨大挑战.针对该类飞行器的特点，考虑结构的横向位移，将机身前后体简化为于质心处固联的2根悬臂梁，并从统一的能量观点出发，基于拉格朗日方程与虚功原理，在纵向平面推导出适合高超声速飞行器的刚体/弹性体耦合动力学模型.通过对比耦合模型与传统刚体模型的极点分布情况，发现结构振动与刚体短周期模态紧密耦合，离心力的引入影响了高度与长周期模态，对高超声速飞行器航迹运动的作用不可忽视.最后分析了飞行速度与结构阻尼变化对耦合模型动态性能的影响.结果证明飞行速度对刚体运动模态影响显著，而结构阻尼的变化主要改变弹性模态.

高超声速;耦合模型;结构振动;拉格朗日方程

随着高超声速飞行器的出现，为节省燃料广泛采用轻质的复合材料，设计细长体、升力体等气动布局，这些因素导致结构固有振动频率的降低，于是必须考虑刚体和弹性体的惯性耦合现象［1］.特别是以吸气式超燃冲压发动机为动力的X-43和X-51，发动机对飞行条件以及气动外形提出的要求非常苛刻，在高马赫数下机体的弹性振动直接影响到激波角，进而改变了发动机的进气情况.

以协和号超音速客机为例首次提出刚体与弹性振动的耦合建模［2］，但是耦合仅体现在定常与非定常气动力的相互影响.在此基础上，文献［3］推导出刚体/弹性体的动力学耦合一般模型，称为强耦合真实模型（TMH，Truth Model with Heave coupling）.但TMH中未考虑高马赫数下地球离心力对飞行器运动的影响，且未将推力加入到机体轴向的非保守力系，不能真实地体现高超声速飞行器的特点.文献［4］将TMH中相对较弱的耦合项去掉，得到基于控制的简化模型（TM，Truth Model）.文献［5］将尖头体高超声速飞行器机体前缘的结构振动速度与攻角状态线性叠加，主要是为了验证结构振动对发动机进气的影响，但其忽略了对其他飞行状态量的影响以及刚体运动对结构振动的反作用.为了更真实地体现飞行器结构振动模态，文献［6］将机身简化为一根自由-自由梁，取前三阶固有振型，结果显示惯性耦合项系数为零，无法体现出结构与刚体运动的强耦合现象.综上所述，国外已进行过耦合建模的相关研究，但研究对象及内容各有不同.由于我国在高超声速飞行器的理论研究和实际应用方面相对落后，本文研究目的是在充分借鉴国外公开发表的文献资料基础上，结合吸气式高超声速飞行器的特点，推导出较真实的动力学耦合模型，以便为未来针对该类型飞行器的先进制导和控制系统理论研究和仿真验证以及进行结构/制导控制一体化设计打下良好基础.

本文首先建立机体的结构振动模型，将机体简化为2根于质心处固连的悬臂梁，分别求出前四阶的固有振型和自然振动频率;然后建立刚体/弹性体的耦合矢量模型，结合吸气式高超声速飞行器的特点，基于拉格朗日方程推导出耦合动力学模型;最后通过将耦合非线性模型线性化，求取平衡点，并在此基础上分析极点分布情况，总结了结构振动与刚体运动的耦合原因以及离心力、飞行速度与结构阻尼对耦合模型动态性能的影响.

1 机身振动简化模型

在飞行器设计的初级分析阶段，为了减少仿真计算量的同时又不失真实性，通常将全机振动模型简化为弹性梁.本文以类X-43A飞行器为研究对象，由于此飞行器长度远大于厚度，机身近似细长体，并考虑到推进系统对前体激波的形成与后体外膨胀段的外形要求，机体设计成中间粗、两端细，容积和大部分质量集中于质心周围.因此，将机身前体和后体分别简化为悬臂梁，于质心处固连，是较合理的假设，并且能体现出刚体与弹性体之间的强耦合［5］.

结构的变形分为横向、轴向位移与扭转变形，为简化起见，本文只研究变形最明显的横向位移.

基于以上假设，振动位移w（x，t）与机体轴向坐标和时间有关，由梁的弯曲理论，无阻尼自然振动方程如下:

以前体悬臂梁为例，通过分离变量法，并结合边界条件可求出结构固有振型φ与自然振动频率ω的解析解:

其中，i为振型的阶数.

图1是机体前悬臂梁的前四阶振型，此振型值体现在下文中建立的刚体/弹性体惯性耦合项系数中.

对应的自然振动频率分别为

通常，固有频率越低，与刚体运动频率越接近，故耦合越严重，本文对于前后体悬臂梁均取第1阶振型与固有振动频率.

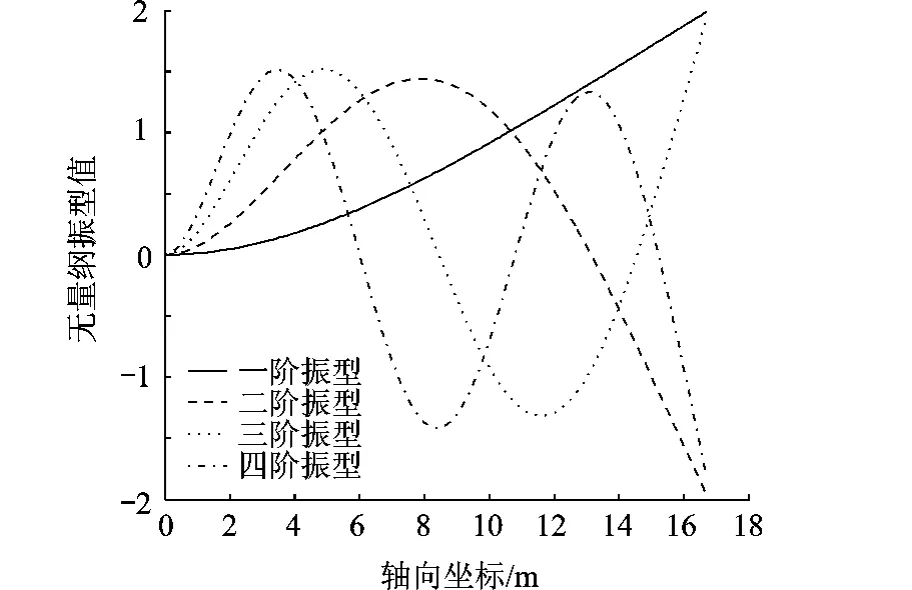
图1 机身前端简化悬臂梁前四阶振型

2 刚体/弹性体矢量模型建立

刚体/弹性体耦合建模的重点在于矢量模型的建立.不同于以往刚体假设的是，真实弹性体飞行器上各点与质心的距离不是一成不变的，而是在其附近存在着微幅振动.本文假设只存在结构的横向位移，而忽略影响较小的轴向位移.矢量模型如图2所示.

假设rO为从惯性系原点On指向机体系原点（质心）O的矢量，如图2，向量之间存在关系:

其中，O为飞行器质心;P为刚体飞行器纵向平面上任一点.现假设该飞行器伴随有结构弹性振动位移:

其中，ηz，i为第 i阶结构横向位移变量.

ρ=xxb+zzb表示刚体模型上P点相对于O点的位移矢量，所以有rP/O=d+ρ.于是，式（4）可变成 rP=rO+d+ρ.

图2 结构振动/刚体运动耦合矢量模型

P点的速度矢量:

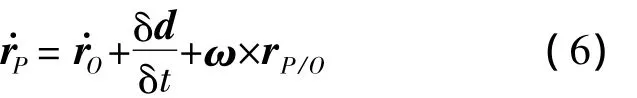
在纵向平面内，惯性系与机体系存在如下转换关系:

其中，θ为俯仰角.

将惯性系下的质心矢量投影到机体系下得

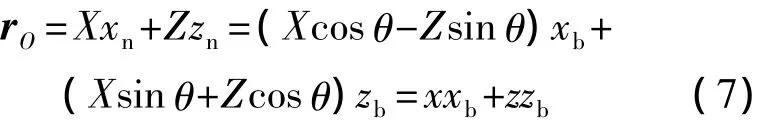
于是，有

得到机体系下质心的速度矢量为

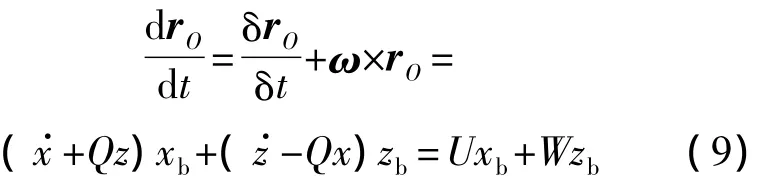
其中，U，W分别为飞行速度沿机体轴 xb，zb的分量.

3 刚体/弹性体耦合动力学模型

结合以上的矢量定义，将整个飞行器视为多质点系，只考虑纵向平面的位移，并利用振型的正交性可求出总动能如下:

其中，Iyy为惯性矩;λz，i，ψxz，i为惯性耦合项系数.

总势能为重力势能与弹性势能之和，即

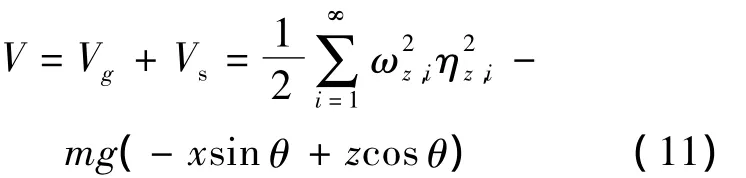
其中，m 为飞行器质量;ωz，i为结构第 i阶自然振动频率.

根据虚功原理:

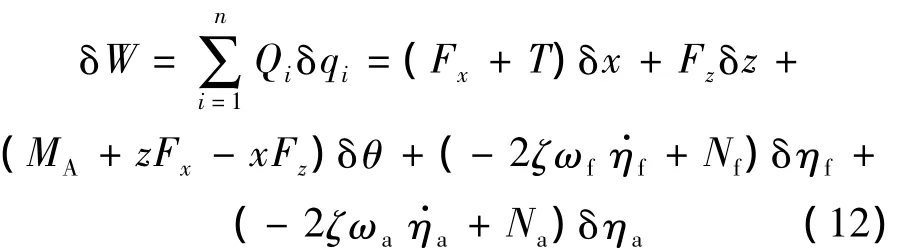
式中，下标f，a分别代表飞行器前体与后体;T为发动机推力;－2ζωη·为结构振动的阻尼力，ζ为结构振动阻尼;N为引起结构振动的载荷力;Fx，Fz分别为机体系下沿机体轴向和法向的合力;MA为俯仰力矩.通过机体系与气流系的坐标转换，可得到升力（L）和阻力（D）的表达式:

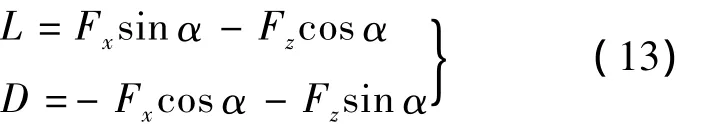
结合拉格朗日函数和虚功表达式进行拉格朗日方程求解，可推导出高超声速飞行器刚体/弹性体耦合的动力学方程组:

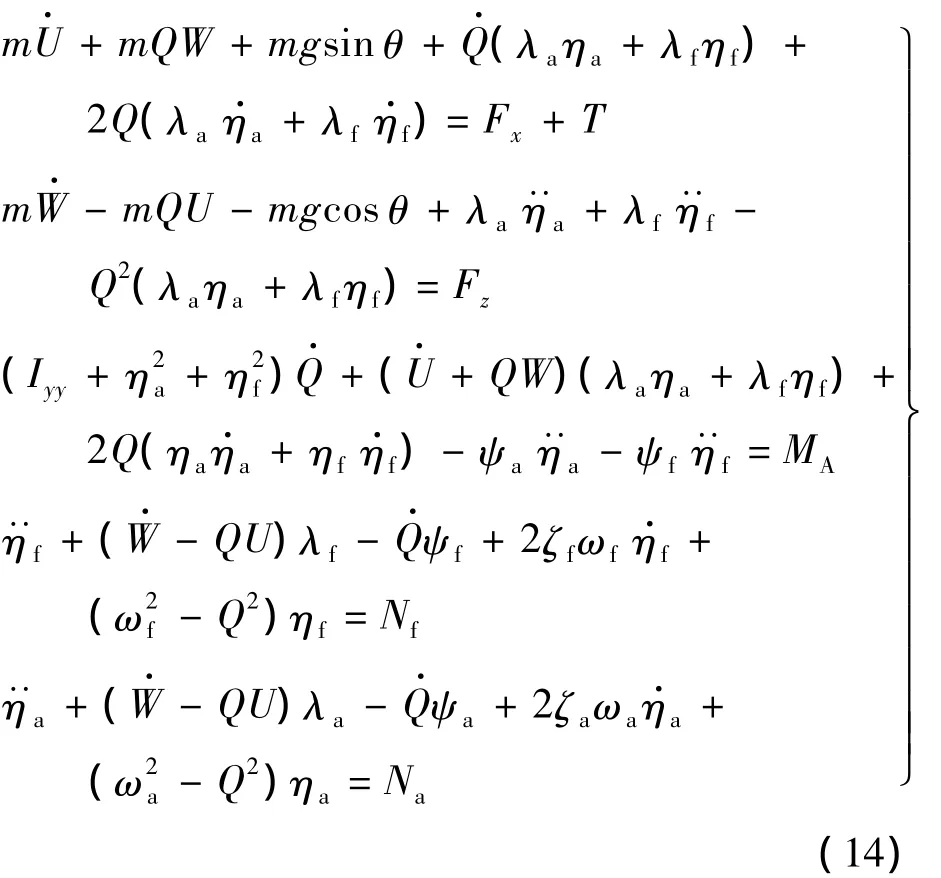
式中，惯性耦合项系数求解如下:

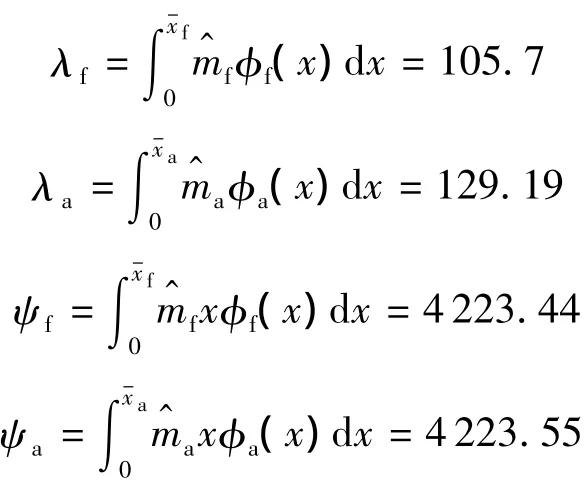
以上是机体系下的动力学方程，通常所需的状态量攻角（α）和速度（V）由下式表示:

通常情况下，低速飞行器的重力加速度求解只与高度有关，但对于高超声速飞行器，还必须考虑离心力对其的影响，所以经简化的重力加速度求解公式为

其中，G为万有引力常数;M为地球质量;r为从地心到飞行器质心的距离.

由于本文只在纵向平面建模，即假定横侧向状态量均为0，使得与之相关的哥氏力在纵向平面的投影亦为0.并且，在高马赫数下哥氏力相对于离心力为小量，因此，建模中只考虑离心力对耦合模型的作用.

4 模型分析

基于以上耦合模型，参考文献［4］中的气动力模型及相关结构、外形参数如下:

使用MATLAB中trim函数在固定高度与速度下求取平衡工作点，见表1.其中2个控制输入:发动机节流阀值β和俯仰舵偏角δe.

由表1数据可看出，攻角越大，发动机节流阀值越小，即省燃料;而结构振动幅值却与之成正比，当进行攻角优化时需折中考虑.

4.1 耦合模态分析

本文在高度为25 908 m，马赫数为8平衡点下将耦合模型线性化并求解其特征根，同时，为了体现出其特点，求出了相同条件下纯刚体运动模型的极点分布，以便对比.表2为耦合模型与刚体模型的极点分布情况.

表1 不同高度与速度下的平衡点

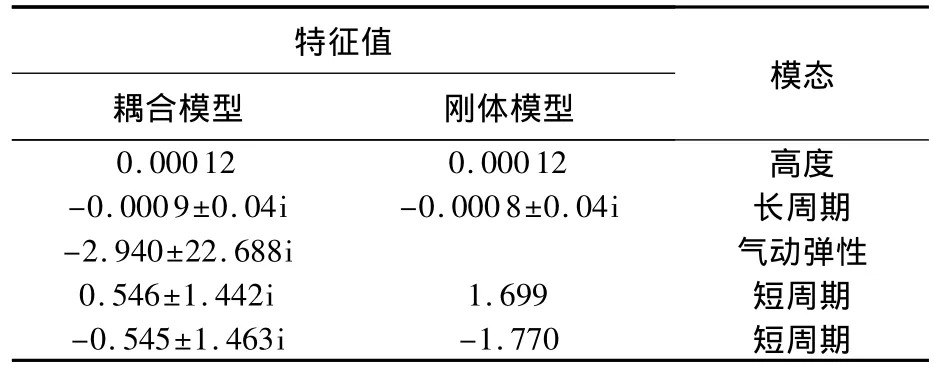
表2 极点分布对比

通过分析表2的数据，可得出以下结论:

1）与经典刚体模型不同，耦合模型由于加入了2个弹性振动方程，总共出现9个特征根，可分为高度模态、长周期模态、短周期模态和一对稳定的气动弹性模态.各运动参数随时间的变化是上述4种模态的叠加.

2）与刚体模型的极点分布情况相比，二者的高度模态和长周期模态非常接近，说明巡航飞行中结构振动对高度、速度和航迹倾角的影响很小.但由于引入了结构振动，刚体运动的2个短周期实根变成了2对共轭复根，说明由于结构的振动导致了攻角和俯仰角速度的震荡现象，同时结构的振动模态与短周期模态产生了耦合.由此可知，该耦合模型主要改变了刚体运动的短周期模态，同时，攻角等短周期状态量的改变也严重影响了结构的振动特性.

由图3所示，在相同平衡点处将耦合模型线性化，求出极点分布，并与完全去除惯性耦合项的模型极点分布对比.容易看出，除了代表高度模态和长周期模态的中间3点基本重合，其余极点位置相距较远，形象地表示出刚体/弹性体耦合运动模型中各模态的强耦合现象.

图3 耦合/解耦模型极点分布对比

4.2 离心力对模态的影响

表3分别给出了耦合模型中有无离心力的极点分布情况.

表3 离心力对极点分布的影响

从表3中数据能看出，离心力对高度模态的影响最大，达到97.8%，直观上说是减缓了高度状态量的发散速度，其次是长周期模态3.3%，而对短周期模态和气动弹性模态的影响可以忽略.由此得知，虽然离心力对姿态状态量与结构振动的影响非常小，在控制器设计时可以不予考虑，但是对于高超声速刚体/弹性体耦合模型的制导控制一体化设计时不能简单省略.

4.3 参数变化对模态的影响

由图4可见，在同一高度下，飞行马赫数从8变化到10的过程中，短周期的2对共轭复根逐渐向虚轴靠拢，说明姿态角状态量的衰减速率随着马赫数的增大而减小，且趋于临界稳定;当速度继续增大，其振荡频率随之升高.从以上推导的耦合动力学方程中也能看出，马赫数的变化对飞行姿态和弹性振动的影响非常明显.

图4 速度变化对模态的影响

图5 结构阻尼对模态的影响

如图5所示，当结构阻尼从0.1～0.7变化时气动弹性模态的衰减速度加快、振动频率明显降低，而对其它模态的影响相对较小.

5 结论

本文基于拉格朗日方程与虚功原理推导了高超声速飞行器的刚体/弹性体耦合动力学模型，分析得到如下结论:

1）结构振动与刚体短周期模态的相互影响非常明显，对该类型飞行器控制系统设计时需要着重考虑;

2）离心力的引入主要改变了高度和长周期模态，使得高度模态的发散速度减慢;

3）随着飞行速度的增加，各极点值向零靠拢，整个系统趋于临界稳定，结构阻尼的变化主要影响弹性模态.该模型能真实地反映高速飞行器的运动特性，体现出了强耦合、强非线性的特点.

需要说明的是，本文主要考虑减少计算量的同时方便分析该模型，因此，结构载荷力中未引入因结构振动产生的非定常气动力，但在实际工程应用中高马赫数下的非定常气动力不可忽视，这部分工作可在以后开展.

（References）

［1］杨超，许赟，谢长川.高超声速飞行器气动弹性力学研究综述［J］.航空学报，2010，31（1）:1－11

Yang Chao，Xu Yun，Xie Changchuan.Review of studies on aeroelasticity of hypersonic vehicles［J］.ACTA Aeronautica et Astronautica sinica，2010，31（1）:1－11（in Chinese）

［2］Waszak M R，Schmit D K.On the flight dynamics of aeroelastic vehicles［R］.AIAA-1986-2077-388，1986

［3］Bolender M A，Doman D B.A non-linear model for the longitudinal dynamics of a hypersonic air-breathing vehicle［R］.AIAA-2005-6255，2005

［4］Parker J T，Bolender M A，Doman D B.Control-oriented modeling of an air-breathing hypersonic vehicle［R］.AIAA-27830-611，2007

［5］Clark A D，Mirmirani M D，et al.An aero-propulsion integrated elastic model of a generic air-breathing hypersonic vehicle［R］.AIAA-2006-6560，2006

［6］Rodriguez A A，Dickeson J J，Sridharan S，et al.Control relevant modeling，analysis，and design for scramjet-powered hypersonic vehicles［R］.AIAA-2009-7287-980，2009

Hypersonic vehicle rigid/elastic coupled dynamic modeling

Li Huifeng Xiao Jin Zhang Ran
（School of Astronautics，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

Extensive use of lifting body，wave-rider aerodynamic layout and other composite materials，thin-walled structures，lead the frequency of structural vibration and rigid body motion very close.This yields a great challenge to the vehicle control system design.Taking into account the transverse displacement，a specific simplification which treats the vehicle body as two mass center fixed cantilever beams was adopted.And the hypersonic aircraft's rigid body/elastic coupling model was derived based on the principle of virtual work and Lagrange equations.After comparing the open-looped poles of new coupling model and traditional rigid body model，a conclusion that the short-period vibration mode and the structures vibration mode tightly coupled with each other was made.The centrifugal force affected the height and long-period mode，and the effect on the flight path can not be ignored.Finally，changes in flight speed and structural damping on the dynamic performance of coupled model were analyzed.Results show that flight speeds significantly affect the rigid body motion modes，while the structural damping mainly changes in elastic mode.

hypersonic;coupling model;structure vibration;Lagrange equation

V 212.1

A

1001-5965（2012）02-0160-06

2010-10-14;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:46;

CNKI:11-2625/V.20120221.1146.010

www.cnki.net/kcms/detail/11.2625.V.20120221.1146.010.html

李惠峰（1970－），女，陕西蒲城人，副教授，lihuifeng@buaa.edu.cn.

（编 辑:赵海容）