基于集对分析的区域公交化旅客运输换乘设施布局方案优选

鲍陈希 上海铁路局上海站

在区域公交化旅客运输换乘设施布局方案的优选中，并不能对所有的评价指标进行准确定量的描述，总是存在一些具有相互交错性和不确定性的定性指标。因此，本文基于集对分析原理，综合考虑确定性因素和不确定性因素，对区域公交化旅客运输换乘设施布局的多方案进行比较，选出最优方案，并通过算例进行验证。

1 基于集对分析的多方案评价方法

集对分析理论是我国学者赵克勤先生提出的一种处理不确定问题的系统分析方法。该理论把系统的不确定性称为“差异”，把确定性划分为“同一”和“对立”。其基本思想是在一定的背景下，对组成集对的两个集合特性做同一性、差异性和对立性的分析，并建立两个集合的同、反、异联系度表达式，从相互联系、相互制约、在一定条件下可以相互转化的同、反、异这三个方面对事物及其系统进行分析。集对分析具有信息全面、概念清晰和计算简便的优点。

设某问题 A 有A1，A2，…，Am共 m 个方案，每一方案有f1，f2，…，fn共n个指标。各指标的量纲可以相同，也可以不同，每个指标都有1个值，记为fij（i=l，2，…，m；j=l，2，…，n），表示第 i个方案的第j个指标的值，且有

1.1 构建同一度决策矩阵

首先建立多方案评价决策矩阵H：

这些指标中，有些指标属于成本型指标，指标值以最小为最优；有些指标属于效益型指标，指标值以最大为最优。取m个方案中各指标的最优值组成理想方案A0，即A0=（f01，f02，…，f0n）。其中，成本型指标f0j=min（fij），效益型指标f0j=max（fij），i=l，2，…，m；j=l，2，…，n。

计算被评价方案Ai（i=l，2，…，m）的各指标值fij与理想方案A0的各指标值f0j的同一度aij，即aij=fij/f0j（i=l，2，…，m；j=l，2，…，n） 。

由此组成各被评价方案指标与理想方案指标基于集对分析的不带权的同一度矩阵Q，即

1.2 确定各评价指标的权重

由于换乘衔接设施布局评价的复杂性，呈现出多层次结构，因此采用层次分析法进行研究。经过专家打分、计算，得到判断矩阵B、判断矩阵特征向量W。

1.3 建立综合评价模型

确定被评价方案Ai与理想方案A0的带权同一度矩阵R，即R=WTQ。R的元素ai（i=l，2，…，m）就是被评价方案i与理想方案的带权同一度的和，即

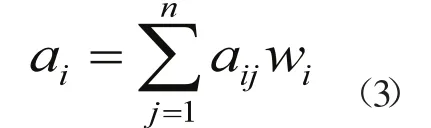
ai的大小排序即为各被评价方案的优劣排序，ai最大者就是最优方案。

2 区域公交化旅客运输换乘设施布局评价指标体系的建立

本文选择“目标—准则—指标”层次结构模式，建立区域公交化旅客运输换乘设施布局方案的评价指标体系，形成有序的递阶层次结构。换乘设施布局的评价涉及诸多内容，本文仅从各种衔接交通方式的协调运行出发，从换乘效率、换乘舒适性和经济及环境三个方面考虑，相应地提出换乘走行距离、换乘走行时间、运能匹配度、换乘安全性、换乘设施舒适性、投资额、用地规模及对环境影响等10个指标，建立评价指标体系如图1所示。

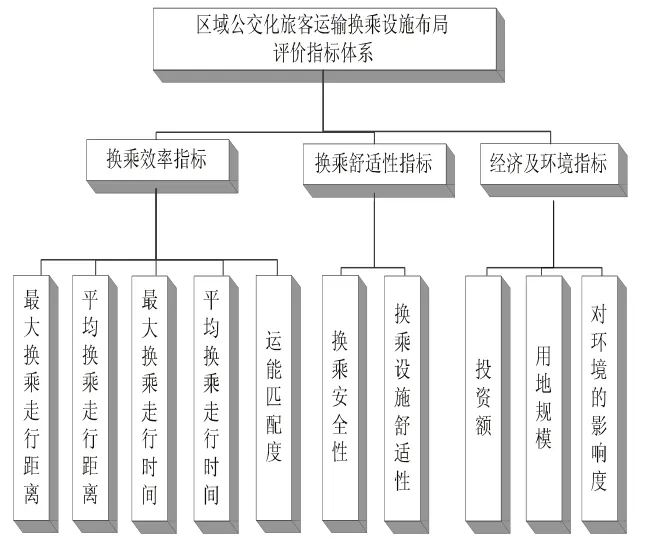
图1区域公交化旅客运输换乘设施布局评价指标体系

2.1 换乘效率指标

（1）最大换乘距离Smax：是指布局方案中，各种衔接交通方式与铁路间换乘旅客的最远换乘距离，即Smax=max{Si}。其中，Si表示第i种衔接交通方式站场与铁路车站的距离，i=1，2，…，n。

（2）平均换乘距离Savg：是指布局方案中，所有衔接交通方式与铁路间换乘旅客的换乘距离的平均值，即：

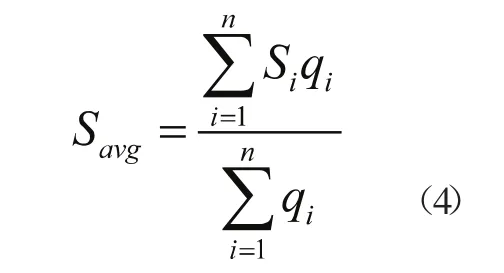
其中，qi表示第i种衔接交通方式与铁路间的换乘旅客人数。

（3）最大换乘时间Tmax：根据 G·布莱顿假设，步行距离和感到舒适的步行时间的函数关系为：T=K·Drr。其中，T为换乘步行时间（min），D为换乘步行距离（km），K、r为系数。考虑到换乘客流特征，可将G·布莱顿假设标定为：T=40.77D1.44，则最大换乘时间Tmax=max{ti}。

其中，ti为第i种衔接交通方式到铁路车站的换乘时间。

（4）平均换乘时间Tavg

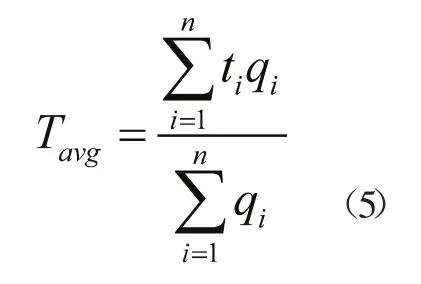
符号意义同前。

（5）运能匹配度B：指的是衔接交通方式与铁路的运输能力的匹配协同情况，可用铁路列车密集到达期内各衔接交通方式客流量与该交通方式运输能力的比值来衡量，即：

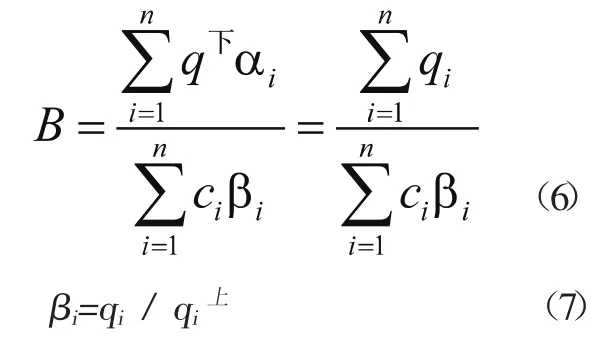
其中，q下为铁路在密集到达期的下客量（人次／h），ai为其中换乘衔接交通方式i的旅客所占总下客量的比例，ci为衔接交通方式 i的运输能力（人次／h），βi为铁路换乘衔接交通方式i的客流占该交通方式上客量的比例（%），qi为铁路换乘衔接交通方式i的客流量，qi上为衔接交通方式i总的上客量。

2.2 换乘舒适性指标

（1）换乘安全性

换乘安全性包括换乘客流与其他交通流线交叉干扰程度，以及为保证旅客换乘安全而设置的隔离设施、消防设备、紧急疏散通道等的有效度。换乘安全性很难用科学、准确的计算公式作出完整的描述，可以请专家进行评估打分。

（2）换乘设施舒适性

换乘舒适性指的是换乘客流从信息引导标志、通道设置等各项设备设施中获取服务的舒适程度。该指标反映的是换乘过程中旅客的心理感受，也属于定性指标，可以用专家打分法或旅客调查问卷对其进行评估。

2.3 经济及环境指标

（1）投资额Mall：指的是为兴建该布局方案各项设备设施所花费的全部费用，可用各设计方案的投资估算来衡量。

其中，Mi是第i种衔接交通方式设施投资额。

（2）用地规模Aall：土地是不可再生资源，因此希望布局方案能完成既定集散换乘目标的同时减少用地规模Aall。

其中，Ai为第i种衔接交通方式站场用地面积。

（3）对环境的影响度。

主要指建设前期引起的拆迁量、建设过程中对周围交通的影响及建成投入使用后对城市造成的分割。这一指标涵盖的内容较多且具有不确定性，属于定性指标，可通过专家打分来赋予评价值。

3 算例分析

R市新建铁路客运车站选址已定，规划中与其衔接的公共交通方式有城市轨道交通和常规公交两种。现有三个布局方案：

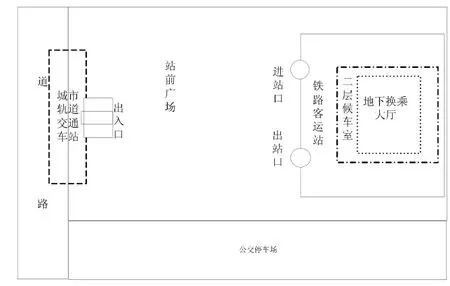
图2换乘衔接设施布局方案A

方案A：城市轨道交通线路布置在铁路客运站站前广场地下，在广场设进出口；在站前广场外设公交停车场。

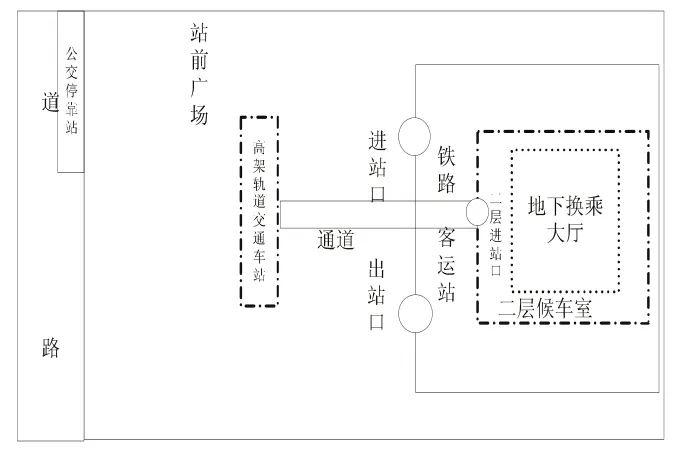
图3换乘衔接设施布局方案B

方案B：城市轨道交通线路高架设置，与铁路车站候车室有通道直接相连；在站前广场前道路旁设公交车站。

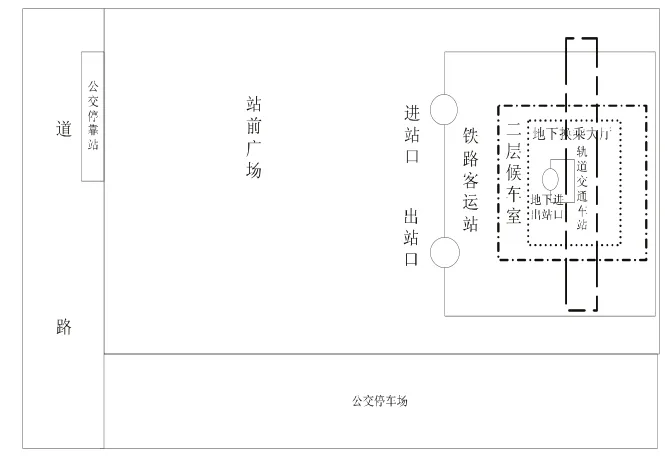
图4换乘衔接设施布局方案C

方案C：在地下设置城市轨道交通线路，在铁路车站正下方设站，并在铁路车站地下换乘大厅设置进出口；在站前广场旁设公交停车场，在广场前道路旁设公交停靠站。

3.1 评价指标计算

假设：①旅客站台上位置的分布随机；②铁路与市内公共交通之间的双向换乘客流大小相等。

根据前述计算方法，结合专家打分，得到数据如表1所示：

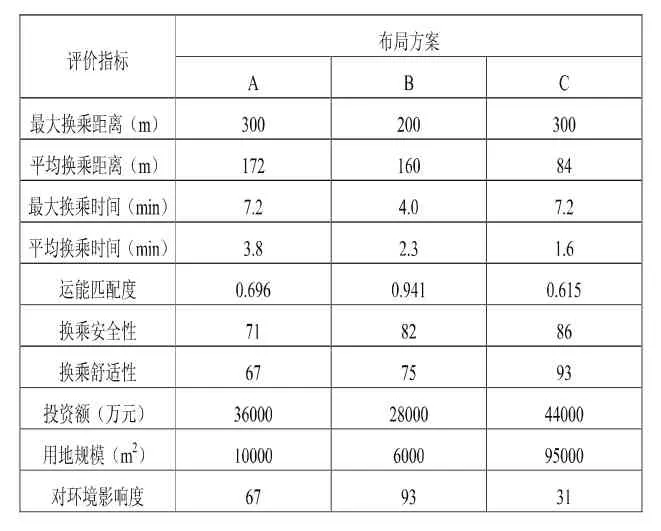
表1各方案评价指标计算结果

3.2 应用集对分析对各方案进行评价

依据上表，建立决策矩阵H：

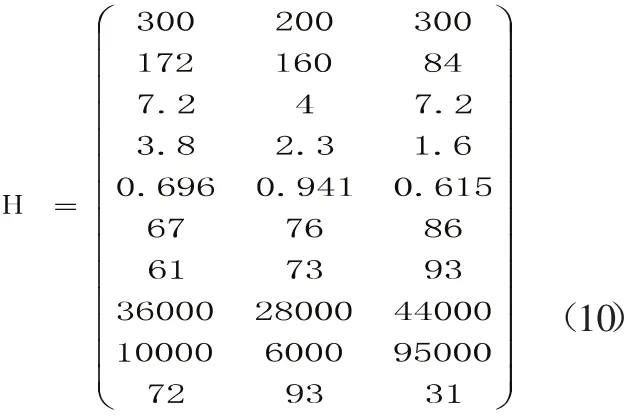
显然，可以得到理想方案

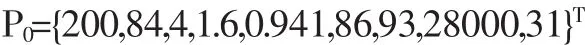
同一度矩阵Q

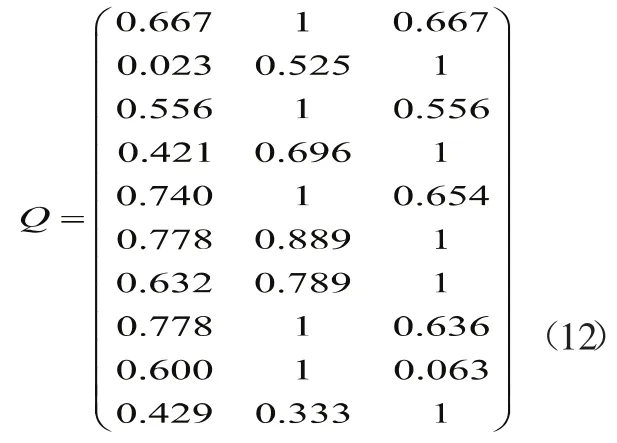
根据专家判断打分，计算得出判断矩阵的特征向量W。

最大特征根λmax=10.6748，

随机一致性比率CR=0.05042＜0.1，满足一致性要求。由此，可以计算得出设计方案与理想方案的带权同一度矩阵R：

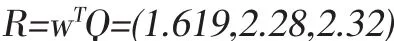
得到方案优劣排序为：方案A＜方案B＜方案 C。因此方案C为最优方案。

4 结束语

本文在区域公交化旅客运输换乘设施布局方案研究中，基于集对分析原理，建立了综合评价指标体系，确定了各指标的取值、权重的计算方法，构建了统一度决策矩阵，实现了定量与定性指标的综合，解决了各指标量纲不统一的问题，降低了主观评判的不确定性，并避免了复杂的建模及计算等，具有一定的可行性和可靠性。本文通过计算比较发现，在区域公交化旅客运输换乘设施布局中，将在铁路车站正下方设轨道交通车站、在站前广场旁设公交停车场、在广场前道路旁设公交停靠站较为合理。