δ-John域上共轭P-调和类型张量的Hardy-Littlewood积分估计

徐秀娟，刘晓丽

(河北联合大学理学院，河北唐山 063009)

0 引言

类似于对A-调和方程解的积分性质的研究，Ding和Bao等人对p-调和类型方程解的积分性质进行了深入研究，得到p-调和类型方程解的局部积分估计［1］。由于局部区域在具体问题的应用中有其局限性，所以研究问题的全局性已经成为人们所研究的重点内容之一。在文献［2］中Nolder给出了共轭A-调和张量局部的Hardy-Littlewood积分不等式，并且将其推广到δ-John域上，得到了全局Hardy-Littlewood积分不等式。本文在此基础上，利用δ-John域的性质和Whitney覆盖，通过选择适当的bQ，得到了δ-John域上p-调和类型方程A(x，a+du)=b+d*v的Hardy-Littlewood不等式。

1 基本概念与引理

定义［2］:如果Ω是Rn的一个子域，δ＞0，存在一个点x0∈Ω，可以通过一条连续曲线γ⊂Ω将任意Ω中的点x连接起来且

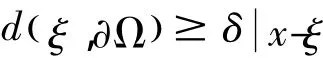
对任意ξ∈γ成立，这里dξ，∂()Ω是ξ和∂Ω之间的欧几里德距离，那么称Ω是一个δ-John域。

引理1.1［2］设Ω⊂Rn是一个δ-John域，那么存在一个Ω中的开覆盖ν，使得:

(2)存在一个特定的立方体Q0∈ν(称为中心立方体)，可以与ν中任一个立方体Q通过ν中立方体Q0，Q1，…，Qk=Q连接起来，使得对每一个i=0，1，…，k-1，有Q⊂NQi，且存在立方体R⊂Rn(这个立方体不需要在ν中)有下式成立:

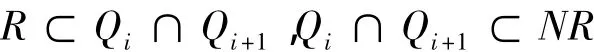
引理1.2［3］设u∈D(Ω，∧0)，v∈D(Ω，∧2)是p-调和类型方程A(x，a+du)=b+d*v的一组解，给定a，()b∈LpΩ，∧()l×LqΩ，∧()l，σ＞1是任意的常数，则存在与a，b，u，v无关的常量C，对于所有满足Q⊂σQ⊂Ω的立方体Q，及对任意的0＜s，t＜∞，满足:

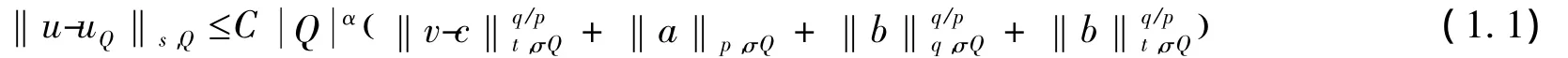
这里c∈Ω，()∧满足d*c=0，α=

引理1.3［2］对于任意一个Ω⊂Rn，存在一个动态的方体型的Whitney覆盖W=满足:

对所有的x∈Rn和某一N＞1成立，并且当Qi∩Qj≠∅时，存在一个方体R(∉W)属于Qi∩Qj使得Qi∩Qj⊂NR。另外，如果Ω是一个δ－John域，那么有一个特殊的方体Q0∈W，能与任何一个方体Q∈W用W中的一个方体链Q0，Q1，…，Qk=Q连接，使得Q⊂ ρQi， (i=0，1，…，k)，对某一个 ρ=ρ(n，δ)成立。

引理1.4［2］令0＜s＜∞，Ω是一个δ－John域，W是引理1.3中的一个Ω的Whitney分解，u∈D(Ω ，∧0)是一个广义的函数，如果对于任意的方体Q∈W都存在一个常数bQ使得:

那么存在一个仅与s，n和ρ有关的常数C，使得:

2 主要结果

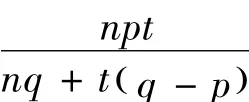
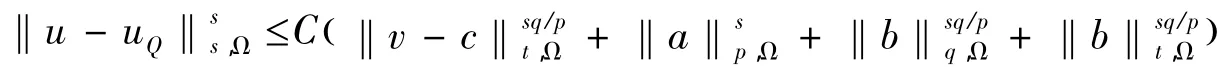
其中c∈Ω，()∧且d*c=0

证明:因为u∈DΩ，∧()0，v∈DΩ，∧()2是p－调和类型方程的一组解，所以由引理1.2可得:

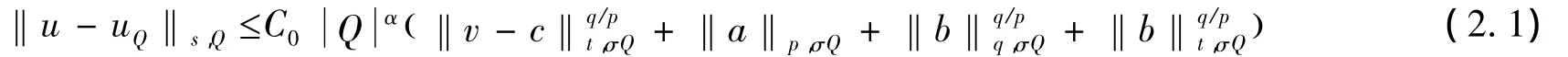
当s=φ()t时，对(2.1)式两边进行s次方，得到:

当0＜s＜1时，由基本不等式，得到:

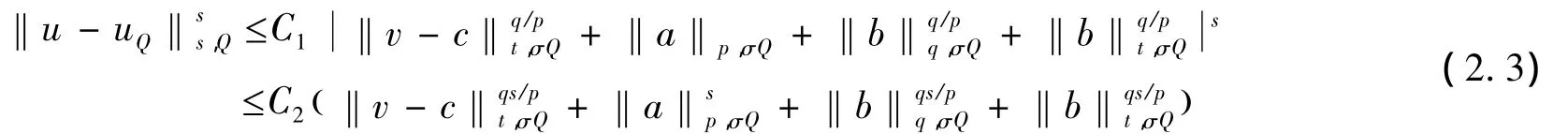
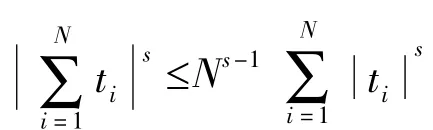
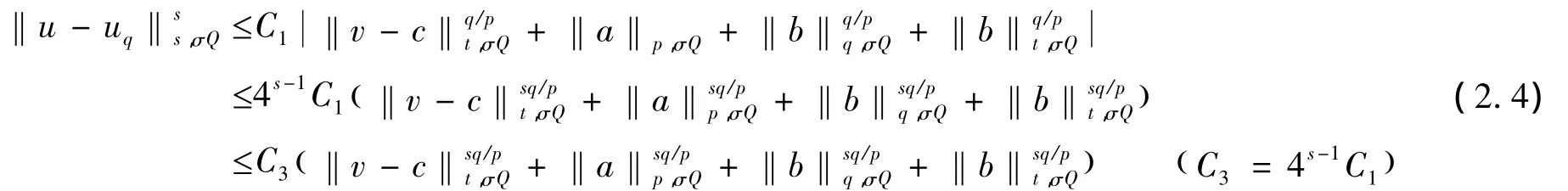
当σ=时，由(2.3)和(2.4)式知，当时，应用引理1.4得到:

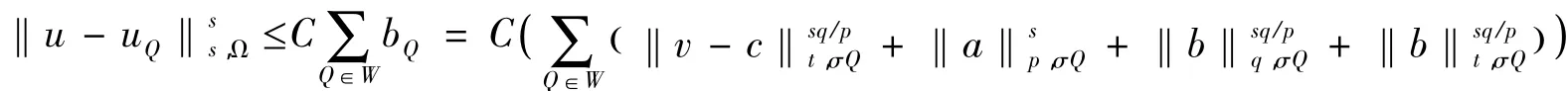
从而当s=φ()t，q≤p时，有qs/pt≥1，因此

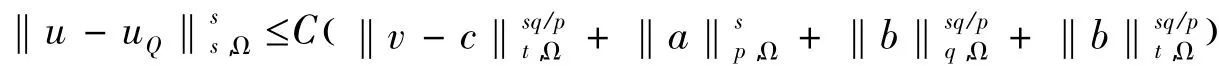
证毕

［1］L.D’Onofrio，T.Iwaniec.The P-harmonic transform beyond its natural domains of Definition［J］.Indiana Univ.math.2004，53(3):683-718.

［2］C.A.Nolder.Hardy-Littlewood Theorems for A-harmonic Tensors［J］.Illinois J.Math.1999，4(43):613-632.

［3］Z.Cao，G.Bao and R.Li.The Hardy-Littlewood Inequality for the Solution to P-harmonic Type System［J］.Mathematical Inequality and Application.2010.

［4］高红亚，张昱.A-调和张量的双权积分不等式.河北大学学报(自然科学版).2008，28(2):124-129.

［5］李娟.微分形式的双权积分不等式［J］.数学物理学报.2007，27A(3):515-523.