汽车轮胎冲上台阶力学过程分析

贾常明

（中国刑警学院 辽宁 沈阳 110035）

汽车轮胎冲上台阶力学过程分析

贾常明

（中国刑警学院 辽宁 沈阳 110035）

运用力学模型分析汽车前轮冲上台阶的过程，讨论轮胎冲上和跳离台阶时车速与台阶高度的关系，得出一般车速下轮胎都会冲上和跳离台阶，并结合实验对模型的局限性进行了分析。

交通事故 力学模型

建立“模型”是物理学研究中的典型方法。通过建立模型得出的规律虽是在理想化条件下得出的，但针对实际问题也有指导意义。在交通事故过程分析中，往往也可通过“力学模型”进行定性分析，但必须要结合实际情况进行修正。

1 力学模型

首先考虑单个轮胎的情况，令其半径为R，质量为m，以角速度ω0在水平地面作纯滚动，在前进的路上撞在一个高度为h的台阶上。设碰撞是完全非弹性的，即碰撞后轮胎不弹回。我们要研究的是轮胎能够翻上台阶而又始终不跳离台阶的情况下，对台阶的高度有什么要求。

这里把轮胎看成一均质圆盘（刚体），质心向右速度为v10，无滑滚动角速度为ω10，台阶给圆盘作用力为N，且碰撞点A不弹回，碰撞后角速度为ω1。轮胎碰撞台阶过程可分两步：碰撞过程和上升过程。

1.1 碰撞过程

运用角动量守恒定律可得

由转动惯量的平行轴定理可得

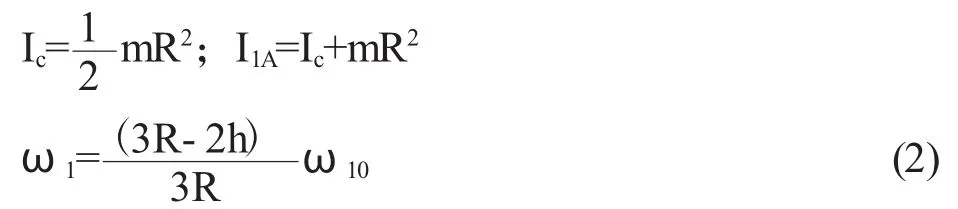
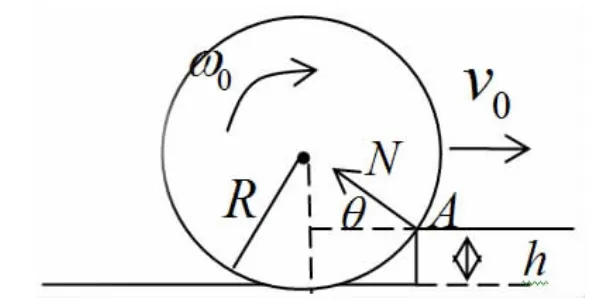
图1 轮胎冲撞台阶

1.2 上升过程

运用机械能守恒定律可得轮胎翻上台阶的角速度范围，即

轮胎不跳离台阶的条件是台阶的支撑力N大于0，从而求得轮胎不跳离台阶的角速度范围，即

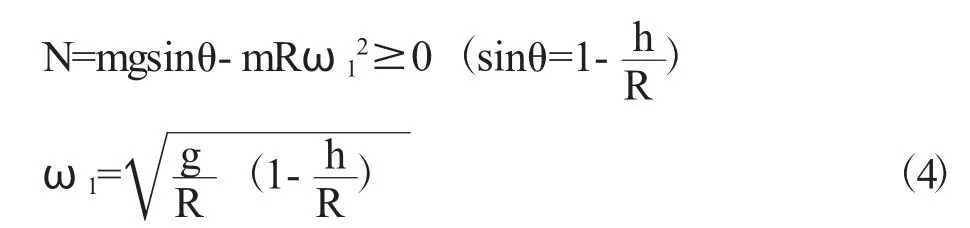
从公式（2）中可以看出，碰撞后的角速度ω1与轮胎质量m无关；h小于R时才有可能。

2 实际问题

在实际发生的交通事故中，存在汽车冲向一个台阶引发的事故。然而该过程中汽车前轮不能单纯简化为一个圆盘，因为轮胎的“轴”不但承担重量，还要承担整车向前的“惯性”。我们设汽车是自由冲向台阶，即驾驶员既没有“给油”也没有刹车。汽车前轮等效一个圆盘，质量为m，半径为R；另外整车给前轮的作用等效为在圆盘中心加上质量M，则有

图2 汽车前轮撞上台

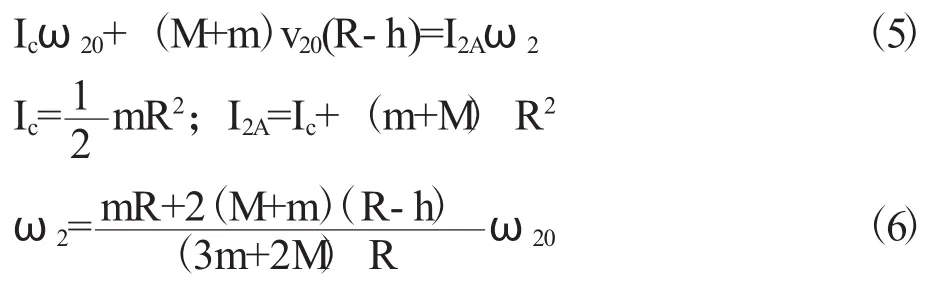
从公式（6）中可以看出，碰撞后的角速度ω2与质量M有关；h只能小于R。参考公式（3）可得汽车前轮滚上台阶的临界角速度范围，即

参考公式(4)可得汽车前轮不跳离台阶的角速度范围，即

令R=0.30m；h=0.04—0.30(m)；m=30kg；M=400kg。由于v10=Rω10，v20=Rω20，由公式（3） 和公式（7）得出轮胎和汽车前轮翻上台阶的临界车速v10，v20；由公式（4）和公式（8）可求得轮胎和汽车前轮跳离台阶的临界车速v11，v21，见表。v10和v11比较关系曲线见图3。

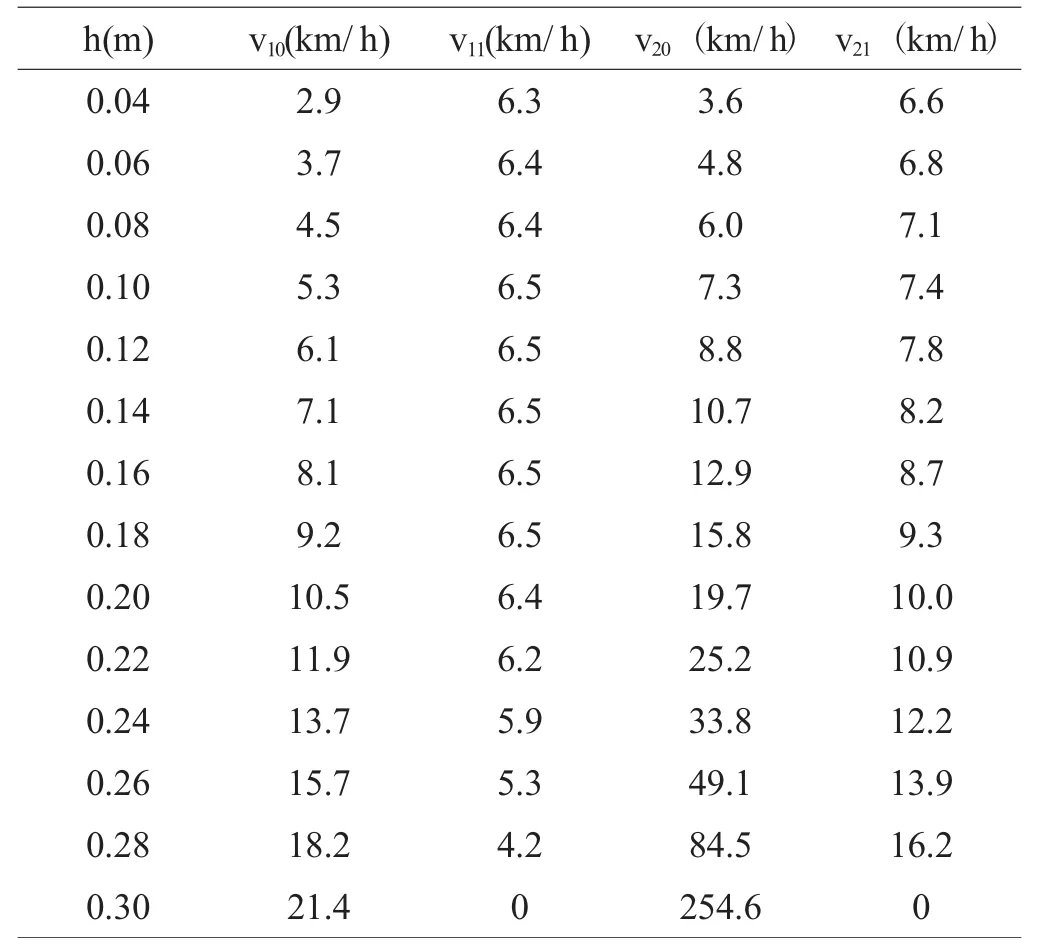
表 v10，v11，v20，v21与h的关系

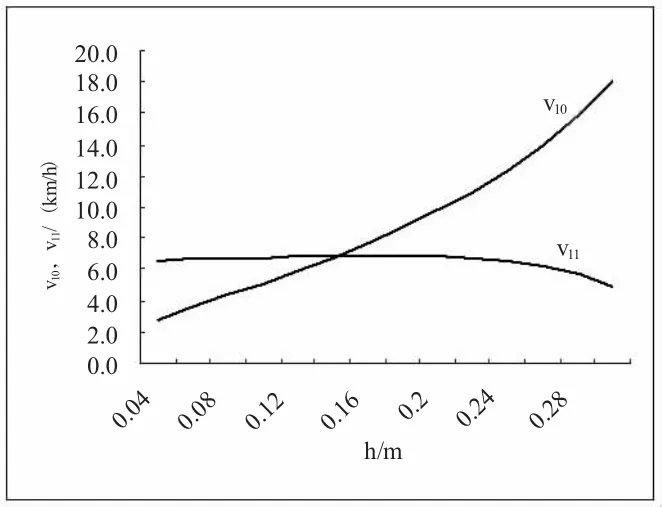
图3 v10和v11与h关系曲线比

3 实验研究

我们用轿车轮胎（R=30cm，m=8.5kg）冲撞不同高度（5cm；10cm；15cm；20cm）台阶。轮胎先弹起，质心做斜上抛运动，同时绕质心旋转，如图4中虚圆所示。初速度v0小时，轮胎弹起后没有跳上台阶，落下时转过一定角度，B点可能又与台阶尖角二次碰撞。初速度v0大时，轮胎弹起后转过一定角度跳上台阶。且初速度v0大，跳的远些；台阶高度大，跳的高些。

针对一定高度h，是否会有初速度v0取某一值时，使质心正好升高h，同时质心水平运动到台阶边沿。理论分析和实验表明这种情况几乎不可能，加上碰撞过程损失一点能量，如果轮胎要翻上台阶，初速度v0比理论值要大，跳的也要比h高。

由于轮胎的旋转作用，接触点A除有支撑力外，还有切向作用力，所以台阶给轮胎的作用力N的指向并非圆心，而是偏上，如图4所示。其作用效果使轮胎容易翻上台阶。

图4 轮胎冲撞台阶示意图

4 讨论

（1） v10和v20比较，汽车前轮翻上台阶临界速度要大一些；v11和v21的比较，汽车前轮跳离台阶临界速度也要大一些。

（2）v10和v11的比较，在h≤0.13(m)时（速度为6.5km/h），存在轮胎既翻上台阶又不跳离台阶的可能；h＞0.13(m)时，不存在既翻上台阶又不跳离台阶的情况，即翻上台阶就要跳离台阶。

（3）实际上轮胎翻上台阶又不跳离台阶是不存在的，因为碰撞并非完全非弹性碰撞，在轮胎“刚度”比较大情况下，碰撞时间较轮胎翻上台阶时间短，所以轮胎先弹起后，由于初速度大小不同，可能跳上台阶，也可能没跳上台阶。但实际车辆的前轮由于承重比较大，碰撞时间较轮胎翻上台阶时间长许多时，可以看成完全非弹性碰撞，从而轮胎是滚上而没跳起。

5 结论

从以上的力学模型计算结果可以得出，行驶中汽车前轮翻上“台阶”都要跳离。由于车速和汽车的减震情况不同，有可能引起不同后果，如车轮爆胎，严重情况可能引起翻车。

6 应用案例

6.1 案情简介

图5、图6是一起酒后驾驶车辆发生事故的现场照片，左前轮斜向冲向台阶，轮胎爆胎，整车向右侧翻倒，四轮朝天。针对该起交通事故，需要鉴定谁是驾驶员。

图5 轿车轮胎冲撞台阶痕迹图

图6 轿车翻车现场照片

6.2 案件分析

经事故现场调查，事故车辆驾驶员由于酒后驾驶，到达路口（中间有转盘）未及时右转，左前轮斜向冲向条石（高22cm），左前轮轮胎爆胎且在条石上滚动约“12米”后向右侧翻车。

该事故过程如图7所示。

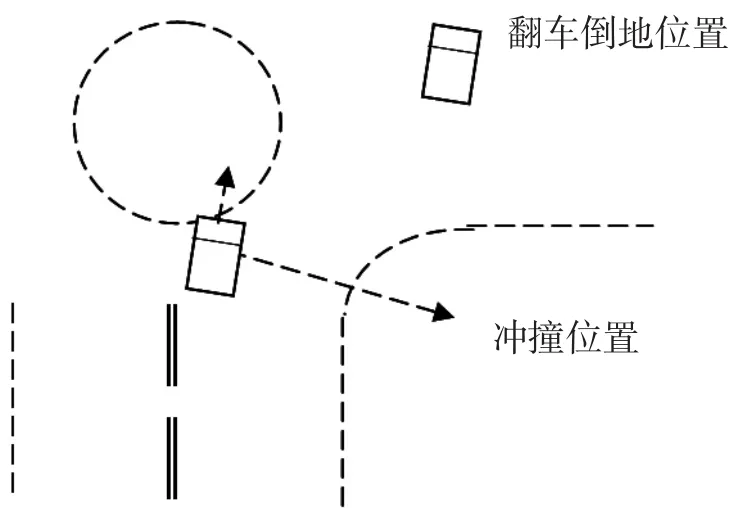
图7 事故车辆冲撞过程示意图

事故车辆冲撞路口中间转盘边缘条石瞬间，左前轮受力分析如图8所示。

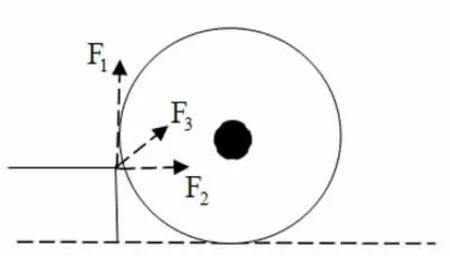
图8 事故车辆左前轮冲撞时作用力

图9 图6中照片的上下反转

左前轮受到向上作用力F1、向后作用力F2、向右作用力F3。由于F3作用在导向轮的前部，导致事故车辆右转，这样驾驶员和坐在副驾驶的乘员相对车辆有向左前方运动的可能。所以图中死者家属提出“死者”可能坐在副驾驶位置上。

将图6中的图片上下反转后如图9所示，驾驶员一侧的车门下部变形为F1作用形成，同时引起车辆左前部上下跳动，并造成车辆向右侧翻车。图中死者头部伸出门外可能是在车辆左前部上下跳动过程中形成的，非翻车过程中形成。

鉴定真假司机往往需要几方面信息点相互认证，如力学、痕迹、物质检验（血、毛发、纤维等）等。由于委托鉴定时“现场信息”一定程度上被破坏或丢失，单纯根据一方面得出的结论不易被信服。

1.赵凯华，罗蔚茵.新概念物理教程·力学[M].北京：高等教育出版社，1995

2.余志生.汽车理论[M].北京：机械工业出版社，2000

3.林洋.实用汽车事故鉴定学[M].黄永和，译.北京：人民交通出版社，2001

注：本文系国家自然科学基金项目阶段性研究成果之一，项目编号：61071057。